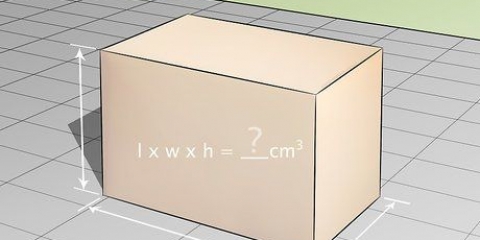
Suponha em nosso exemplo, que a massa de 10 kg está pendurada em uma corda, que não está presa a uma viga, mas é usada para levantar a massa com uma aceleração de 1 m/s. Em casos como este, temos que levar em conta não apenas a aceleração da massa, mas também a força gravitacional, resolvendo isso da seguinte forma: ft = Fg + m × a ft = 98 + 10 kg × 1 m/s ft = 108 Newtons. 
Como a direção e a magnitude da força centrípeta mudam à medida que o objeto na corda se move e a velocidade muda, o mesmo acontece com a tensão total na corda, que sempre puxa paralelamente à corda em direção ao ponto central. Lembre-se que a constante gravitacional puxa o objeto. Então, se um objeto é jogado em uma posição vertical, então a tensão total é a maior na parte inferior da trajetória do objeto (no caso de um relógio de pêndulo, isso também é chamado de equilíbrio), onde o objeto se move mais rápido. A tensão é menor no topo do movimento circular, onde a velocidade é mais baixa. Suponha no exemplo que o objeto balança como um pêndulo. A corda tem 1,5 metros de comprimento e a massa se move a uma velocidade de 2 m/s no ponto mais baixo. Se quisermos calcular a tensão nesse ponto, o ponto em que a velocidade é mais alta, devemos primeiro ver que a tensão devido à gravidade nesse ponto é a mesma de quando o pêndulo está em repouso - 98 Newtons. Para encontrar a força centrípeta, calculamos da seguinte forma: fc = m × f/r fc = 10 × 2/1.5 fc =10 × 2,67 = 26,7 Newtons. Então, a tensão total é 98 + 26,7 = 124,7 Newtons. 
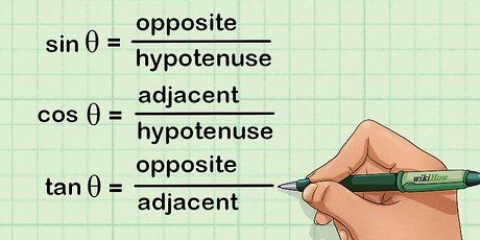
Quebrar a gravidade em dois vetores pode ajudá-lo a visualizar melhor esse conceito. Em qualquer ponto do arco de movimento de um objeto oscilante, a corda forma um ângulo de "θ" com a linha que passa pelo equilíbrio e o ponto central da rotação. À medida que a corda balança, você pode dividir a força da gravidade (m × g) em 2 vetores - mgsin(θ) é a tangente ao arco na direção do equilíbrio e mgcos(θ), o paralelo à força de tração no direção oposta. A tensão só precisa se opor a mgcos(θ) - a força que se opõe - não a força total da gravidade (exceto no ponto de equilíbrio, quando é igual à tensão). Suponha que o pêndulo forme um ângulo de 15 graus com a vertical e então tenha uma velocidade de 1,5 m/s. Encontramos a tensão da seguinte forma: Estresse devido à gravidade (Tg) = 98cos(15) = 98(0,96) = 94,08 Newtons força centrípeta (Fc) = 10 × 1,5/1,5 = 10 × 1,5 = 15 Newtons Tensão total = Tg + fc = 94,08 + 15 = 109,08 Newtons. 
Suponha que a massa de 10 kg não balance mais, mas seja arrastada horizontalmente no chão e em uma corda. Agora dizemos que o solo tem um coeficiente de atrito cinético de 0,5 e que a massa está se movendo com velocidade constante, mas queremos acelerá-la a 1 m/s. Essa nova atribuição revela duas mudanças importantes – a primeira é que não precisamos mais calcular a tensão devido à gravidade, porque a corda não suporta mais a massa e neutraliza a força. Agora temos que levar em conta a força de atrito e a tensão resultante, bem como a tensão causada pela aceleração do objeto. Resolvemos isso da seguinte forma: Força normal (N) = 10 kg × 9.8 (aceleração por gravidade) = 98 N Força de atrito cinético (Fr) = 0.5 × 98 N = 49 Newtons Força de aceleração (Fuma) = 10 kg × 1 m/s = 10 Newton Tensão total = Fr + fuma = 49 + 10 = 59 Newtons. 
Suponha que temos um sistema com massa de 10 kg (m1), conectado verticalmente, por meio de uma polia, com massa de 5 kg (m2) em uma inclinação de 60 graus (assumimos que a inclinação é sem atrito). Para encontrar a tensão na corda é mais fácil ser o primeiro a formular equações para as forças que aceleram as massas. Proceda da seguinte forma: A massa suspensa é mais pesada e não precisamos levar em conta o atrito, então sabemos que há uma aceleração para baixo. Mas a tensão na corda puxa a massa para cima, então calculamos a força resultante na corda da seguinte forma: F = m1(g) - T, ou 10(9.8) - T = 98 - T. Sabemos que a massa vai acelerar na encosta. Como a inclinação não tem atrito, sabemos que a tensão puxa a massa para cima da inclinação, retida apenas pela própria massa do peso. A componente da força que puxa o peso para baixo é calculada por mgsin(θ), então no nosso caso podemos dizer que o peso para cima acelera a inclinação pela força resultante F = T - m2(g)pecado(60) = T - 5(9.8)(.87) = T - 42.63. A aceleração das duas massas é a mesma, então temos (98 - T)/m1 = T - 42.63 /m2. Depois de alguma álgebra simples, obtemos T = 61.09 Newton. 
Suponha neste sistema em forma de Y, que o objeto tem um peso de 10 kg e que as duas cordas superiores fazem um ângulo com o teto de 30 graus e 60 graus. Se quisermos encontrar a tensão em cada uma das cordas superiores, temos que considerar os componentes vertical e horizontal da tensão para cada corda. As duas cordas neste exemplo ficam perpendiculares uma à outra, facilitando o cálculo dessas tensões, de acordo com as definições das funções trigonométricas. Então da seguinte forma: A razão entre T1 ou T2 e T = m(g) é igual ao seno do ângulo entre cada corda de suporte e o teto. para T1 é sin(30) = 0,5, enquanto para T2 sustenta que sin(60) = 0,87. Multiplique a tensão na corda inferior (T = mg) pelo seno de cada ângulo, para obter T1 e T2 encontrar. t1 =0,5 × m(g) =0,5 × 10(9,8) = 49 Newtons. t2 =0,87 × m(g) =0,87 × 10(9,8) = 85,26 Newtons.
Calculando forças em física
Contente
Na física, a tensão é a força exercida por uma corda, corda, cabo ou objeto semelhante em um ou mais outros objetos. Tudo o que é puxado fica suspenso, apoiado ou preso a uma corda.d. oscila, está sujeito à força de tração. Como outras forças, a tensão pode acelerar ou deformar objetos. Ser capaz de calcular a tensão é uma habilidade importante para estudantes de física, mas também para engenheiros e arquitetos. Afinal, para projetar edifícios seguros, eles devem saber exatamente se a tensão em um cabo pode suportar a carga de um objeto. Continue lendo na Etapa 1 para aprender a calcular o estresse em vários sistemas físicos.
Degraus
Método 1 de 2: Determinando a tensão em um único cordão

1. Determine as forças em cada lado do fio. A tensão em um dado cordão de uma corda é a soma de todas as forças que puxam a corda de ambas as extremidades. Não esqueça: força = massa × aceleração. Suponha que a corda esteja esticada firmemente, então qualquer mudança na aceleração ou massa dos objetos que a corda suporta causará uma mudança na tensão na corda. Esqueça a constante aceleração devido à gravidade nenhum - mesmo quando um sistema está em repouso, cada componente é exposto à gravidade. A tensão em uma corda particular pode ser expressa como T = (m × g) + (m × a), onde "g" a aceleração é devida à gravidade de qualquer objeto sustentado pela corda, e "uma" é qualquer outra aceleração em qualquer objeto suportado pela corda.
- Por uma questão de simplicidade, podemos supor que estamos lidando com umfio ideal – em outras palavras, que a corda, o cabo, etc. é fino e sem massa, e não pode esticar ou quebrar.
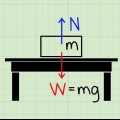
- Um exemplo: suponha que tenhamos um sistema onde uma massa pende de uma viga de madeira, presa com uma única corda (ver figura). Ainda as massas ainda movem a corda - todo o sistema está em repouso. Agora sabemos que a massa está em equilíbrio, onde a força de tração é igual à força gravitacional sobre a massa. Em outras palavras, a tensão (Ft) = Força ou Gravidade (Fg) = m × g.
- Suponha que temos uma massa de 10 kg, então vale o seguinte: tensão = 10 kg × 9,8 m/s = 98 Newtons.

2. Fique atento à aceleração. A gravidade não é a única força que afeta a tensão em uma corda - qualquer força pode ser associada à aceleração de um objeto ao qual a corda está conectada. Se um objeto pendurado é acelerado por uma força na corda ou no cabo, então a força causada pela aceleração (massa × aceleração) é adicionada à tensão causada pela massa do objeto.

3. Considere também uma engrenagem circular. Um objeto que é girado em torno de um ponto central em uma corda (como um pêndulo) exerce uma tensão na corda causada pela força centrípeta. A força centrípeta é a força que a corda exerce sobre um objeto puxando-o para dentro "Puxar", para que o objeto continue a se mover em um arco, em vez de ir direto. Quanto mais rápido o objeto se move, maior a força centrípeta. força centrípeta (Fc) é igual a m × v/r onde "m" é igual à massa, "v" é a velocidade e "r" é o raio do círculo, ou seja, o caminho no qual o objeto se move.

4. Entenda que a tensão devido à gravidade muda durante o período do pêndulo. Como mencionado anteriormente, tanto a direção quanto a magnitude da força centrípeta mudam à medida que um objeto oscila. Mas embora a gravidade permaneça constante, a tensão devido à gravidade também mudar. Como um objeto balançando não parte inferior do balanço do pêndulo (o ponto de equilíbrio), então a gravidade puxa para baixo, mas a tensão puxa o objeto em um ângulo. Por causa disso, a tensão cancelará parte da força gravitacional, mas não completamente.

5. Pense também no atrito. Qualquer objeto puxado por uma corda e experimentando atrito de outro objeto (ou líquido) transfere essa força de atrito para a tensão na corda. A força de atrito entre dois objetos é calculada da mesma forma que em qualquer outra situação – pela seguinte equação: Força por atrito Fr = (mu)N, onde mu é o coeficiente de atrito entre os dois objetos e onde N é a força normal entre os dois objetos (a força com a qual eles pressionam um contra o outro). Observe que o atrito estático – o atrito que ocorre quando você tenta mover um objeto estacionário – é diferente do atrito cinético – o atrito que ocorre quando você tenta manter um objeto em movimento em movimento.
Método 2 de 2: Calculando a tensão em vários acordes

1. Elevação de cargas verticais paralelas com uma polia. Uma polia é uma máquina simples que consiste em uma roda suspensa que permite que a força de tensão em uma corda mude de direção. Em uma configuração simples, a corda ou cabo vai de uma massa pendurada até a polia, depois desce para outra massa, dando-lhe dois comprimentos de corda. Mas a tensão em ambas as partes da corda é a mesma, mesmo se massas de tamanhos diferentes pendem de ambas as extremidades da corda. Em um sistema de duas massas suspensas por uma polia, a tensão é igual a 2g(m1)(m2)/(m2+m1), através do qual "g" a aceleração é devido à gravidade, "m1" a massa do objeto 1 e "m2" a massa do objeto 2. Observe que, como uma massa é mais pesada que a outra, o sistema irá acelerar, com os 10 kg descendo e os 5 kg subindo.
- Observe que assumimos um "polia ideal – sem massa, sem atrito e polias que não podem quebrar, deformar ou soltar do teto.
- Suponha que temos duas massas penduradas em uma polia, em cordas paralelas. O peso 1 tem massa de 10 kg e o peso 2 tem massa de 5 kg. Neste caso, encontramos a tensão da seguinte forma:
- T = 2g(m1)(m2)/(m2+m1)
- T = 2(9,8)(10)(5)/(5 + 10)
- T = 19,6(50)/(15)
- T = 980/15
- T = 65,33 Newtons.
2. Levantar pesos com uma polia em cordas verticais, mas não paralelas. As polias são frequentemente usadas para obter tensão em uma direção diferente de cima ou para baixo. Por exemplo, se uma massa está pendurada verticalmente em uma extremidade da corda, enquanto uma segunda massa está amarrada em um declive na outra extremidade, esse sistema de polias não paralelas tomará a forma de um triângulo cujos vértices são a primeira massa, a segunda massa e a própria polia. Neste caso, a tensão no cabo é determinada tanto pela gravidade sobre a massa quanto pela componente da força de tração que atua paralelamente à porção diagonal do cabo.

3. Usando vários cabos para pendurar um objeto. Finalmente, consideramos o caso em que um objeto está pendurado em um "em forma de Y" sistema de cordas – duas cordas são presas ao teto e se encontram em um ponto central, onde um peso pende de uma terceira corda. A tensão na terceira corda é óbvia - esta é simplesmente a tensão resultante devido à gravidade. As tensões nas outras duas cordas são diferentes e, quando somadas, devem ser iguais à gravidade na direção ascendente e vertical, e iguais a zero na direção horizontal (assumindo que o sistema está em repouso). A tensão nas cordas é afetada pela massa do objeto pendurado, bem como pelo ângulo de cada corda em relação ao teto.
Artigos sobre o tópico "Calculando forças em física"
Оцените, пожалуйста статью
Similar
Popular