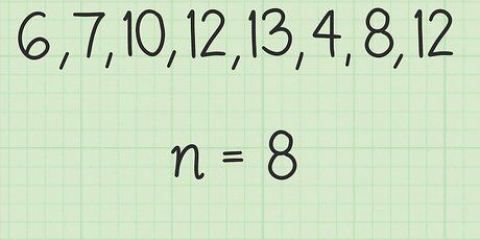Calculando o Intervalo de Confiança: 6 Passos (com Imagens)

Contente

Degraus
Pontas
Necessidades

O intervalo de confiança é um indicador da precisão de suas leituras. Também indica a estabilidade da sua estimativa; o grau em que suas leituras correspondem à sua estimativa se você repetir o experimento. Siga as etapas abaixo para calcular o intervalo de confiança para seus dados.

Degraus

Imagem intitulada Calcular Intervalo de Confiança Passo 1

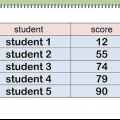
1. Anote o fenômeno que você deseja testar. Suponha que você trabalhe com a seguinte situação: O peso médio de um estudante universitário masculino A é de 180 libras. Agora você testará como exatamente pode prever o peso dos estudantes do sexo masculino na universidade A usando um determinado intervalo de confiança.

Imagem intitulada Calcular Intervalo de Confiança Passo 2

2. Pegue uma amostra da sua população escolhida. Isto é o que você usará para coletar os dados para testar sua hipótese. Suponha que você tenha escolhido 1000 alunos aleatórios.

Imagem intitulada Calcular Intervalo de Confiança Passo 3

3. Calcular a média amostral e o desvio padrão. Escolha uma amostra (ou seja, a média amostral e o desvio padrão) que você deseja usar para a estimativa do parâmetro populacional escolhido. Um parâmetro populacional é uma certa característica da população. Aqui está a média amostral e o desvio padrão:

Para calcular a média amostral dos dados, some todos os pesos dos 1.000 homens selecionados e divida o resultado por 1.000, o número de homens. A média neste exemplo é de 180 libras.

Para calcular o desvio padrão, você precisará calcular a média dos dados. Agora é necessário calcular a variância dos dados, também conhecida como a média do quadrado das diferenças da média. Depois de encontrar esse número, subtraia sua raiz quadrada. Suponha que o desvio padrão seja 30 libras. (Às vezes isso é dado com uma tarefa.)

Imagem intitulada Calcular Intervalo de Confiança Etapa 4

4. Escolha o nível de confiança que você deseja. Os níveis de confiança mais usados são 90%, 95% e 99%. Também é possível que isso seja dado com uma tarefa. Suponha que você tenha escolhido 95%.

Imagem intitulada Calcular Intervalo de Confiança Passo 5

5. Calcule a margem de erro. Você pode encontrar a margem de erro usando a seguinte fórmula: z_a/2 * σ/√(n).z_a/2 = coeficiente de confiança, onde a = nível de confiança, σ = desvio padrão e n = tamanho da amostra. Esta é outra maneira de indicar que você precisa multiplicar o valor crítico pelo erro padrão.Você resolve a fórmula da seguinte forma, dividindo-a:

Determine o valor crítico, Z_a/2: O nível de confiança é de 95%. Converta essa porcentagem para um decimal, 0,95, e divida por 2 para obter 0,475. Então veja no próximo tabela z para encontrar o valor correspondente a 0,475. O valor mais próximo é 1,96, na interseção da linha 1,9 e coluna 0,06.

Para encontrar o erro padrão, pegue o desvio padrão 30 e divida-o pela raiz quadrada do tamanho da amostra (1000). Agora você obtém 30/31,6 = 0,95 libras.

Multiplique 1,96 por 0,95 (o valor crítico vezes o erro padrão) e você obtém 1,86 ou a margem de erro.

Imagem intitulada Calcular Intervalo de Confiança Etapa 6

6. Agora indique qual é o intervalo de confiança. Para fazer isso, pegue a média (180) e anote-a ao lado do ± e da margem de erro. A resposta é: 180 ± 1,86. Você pode encontrar os limites superior e inferior do intervalo de confiança adicionando e subtraindo a margem de erro da média. Portanto, o limite inferior é 180 – 1,86 ou 178,14, e o limite superior é 180 + 1,86 ou 181,86.

Você também pode usar a seguinte fórmula útil para encontrar o intervalo de confiança: x̅ ± Z_a/2 * σ/√(n). Aqui x̅ representa a média.

Pontas

Tanto o t-score quanto o z-score podem ser calculados manualmente, com uma calculadora ou com tabelas estatísticas. Os escores Z também podem ser determinados com a Calculadora de Distribuição Normal e os escores t com a Calculadora de Distribuição t. Ferramentas online também estão disponíveis.
A população da amostra deve ser normal para um intervalo de confiança correto.
O valor crítico usado para calcular a margem de erro é uma constante expressa como t-score ou z-score. Os escores T são geralmente preferidos em relação ao desvio padrão da população é desconhecido ou quando uma amostra pequena é usada.
Existem muitos métodos, como amostra aleatória, amostra sistemática e amostra estratificada, que permitem obter uma amostra representativa para usar no teste de hipóteses.
Um intervalo de confiança não diz nada sobre a probabilidade de um determinado resultado. Por exemplo, se você tem 95% de certeza de que a média da sua população está entre 75 e 100, o intervalo de confiança de 95% não significa que há uma chance de 95% de que a média esteja dentro do intervalo calculado.