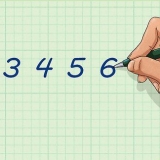Cálculo de Proporção: 7 Passos (com Imagens)

Contente

Degraus
- Parte 1 de 2: Escrevendo uma proporção
- Parte 2 de 2: Usando proporções em problemas de matemática
Exercícios de exemplo
Pontas
Necessidades

Proporções ou razões são expressões matemáticas que comparam dois ou mais números. As proporções podem comparar quantidades e números fixos ou pode ser usado para comparar partes do todo. As proporções podem ser calculadas e anotadas de maneiras diferentes, mas os princípios são os mesmos para todos os rácios. Veja a Etapa 1 abaixo para começar com proporções.

Degraus

Parte 1 de 2: Escrevendo uma proporção

Imagem intitulada Calcular Proporções Etapa 1

1. Entenda como as proporções são usadas. Os relacionamentos são encontrados em todos os lugares, no mundo científico ou em casa. As razões mais simples comparam apenas dois valores, mas é claro que mais também é possível.

Um exemplo: em uma turma com 20 alunos, dos quais 5 meninas e 15 meninos, podemos expressar o número de meninas e meninos como uma proporção.

Imagem intitulada Calcular Proporções Etapa 2

2. Escreva uma proporção com dois pontos. Uma maneira comum de indicar uma proporção é com dois pontos entre os números. Se você comparar dois números, escreva, por exemplo, como 7 : 13 e se houver 3 ou mais números, por exemplo, da seguinte forma 10 : 2 : 23.

Assim, em nossa sala de aula, podemos escrever a proporção de meninas para meninos da seguinte forma:5 meninas: 15 meninos. Opcionalmente, você pode omitir a designação, desde que se lembre do que a proporção significa.

Imagem intitulada Calcular Proporções Etapa 3

3. Uma razão é o mesmo que uma fração e, portanto, pode ser simplificada. Você faz isso dividindo todos os termos da razão pelos divisores comuns, até que não haja mais divisores comuns. Mas quando você faz isso, é importante não esquecer quais eram os números originais da razão. Ver abaixo.

No exemplo da sala de aula, havia 5 meninas e 15 meninos. Ambos os lados da razão são divisíveis por 5. Isso permite que você simplifique a proporção para1 menina: 3 meninos.

Mas não devemos perder de vista os números originais. Não há 4, mas 20 alunos no total na classe. A razão simplificada apenas compara a relação entre o número de meninos e meninas. Há 3 meninos para 1 menina na proporção ou fração, não 3 meninos e 1 menina na classe.

Algumas proporções não podem ser simplificadas. Por exemplo, 3 : 56 não pode ser simplificado porque os 2 números não têm fatores iguais - 3 é primo e 56 não é divisível por 3.

4. Existem também métodos alternativos para escrever proporções. Embora os dois pontos sejam talvez o mais fácil para escrever proporções, existem outras maneiras que não afetam a proporção. Ver abaixo:

As proporções também podem ser exibidas como "3 fica para 6" ou "11 em 4 em 20".

Você também pode escrever proporções como uma fração. Muitas vezes o uso de ambos os termos leva a alguma confusão, mas frações são proporções e vice-versa. Então você também pode escrever uma proporção com uma linha de divisão. Por exemplo, a razão 3/5 e a fração 3/5 não diferem entre si. Como no exemplo da turma: eram 3 meninos para cada menina, uma proporção de 1:3, mas como fração expressa a mesma coisa, ou seja, 1/3 do total de alunos é menina.

Parte 2 de 2: Usando proporções em problemas de matemática

1. Use a multiplicação ou divisão para alterar as proporções sem alterar a proporção. Multiplicar ou dividir ambos os termos de uma razão por um determinado número produz a mesma razão, mas com números maiores ou menores.

Por exemplo, suponha que você seja um professor e lhe peçam para aumentar o tamanho da turma 5 vezes, mas com a mesma proporção de meninos e meninas. Se há 8 meninas e 11 meninos na classe agora, quantos estão na nova classe??Leia a solução:

8 meninas e 11 meninos, então uma proporção de 8: 11. Essa proporção indica, portanto, que, independentemente do tamanho da turma, há 8 meninas para 11 meninos.
(8: 11) × 5
(8×5: 11×5)
(40:55). A nova classe consiste em 40 meninas e 55 caras - 95 alunos no total!

Imagem intitulada Calcular Proporções Etapa 4

2. Use a multiplicação cruzada para encontrar a variável desconhecida, ao trabalhar com duas razões equivalentes. Outro problema bem conhecido é quando você é solicitado a calcular a incógnita de uma razão. A multiplicação cruzada torna isso muito fácil. Escreva cada razão como uma fração, torne-as iguais e multiplique transversalmente para resolver.

Como exemplo, digamos que temos um grupo de alunos de 2 meninos e 5 meninas. Se quisermos manter a proporção intacta, quantos meninos há em um grupo de 20 meninas?Para resolver isso, fazemos duas razões, uma com a variável desconhecida: 2 meninos: 5 meninas = x meninos: 20 meninas. Na forma de fração fica assim: 2/5 = x/20. Use a multiplicação cruzada para resolver isso. Ver abaixo:

2/5 = x/20

5 × x = 2 × 20

5x = 40

x = 40/5 = 8. Então, há 20 meninas e 8 caras.

3. Use razões para encontrar quantidades desconhecidas, onde outra é dada. Se você estiver lidando com uma variável que determina a relação entre várias quantidades, das quais 1 ou mais são desconhecidas, você pode encontrar o valor de cada incógnita usando apenas uma quantidade conhecida. Muitas vezes, esses tipos de declarações envolvem o cálculo das quantidades de ingredientes em uma receita. Para encontrar as quantidades desconhecidas, divida o termo conhecido da razão pela quantidade dada; compartilhe depois cada termo na razão pela resposta que você recebe. Um exemplo deixará tudo um pouco mais claro:

Suponha que nossa classe esteja assando biscoitos como uma tarefa. Se a receita da massa consiste em farinha, água e manteiga na proporção 20 : 8 : 4, e cada aluno recebe 5 xícaras de farinha; quanta água e manteiga cada aluno precisa? Para resolver isso, primeiro divida o termo da razão correspondente à razão conhecida (20) pela quantidade conhecida (5 xícaras). Em seguida, divida cada termo na razão pela resposta que você obtém para encontrar a quantidade exata para cada. Ver abaixo:

20/5 = 4

20/4: 8/4: 4/4

5 : 2 : 1. assim, 5 xícaras de farinha, 2 xícaras de água e 1 xícara de manteiga.

Exercícios de exemplo

Biscoitos são feitos de manteiga e açúcar na proporção de 5:3. Se forem usadas 7 partes de manteiga, quanto açúcar é necessário?

Para fazer isso, use a razão na forma de uma fração. Neste caso, tornamos um decimal - cerca de 1,67.
A fórmula está pronta para ser usada. Queremos encontrar a quantidade de açúcar, então vamos deixar para o que é e calcular a fração manteiga/1,67, então 7/1,67 = 4,192

A parte que trata das proporções é a divisão proporcional. Quando uma quantidade total é dividida em partes, uma proporção é criada. Por exemplo: Annemiek, Anna e Anton trabalham na loja da mãe. Annemiek trabalhou uma hora, Anna 3 e Anton 6 horas (portanto, uma proporção de 1:3:6). A mãe dá-lhes uma quantia total e pede-lhes que dividam na proporção certa. O valor total foi de 100€. Você faz isso somando as partes da proporção, para saber quanto vale cada parte. 1:3:6 então se torna 1+3+6=10 então $ 100/10 = $ 10 então agora sabemos que cada parte da razão vale $ 10... e é por isso que todos recebem um salário de € 10 por hora. Agora podemos usar isso para calcular o que cada um ganhou. Annemiek recebe € 10, Anna recebe € 30 e Anton recebe € 60. Verifique isso somando todos os salários, que devem sair para € 100. 10+30+60= 100. Correto!

Pontas

Simplifique as razões usando o botão ab/c em sua calculadora (isso é para escrever frações mistas e simplificar). Por exemplo, se você tem 8:12, você testa "8 ab/c 12" = in e você obtém 2/3 e, portanto, a proporção 2:3.