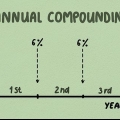
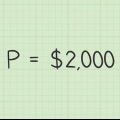O capital (P) é o primeiro valor depositado na conta ou o valor atual que você assume para fazer o cálculo dos juros. A taxa de juros (r) deve estar na forma decimal. Um juro de 3% deve ser inserido como 0,03. Para fazer isso, divida a taxa de juros especificada por 100. O valor de (n) é o número de vezes por ano que os juros são calculados e adicionados ao seu saldo (também conhecido como capitalização). Os juros geralmente são compostos mensalmente (n=12), trimestralmente (n=4) ou anualmente (n=1), mas pode haver outras opções dependendo das condições específicas da sua conta. 
Os juros compostos diários são determinados de maneira semelhante, exceto que você substituiria o 4 conforme usado acima para variável(s) por 365. 
Isso é ainda mais simplificado resolvendo o termo dentro dos parênteses,  . A equação agora fica assim:
. A equação agora fica assim:  .
. 
Observe que isso é um pouco maior do que  , que você poderia esperar ao enviar a taxa de juros anual. Isso ilustra a importância de entender como e quando seus juros são compostos!
, que você poderia esperar ao enviar a taxa de juros anual. Isso ilustra a importância de entender como e quando seus juros são compostos! Os juros são a diferença entre A e P, de modo que o total de juros compostos ganhos é  .
. 


O principal ou capital `P` representa o saldo da conta na data em que você inicia o cálculo. A taxa de juros `r` representa os juros pagos na conta a cada ano. Deve ser expresso como um número decimal na equação. Ou seja, uma taxa de juros de 3% é notada como 0,03. Você obtém esse número dividindo a porcentagem especificada por 100. O valor `n` representa o número de vezes que os juros são compostos anualmente. São 365 com uma diária, 12 mensais e 4 com juros compostos por trimestre. O valor para `t` representa o número de anos durante os quais você calcula os juros futuros. Este é o número de anos ou parte de um ano, se você assumir menos de um ano (por exemplo,. 0,0833 (1/12) por um mês). 









O recurso de `valor futuro` foi projetado para pagar antecipadamente um saldo de conta à medida que continua a acumular juros, em vez de acumular juros de poupança. Como resultado, ele retorna automaticamente um número negativo. Você pode combater esse problema digitando: 
A função TW recebe parâmetros de dados semelhantes, separados por vírgulas, mas não exatamente iguais. Por exemplo: `interesse` refere-se a  (a taxa de juros anual dividida por `n`). Isso calculará automaticamente os termos entre parênteses da função TW.
(a taxa de juros anual dividida por `n`). Isso calculará automaticamente os termos entre parênteses da função TW. O parâmetro `número de parcelas` refere-se à variável  o número total de parcelas sobre as quais o acúmulo é calculado e o número total de pagamentos. Em outras palavras, se o seu PMT não for 0, a função VA assumirá que você adiciona o valor do PMT em cada período, conforme definido pelo `número de parcelas`.
o número total de parcelas sobre as quais o acúmulo é calculado e o número total de pagamentos. Em outras palavras, se o seu PMT não for 0, a função VA assumirá que você adiciona o valor do PMT em cada período, conforme definido pelo `número de parcelas`. Observe que essa função geralmente é usada para (coisas como) calcular como o principal de uma hipoteca foi pago ao longo do tempo, por meio de pagamentos regulares. Por exemplo, se você planeja pagar todos os meses por cinco anos, o "número de parcelas" passa a ser 60 (5 anos x 12 meses). `Aposta` é a sua contribuição regular ao longo do período (uma contribuição por `n`) `[hw]` (valor atual) é o principal - o saldo inicial de sua conta. A última variável, `[type_number]` pode ser deixada em branco para este cálculo (nesse caso, a função a definirá automaticamente como 0). A função TW oferece a possibilidade de fazer alguns cálculos básicos dentro dos parâmetros da função, por exemplo, a função totalmente completa TW pode ser assim:  . Isso indica uma taxa de juros anual de 5% composta mensalmente por 12 meses, período em que você deposita $ 100/mês com um saldo inicial (principal) de $ 5.000. A resposta a esta função lhe dará o saldo da conta após 1 ano (€ 6.483,70).
. Isso indica uma taxa de juros anual de 5% composta mensalmente por 12 meses, período em que você deposita $ 100/mês com um saldo inicial (principal) de $ 5.000. A resposta a esta função lhe dará o saldo da conta após 1 ano (€ 6.483,70).
Calcular juros em uma conta poupança
Contente
Embora os juros dos depósitos de poupança às vezes sejam fáceis de calcular multiplicando a taxa de juros pelo saldo inicial, na maioria dos casos não é tão fácil. Por exemplo: muitas cadernetas de poupança indicam juros anualmente, mas calculam juros compostos mensalmente. A cada mês, uma fração dos juros anuais é calculada e adicionada ao seu saldo, o que, por sua vez, afeta o cálculo dos meses seguintes. Esse ciclo de juros, em que os juros são calculados em etapas e adicionados ao seu saldo continuamente, é chamado de juros compostos, e a maneira mais fácil de calcular o saldo futuro é usando uma fórmula de juros compostos. Continue lendo para aprender os prós e contras desses tipos de cálculos de juros.
Degraus
Método 1 de 3: Calcular juros compostos

1. Conheça a fórmula para calcular o efeito dos juros compostos. A fórmula para calcular a acumulação de juros compostos sobre um determinado saldo é:  .
.
 .
. - (P) é o capital, (r) é a taxa de juros anual e (n) é o número de vezes que os juros são compostos por ano. (A) é o saldo sobre o qual você calcula, incluindo os efeitos dos juros.
- (t) representa os períodos durante os quais os juros foram acumulados. Deve corresponder à taxa de juros que você está assumindo (por exemplo, se for juros anuais, então (t) deve ser um número de anos como uma fração). Para exibir o número correto de anos como uma fração em um período de tempo, divida o número total de meses por 12 ou divida o número total de dias por 365.

2. Determine as variáveis usadas na fórmula. Leia os termos e condições da sua conta privada ou entre em contato com um funcionário do seu banco para completar a comparação.

3. Insira seus valores na fórmula. Depois de determinar os valores de cada variável, você pode inseri-los na fórmula de juros compostos para determinar a taxa de juros na escala de tempo especificada. Por exemplo, com os valores P=1000, r=0,05 (5%), n=4 (compilado por trimestre) e t=1 ano, obtemos a seguinte equação:  .
.
 .
.
4. Faça o cálculo. Agora que os números foram inseridos, é hora de resolver a fórmula. Comece simplificando as partes simples da equação. Divida a taxa de juros anual pelo número de parcelas para obter a taxa de juros periódica (neste caso  ) e resolva o alvo
) e resolva o alvo  qual só aqui
qual só aqui  é. Isso resulta na seguinte equação:
é. Isso resulta na seguinte equação:  .
.
 ) e resolva o alvo
) e resolva o alvo  qual só aqui
qual só aqui  é. Isso resulta na seguinte equação:
é. Isso resulta na seguinte equação:  .
. . A equação agora fica assim:
. A equação agora fica assim:  .
.
5. Resolva a equação. Em seguida, resolva o expoente elevando o último degrau à potência de quatro (ou seja,  ). Isso entrega
). Isso entrega  como resultado em. A equação agora é:
como resultado em. A equação agora é:  . Multiplique esses dois números e você terá
. Multiplique esses dois números e você terá  . Este é o valor da sua conta com juros de 5% (compostos por trimestre) após um ano.
. Este é o valor da sua conta com juros de 5% (compostos por trimestre) após um ano.
 ). Isso entrega
). Isso entrega  como resultado em. A equação agora é:
como resultado em. A equação agora é:  . Multiplique esses dois números e você terá
. Multiplique esses dois números e você terá  . Este é o valor da sua conta com juros de 5% (compostos por trimestre) após um ano.
. Este é o valor da sua conta com juros de 5% (compostos por trimestre) após um ano. , que você poderia esperar ao enviar a taxa de juros anual. Isso ilustra a importância de entender como e quando seus juros são compostos!
, que você poderia esperar ao enviar a taxa de juros anual. Isso ilustra a importância de entender como e quando seus juros são compostos! .
.Método 2 de 3: Calcular juros com contribuições periódicas

1. Primeiro use a fórmula de juros acumulados. Você também pode calcular juros em uma conta para a qual você transfere contribuições mensais regulares. Isso é útil se você economizar uma certa quantia todos os meses e colocar esse dinheiro em sua conta poupança. A equação completa fica assim: 

- Uma abordagem fácil é separar os juros compostos sobre o principal dos juros sobre as contribuições mensais (ou pagamentos/PMT). Para começar, primeiro calcule os juros sobre o capital ou principal usando a fórmula de poupança acumulada.
- Conforme descrito nesta fórmula, você pode calcular os juros em sua conta poupança com depósitos mensais recorrentes e juros compostos diários, mensais ou trimestrais.

2. Use a segunda parte da fórmula para calcular os juros dos seus depósitos. (PMT) representa o valor do seu depósito mensal.

3. Determine suas variáveis. Verifique sua conta ou contrato de investimento para encontrar as seguintes variáveis: capital `P`, taxa de juros anual `r` e número de parcelas por ano `n`. Se essas variáveis não estiverem prontamente disponíveis, entre em contato com seu banco para solicitar essas informações. A variável `t` representa o número de anos (ou partes dele) a serem calculados e `PMT` representa o pagamento/contribuição por mês. O valor `A` representa o valor total da conta após um período e depósitos de sua escolha.

4. Insira seus valores na fórmula. Usando o exemplo de P=1000, r=0,05 (5%), n=12 (compilado mensalmente), t=3 anos e PMT=100, obtemos a seguinte equação: 


5. Simplifique a equação. Comece a simplificar o objetivo  sempre que possível, dividindo a taxa de juros, 0,05, por 12. Isso é simplificado
sempre que possível, dividindo a taxa de juros, 0,05, por 12. Isso é simplificado  Você também pode simplificar adicionando um à taxa de juros dentro dos colchetes. A equação agora fica assim:
Você também pode simplificar adicionando um à taxa de juros dentro dos colchetes. A equação agora fica assim: 
 sempre que possível, dividindo a taxa de juros, 0,05, por 12. Isso é simplificado
sempre que possível, dividindo a taxa de juros, 0,05, por 12. Isso é simplificado  Você também pode simplificar adicionando um à taxa de juros dentro dos colchetes. A equação agora fica assim:
Você também pode simplificar adicionando um à taxa de juros dentro dos colchetes. A equação agora fica assim: 

6. Resolva os expoentes. Primeiro resolva os termos dentro dos expoentes,  , portanto
, portanto  . Em seguida, resolva os expoentes para simplificar a equação para
. Em seguida, resolva os expoentes para simplificar a equação para  Simplifique subtraindo um e você obtém
Simplifique subtraindo um e você obtém 
 , portanto
, portanto  . Em seguida, resolva os expoentes para simplificar a equação para
. Em seguida, resolva os expoentes para simplificar a equação para  Simplifique subtraindo um e você obtém
Simplifique subtraindo um e você obtém 

7. Faça os cálculos finais. Multiplique a primeira parte da equação e você terá $ 1.616. Resolva a segunda parte da equação dividindo primeiro o numerador pelo denominador da fração, e você terá  . Multiplique este número pelo valor do depósito (neste caso $ 100) para obter a segunda parte da equação. A equação agora é:
. Multiplique este número pelo valor do depósito (neste caso $ 100) para obter a segunda parte da equação. A equação agora é:  . O saldo da conta está agora nessas circunstâncias
. O saldo da conta está agora nessas circunstâncias  .
.
 . Multiplique este número pelo valor do depósito (neste caso $ 100) para obter a segunda parte da equação. A equação agora é:
. Multiplique este número pelo valor do depósito (neste caso $ 100) para obter a segunda parte da equação. A equação agora é:  . O saldo da conta está agora nessas circunstâncias
. O saldo da conta está agora nessas circunstâncias  .
.
8. Calcule os juros totais ganhos. Nesta equação, os juros reais são o valor total (A) menos o principal (P) e o número de pagamentos vezes o depósito (PMT*n*t). Assim no exemplo:  e depois disso
e depois disso  .
.
 e depois disso
e depois disso  .
.Método 3 de 3: Usando uma planilha para calcular juros compostos

1. Abra uma nova planilha. Excel e programas de planilhas semelhantes (por exemplo, Planilhas Google) podem economizar tempo fazendo esses cálculos para você e até fornecer atalhos na forma de funções financeiras integradas para ajudar a calcular juros compostos.

2. Nomeie suas variáveis. Ao usar uma planilha, é sempre útil ser o mais organizado e claro possível. Comece nomeando uma coluna de células com as informações importantes que você usará em seu cálculo (por exemplo,. juros, principal, tempo, n, depósitos).

3. Insira suas variáveis. Agora insira as informações que você tem sobre sua conta específica na próxima coluna. Isso não apenas torna a planilha mais fácil de ler e interpretar posteriormente, mas também deixa espaço para você alterar uma ou mais variáveis posteriormente, para analisar diferentes cenários de economia possíveis.

4. Monte sua equação. O próximo passo é inserir sua própria versão da equação de juros acumulados (  ), ou a versão estendida que leva em consideração seus depósitos mensais regulares (
), ou a versão estendida que leva em consideração seus depósitos mensais regulares (  ). Use qualquer célula vazia, comece com um `=` e use convenções matemáticas normais (colchetes quando necessário) para inserir a equação correta. Em vez de inserir variáveis como (P) e (n), digite os nomes correspondentes da célula onde você armazenou os valores dos dados, ou então apenas clique na célula desejada enquanto edita sua equação.
). Use qualquer célula vazia, comece com um `=` e use convenções matemáticas normais (colchetes quando necessário) para inserir a equação correta. Em vez de inserir variáveis como (P) e (n), digite os nomes correspondentes da célula onde você armazenou os valores dos dados, ou então apenas clique na célula desejada enquanto edita sua equação.
 ), ou a versão estendida que leva em consideração seus depósitos mensais regulares (
), ou a versão estendida que leva em consideração seus depósitos mensais regulares (  ). Use qualquer célula vazia, comece com um `=` e use convenções matemáticas normais (colchetes quando necessário) para inserir a equação correta. Em vez de inserir variáveis como (P) e (n), digite os nomes correspondentes da célula onde você armazenou os valores dos dados, ou então apenas clique na célula desejada enquanto edita sua equação.
). Use qualquer célula vazia, comece com um `=` e use convenções matemáticas normais (colchetes quando necessário) para inserir a equação correta. Em vez de inserir variáveis como (P) e (n), digite os nomes correspondentes da célula onde você armazenou os valores dos dados, ou então apenas clique na célula desejada enquanto edita sua equação.
5. Use funções financeiras. O Excel também oferece certas funções financeiras que podem ajudá-lo com seu cálculo. Especialmente `valor futuro` (TW) pode ser usado porque calcula o valor de uma conta em algum momento no futuro, dadas as mesmas variáveis às quais você se acostumou até agora. Para acessar esta função vá para uma célula vazia e digite `=TW(`. O Excel exibirá uma caixa de ajuda assim que você abrir o colchete de função para ajudá-lo a inserir os parâmetros corretos para a função.

 (a taxa de juros anual dividida por `n`). Isso calculará automaticamente os termos entre parênteses da função TW.
(a taxa de juros anual dividida por `n`). Isso calculará automaticamente os termos entre parênteses da função TW. o número total de parcelas sobre as quais o acúmulo é calculado e o número total de pagamentos. Em outras palavras, se o seu PMT não for 0, a função VA assumirá que você adiciona o valor do PMT em cada período, conforme definido pelo `número de parcelas`.
o número total de parcelas sobre as quais o acúmulo é calculado e o número total de pagamentos. Em outras palavras, se o seu PMT não for 0, a função VA assumirá que você adiciona o valor do PMT em cada período, conforme definido pelo `número de parcelas`. . Isso indica uma taxa de juros anual de 5% composta mensalmente por 12 meses, período em que você deposita $ 100/mês com um saldo inicial (principal) de $ 5.000. A resposta a esta função lhe dará o saldo da conta após 1 ano (€ 6.483,70).
. Isso indica uma taxa de juros anual de 5% composta mensalmente por 12 meses, período em que você deposita $ 100/mês com um saldo inicial (principal) de $ 5.000. A resposta a esta função lhe dará o saldo da conta após 1 ano (€ 6.483,70).Pontas
- Também é possível, embora mais complicado, calcular juros compostos em uma conta com pagamentos irregulares. Nesse método, o acúmulo de juros de cada pagamento/contribuição é calculado separadamente (utilizando a mesma equação descrita acima) e é melhor alcançado com uma planilha para facilitar o cálculo.
- Você também pode usar uma calculadora de juros anual online gratuita para determinar os juros da sua conta poupança. Pesquise na Internet por "calculadora de juros anual" ou "calculadora de juros percentual anual" para obter uma lista de sites que oferecem esse serviço gratuitamente.
Artigos sobre o tópico "Calcular juros em uma conta poupança"
Оцените, пожалуйста статью
Similar
Popular