Calculando juros

Contente

Degraus

A maioria das pessoas conhece o conceito de juros, mas nem todos sabem como calculá-lo. Juros é o valor agregado a um empréstimo ou adiantamento para pagar pelo uso do dinheiro de outras pessoas durante um período de tempo. Os juros podem ser calculados de três maneiras. Os juros ordinários são os mais fáceis de calcular e geralmente se aplicam a empréstimos de curto prazo. Juros compostos são um pouco mais complicados e valem mais. Afinal, a composição constante dos juros crescerá mais rápido e essa é a fórmula que a maioria dos bancos usa para empréstimos hipotecários. As informações necessárias para todos esses cálculos geralmente são as mesmas, mas a matemática é um pouco diferente para cada um.

Degraus

Método 1 de 3: Calculando Juros Simples

Imagem intitulada Calcular juros Etapa 1

1. Determine o valor principal. O principal é a quantia de dinheiro que você usará para calcular os juros. Pode ser um valor que você deposita em uma conta poupança ou coloca em algum tipo de investimento. Nesse caso, você pode calcular os juros que ganha. A alternativa é que, se você pedir dinheiro emprestado, como para uma hipoteca, o principal é o valor emprestado e você pode calcular os juros que deve.

Em ambos os casos, se você vai cobrar ou pagar juros, o valor do principal geralmente é simbolizado pela variável P.
Por exemplo, se você emprestou $ 2.000 de um amigo, esse $ 2.000 é o principal.

Imagem intitulada Calcular juros Etapa 2

2. Determinar o interesse. Antes de poder calcular quanto o principal aumentará em valor, você precisa saber a taxa de juros na qual o principal aumentará. Esse é o seu interesse. Os juros são geralmente anunciados ou acordados entre as partes antes que o empréstimo seja feito.

Por exemplo, suponha que você emprestou dinheiro a um amigo sob o acordo de que, após seis meses, ele devolverá os $ 2.000 com juros de 1,5%. O juro único é de 1,5%. Mas antes que você possa usar a porcentagem de 1,5%, você precisa convertê-la para um decimal. Para converter porcentagem em decimal, divida a porcentagem por 100:

1,5% 100=0,015.

Imagem intitulada Calcular juros Etapa 3

3. Confira o prazo do empréstimo. O termo é outro nome para a duração do empréstimo. Em alguns casos, você concorda com o prazo do empréstimo emprestando o valor. Por exemplo: a maioria das hipotecas tem prazo fixo. Em muitos casos, com um empréstimo privado, o mutuário e o credor concordam com um prazo pré-acordado.

É importante que a duração do prazo corresponda à taxa de juros, ou pelo menos seja medida nas mesmas unidades. Por exemplo: se se trata de uma taxa de juros anual, seu prazo também deve ser medido em anos. Se a taxa for anunciada como 3% ao ano, mas o empréstimo for apenas por seis meses, você estará calculando uma taxa de juros anual de 3% ao longo de um período de 0,5 ano.

Outro exemplo: se a taxa pactuada for de 1% ao mês, e você emprestar o dinheiro por seis meses, o prazo para o cálculo é de seis meses.

Imagem intitulada Calcular juros Etapa 4

4. Calcule os juros. Para calcular os juros, multiplique o principal pela taxa de juros e o prazo do empréstimo. Esta fórmula pode ser expressa algebricamente como:

eu = p * r * t

$I=P*r*t$

Usando o exemplo de empréstimo a um amigo acima, o principal (

p

$p$ ) igual a $ 2.000 e a porcentagem (

r

$r$ ) é 0,015 ao longo de um período de seis meses. Como o contrato neste exemplo foi por um período de seis meses, a variável

t

$t$ neste caso 1. Em seguida, calcule os juros da seguinte forma:

eu = p r t = (2000) (0, 015) (1) = 30

$I=Prt=(2000)(0,015)(1)=30$ . Assim, os juros devidos são de 30€.

Se você quiser calcular o valor total devido (A) com os juros e o produto do principal, use a fórmula

uma = p (1 + r t)

$A=P(1+rt)$ . Este cálculo fica assim:

uma = p (1 + r t)

$A=P(1+rt)$

uma = 2000 (1 + 0, 015 * 1)

$A=2000(1+0,015*1)$

uma = 2000 (1, 015)

$A=2000(1,015)$

uma = 2, 030

$A = 2.030$

Imagem intitulada Calcular Juros Passo 5

5. Tente outro exemplo. Digamos que você deposite $ 5.000 em uma conta poupança com juros anuais de 3%. Depois de apenas três meses, você saca o dinheiro, junto com os juros.

uma = p (1 + r t)

$A=P(1+rt)$

uma = 5000 (1 + 0, 03 * 0, 25)

$A=5000(1+0,03*0,25)$

uma = 5000 (1, 0075)

$A=5000(1,0075)$

uma = 5037, 5

$A=5037,5$

Em três meses você ganharia € 37,50 de juros.

Observe que t=0,25, pois três meses é um quarto (0,25) do período original de um ano.

Método 2 de 3: Calcular Juros Compostos

Imagem intitulada Calcular juros Etapa 6

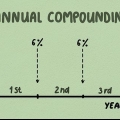
1. Entenda o que são juros compostos. Juros compostos significa que, à medida que você ganha juros, os juros são adicionados ao valor em sua conta e você começa a ganhar (ou pagar) juros sobre os juros. Um exemplo simples: se você depositar $ 100 com juros de 5% ao ano, terá ganho $ 5 de juros no final de um ano. Se você colocar isso de volta em sua conta, até o final do segundo ano você terá ganho 5% de $ 105, não apenas os $ 100 originais. Com o tempo, isso pode aumentar muito significativamente.

A fórmula para calcular o valor (A) dos juros compostos é assim:

$uma = p (1 + \frac{r}{n})^{n t}$ $A=P(1+{frac{r}{n}})^{{nt}}$

Imagem intitulada Calcular Juros Passo 7

2. Saiba o que significa o principal. Assim como os juros simples, o cálculo começa com o valor do principal. O cálculo é o mesmo se você vai calcular juros sobre dinheiro emprestado ou emprestado. O principal é geralmente denotado pela variável

p

$p$ .

Imagem intitulada Calcular Juros Passo 8

3. Determine a porcentagem. A taxa de juros deve ser acordada antes do empréstimo ser emprestado e exibida como um número decimal para o cálculo. Saiba que a porcentagem pode ser convertida em decimal dividindo-a por 100 (ou mais rápido, movendo o decimal duas posições para a esquerda). Certifique-se de saber para qual período a taxa de juros se aplica. A porcentagem tem

r

$r$ como um símbolo.

Por exemplo, uma empresa de cartão de crédito pode apresentar juros de 15% ao ano. No entanto, os juros geralmente são calculados mensalmente, então você provavelmente quer saber qual é a taxa de juros mensal. Nesse caso, você divide por 12 e recebe juros mensais de 1,25%. Esses dois percentuais, 15% ao ano e 1,25% ao mês, são iguais entre si.

Imagem intitulada Calcular Juros Passo 9

4. Saiba quando os juros são compostos. Juros compostos significam que os juros são calculados periodicamente e adicionados de volta ao valor principal. Para alguns empréstimos, isso pode acontecer uma vez por ano. Para outros, é todo mês ou todo trimestre. Você precisa saber com que frequência os juros serão compostos por ano.

Se os juros são compostos anualmente, então n=1.

Se os juros são compostos trimestralmente, então dinheiro n=4.

Imagem intitulada Calcular Juros Passo 10

5. Conheça o prazo do empréstimo. O prazo é o período sobre o qual os juros serão calculados. A duração é geralmente indicada em anos. Se você tiver que calcular os juros em um período diferente, precisará convertê-los em anos.

Por exemplo: com um empréstimo de um ano,

t = 1

$t=1$ . No entanto, com um prazo de 18 meses,

t = 1, 5

$t=1,5$ .

Imagem intitulada Calcular Juros Passo 11

6. Determine as variáveis da situação. Neste exemplo, suponha que você deposite $ 5.000 em uma conta poupança com 5%, juros compostos mensais. Qual é o valor dessa conta após três anos?

Primeiro determine quais variáveis você precisa para resolver o problema. Nesse caso:

p = 5000

$P=5000$

r = 0, 05

$r=0,05$

n = 12

$n=12$

t = 3

$t=3$

Imagem intitulada Calcular Juros Passo 12

7. Aplique a fórmula e calcule os juros compostos. Depois de entender o que precisa ser feito e quais variáveis são necessárias, aplique-as à fórmula para calcular a taxa de juros.

No problema acima fica assim:

uma = p (1 + \frac{r}{n})^{n t}

$A=P(1+{frac{r}{n}})^{{nt}}$

uma = 5000 (1 + 0, 05 12)^{12 * 3}

$A=5000(1+{frac{0,05}{12}})^{{12*3}}$

uma = 5000 (1 + 0, 00417) 36

$A=5000(1+0,00417)^{{36}}$

uma = 5000 (1, 00417) 36

$A=5000(1,00417)^{{36}}$

uma = 5000 (1, 1616)

$A=5000(1,1616)$

uma = 5808

$A=5808$

Então, após três anos de juros compostos, você tem um valor de € 808, além dos € 5.000 originalmente depositados.

Método 3 de 3: Calcular Juros Compostos Recorrentes

Imagem intitulada Calcular Juros Passo 13

1. Entenda o que são juros compostos rotativos. Como você viu no exemplo anterior, os juros compostos crescem mais rápido do que os juros simples, adicionando juros ao principal em determinados momentos. Compilar trimestralmente é mais valioso do que anualmente. Compilar mensalmente é ainda mais valioso do que anualmente. A situação mais lucrativa seria quando os juros são compostos constantemente - ou seja, a cada momento. Assim que os juros podem ser calculados, eles são adicionados à conta e adicionados ao principal. Este é, obviamente, apenas um caso teórico.

Usando um pouco de matemática, os matemáticos desenvolveram uma fórmula para simular juros que são continuamente compostos e adicionados à conta. Esta fórmula, usada para calcular os juros compostos rotativos, é:

$uma = p e r t$ $A=Pe^{{rt}}$

Imagem intitulada Calcular Juros Passo 14

2. Conheça as Variáveis para Cálculo de Juros. A fórmula de juros compostos rotativos é muito semelhante às situações anteriores, mas com alguns pequenos ajustes. As variáveis da fórmula são:

uma

$uma$ é o valor futuro (ou quantidade) de dinheiro que o empréstimo valerá após a composição dos juros.

p

$p$ é o principal.

A constante

e

$e$ . Embora pareça uma variável, na verdade é uma constante. A carta

e

$e$ é um número especial chamado "constante de Euler", em homenagem ao matemático Leonard Euler que descobriu suas propriedades.

As calculadoras gráficas mais avançadas têm um botão para

e X

$e^{x}$ . Se você pressionar este botão, com o número 1, assim

e 1

$e^{1}$ , então você vê que o valor de

e

$e$ é aproximadamente 2.718.

r

$r$ é o juro por ano.

t

$t$ é o prazo do empréstimo, em anos.

Imagem intitulada Calcular Juros Passo 15

3. Conheça os detalhes do seu empréstimo. Os bancos geralmente usam juros compostos rotativos para hipotecas. Suponha que você tenha € 200.000 querem tomar emprestado a juros de 4,2% para uma hipoteca de 30 anos. Portanto, as variáveis que você usará para esse cálculo são:

p = 200.000

$P = 200.000$

e

$e$ , novamente, não uma variável, mas a constante 2,718.

r = 0, 042

$r=0,042$

t = 30

$t=30$

Imagem intitulada Calcular Juros Passo 16

4. Use a fórmula para calcular os juros. Aplique os valores na fórmula para calcular o valor dos juros que você terá que pagar no empréstimo de 30 anos.