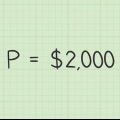Como Calcular Juros Compostos: 15 Passos (com Imagens)

Contente

Degraus
Pontas

Os juros compostos diferem dos juros simples, pois o rendimento dos juros é calculado sobre o investimento original (principal) e os juros acumulados até a data, em vez de apenas o principal. É por isso que as contas de juros compostos crescem mais rápido do que as contas de juros simples. Além disso, o valor crescerá ainda mais rápido se os juros forem compostos várias vezes ao ano. Os juros compostos (também chamados de juros) podem ser encontrados com vários produtos de investimento e também como juros de certos tipos de empréstimos, como dívidas de cartão de crédito. Com as equações certas, calcular quanto um valor vai crescer por meio de juros compostos é muito simples.

Degraus

Parte 1 de 3: Calculando os juros compostos anuais

Imagem intitulada Calcular Juros Compostos Etapa 1

1. Defina juros compostos anuais. A taxa de juros indicada no seu prospecto de investimento ou contrato de empréstimo é anual. Se você fizer um empréstimo de carro com, por exemplo, 6% de juros, pagará 6% de juros ao ano. Os juros compostos de final de ano são o cálculo de juros compostos mais fácil.

Os juros compostos de uma dívida podem ser calculados anualmente, mensalmente ou até diariamente.
Quanto mais vezes sua dívida for composta, mais rápido seus juros acumularão.
Você pode analisar os juros compostos do ponto de vista de um investidor ou devedor. Os juros compostos calculados com frequência significam que a receita dos juros do investidor crescerá a uma taxa mais rápida. Isso também significa que o devedor deve mais juros sobre uma dívida pendente.
Por exemplo, os juros podem ser calculados anualmente em uma conta poupança, enquanto os juros de um empréstimo rápido podem ser calculados mensalmente ou até semanalmente.

Imagem intitulada Calcular Juros Compostos Etapa 2

2. Calcular os juros anuais compostos para o ano 1. Suponha que você possua um título do governo de € 1 .000, a uma taxa de juros de 6%. Os títulos do governo pagam dividendos a cada ano com base em juros e valor presente.

Os juros para o ano 1 serão então de € 60 (€ 1.000 x 6%).

Para calcular os juros para o ano 2, você precisa adicionar o principal original ao total de juros até a data. Neste caso, o capital do ano 2 é igual a 1€.060 (€ 1.000 + € 60). O valor da obrigação é, portanto, € 1.060 e os juros a serem pagos são calculados com base nesse valor.

Imagem intitulada Calcular Juros Compostos Passo 3

3. Calcular os juros compostos para anos posteriores. Para ver o maior impacto dos juros compostos, calcule os juros para anos posteriores. O principal continua a crescer de ano para ano.

Multiplique o principal do ano 2 pela taxa de juros do título ($ 1.060 X 6% = € 63,60). O juro obtido é superior 3,60€ (63,60€ - 60,00€). Isso porque o principal aumentou de $ 1.000 a 1€.060.

Para o ano 3, o principal é de € 1.123,60 (€ 1.060 + € 63,60). Os juros para o ano 3 são de € 67,42. Esse valor é adicionado ao principal para o cálculo do ano 4.

Quanto mais tempo uma dívida estiver em aberto, maior será o impacto dos juros compostos. Pendente significa que a dívida ainda deve ser paga pelo devedor.

Sem juros compostos, os juros ganhos no ano 2 seriam $ 60 (€ 1.000 X 6%). Na verdade, a cada ano os juros seriam de $ 60 se você tivesse juros compostos. Isso é conhecido como juros simples.

Imagem intitulada Calcular Juros Compostos Etapa 4

4. Criar um documento do Excel para calcular juros compostos. Pode ser útil visualizar juros compostos criando um modelo simples em Excel do crescimento do seu investimento. Comece abrindo um documento e rotule a célula superior na coluna A, B e C como "Ano", "Valor" e "Juros ganhos", respectivamente.

Digite os anos (0-5) nas células A2 a A7.

Digite o principal na célula B2. Suponha que você começou com € 1.000. Tipo 1000.

Na célula B3, digite `= B2 *1,06` e pressione enter. Isso significa que seus juros são compostos anualmente com juros de 6% (0,06). Clique no canto inferior direito da célula B3 e arraste a fórmula para a célula B7. Os números agora estão preenchidos corretamente.

Coloque um 0 na célula C2. Na célula C3 digite `=B3-B2` e pressione Enter. Isso dá a diferença entre os valores nas células B3 e B2, que representa o interesse. Clique no canto inferior direito da célula C3 e arraste a fórmula para a célula C7. Os valores devem ser preenchidos automaticamente.

Repita este procedimento por quantos anos você quiser acompanhar. Você também pode alterar facilmente os valores do principal e da taxa de juros alterando as fórmulas usadas e o conteúdo das células.

Parte 2 de 3: Calculando os juros compostos sobre investimentos

Imagem intitulada Calcular Juros Compostos Etapa 5

1. Aprenda a fórmula dos juros compostos. A fórmula de juros compostos calcula o valor futuro do investimento após um certo número de anos. A fórmula em si é a seguinte:

f V = p (1 + \frac{eu}{c})^{n * c}

$FV=P(1+{frac{i}{c}})^{{n*c}}$ As variáveis dentro da equação são definidas da seguinte forma:

`FV` é o valor futuro. Este é o resultado do cálculo.
`P` é o seu principal.
`i` é a taxa de juros anual.
`c` é a taxa de juros compostos (com que frequência os juros compostos são calculados anualmente).
`n` é o número de anos para calcular.

Imagem intitulada Calcular Juros Compostos Etapa 6

2. Colete as variáveis para a fórmula de juros compostos. Se os juros forem calculados com mais frequência do que anualmente, é difícil calcular a fórmula manualmente. Você pode usar uma fórmula de juros compostos para qualquer cálculo. Para usar a fórmula, você precisa das seguintes informações:

Determine o valor principal do investimento. Este é o valor original do seu investimento. Isso pode ser quanto você depositou em sua conta ou o preço original do título. Por exemplo, suponha que seu principal em uma conta de investimento seja de € 5.000 é.

Encontre a taxa de juros do investimento. A taxa de juros deve ser um valor anual, expresso como uma porcentagem do valor principal. Por exemplo, uma taxa de juros de 3,45% sobre o principal de € 5.000.

Ao calcular, a taxa de juros deve ser inserida como um decimal. Converta dividindo a taxa de juros por 100. Neste exemplo torna-se 3,45/100 = 0,0345.

Você também precisa saber com que frequência os juros são compostos. Os juros geralmente são compostos anualmente, mensalmente ou diariamente. Suponha, por exemplo, que se trata de juros mensais. Isso significa que sua taxa de juros (`c`) deve ser inserida como 12.

Determine em qual período você deseja calcular. Pode ser uma meta anual de crescimento, como 5 ou 10 anos, ou o vencimento do título. A data de vencimento de uma obrigação é a data em que o capital do investimento deve ser reembolsado. Como exemplo, estamos usando dois anos aqui, então insira 2.

Imagem intitulada Calcular Juros Compostos Passo 7

3. Use a fórmula. Substitua suas variáveis nos lugares certos. Por favor, verifique se você os digitou corretamente. Em particular, certifique-se de que os juros sejam inseridos na forma decimal e que você tenha usado o valor correto para `c` (taxa de juros).

O exemplo de investimento é então inserido da seguinte forma:

f V = 5000 (1 + 0, 0345 12)^{2 * 12}

$FV=5000(1+{frac{0,0345}{12}})^{{2*12}}$

Calcule o expoente e a parte da fórmula entre parênteses separadamente. Este é um conceito da matemática chamado `ordem das operações`. Você pode ler artigos sobre a ordem das operações no wikiHow.

Imagem intitulada Calcular a Etapa de Juros Compostos 8

4. Complete os cálculos matemáticos na fórmula. Simplifique o problema resolvendo primeiro os termos entre parênteses, começando com a fração.

Primeiro calcule a fração entre parênteses. O resultado:

f V = 5000 (1 + 0, 00288) 2 * 12

$VF=5000(1+0,00288)^{{2*12}}$

Adicionar números entre parênteses juntos. O resultado:

f V = 5000 (1, 00288) 2 * 12

$VF=5000(1,00288)^{{2*12}}$

Resolva a multiplicação dentro do expoente (a última parte acima do parêntese de fechamento). O resultado deve ficar assim:

f V = 5000 (1, 00288) 24

$VF=5000(1,00288)^{{24}}$

Eleve o número entre parênteses à potência do expoente. Isso pode ser feito em uma calculadora inserindo primeiro o valor entre parênteses (1,00288 no exemplo), pressionando o botão

X y

$x^{y}$ , e, em seguida, inserindo o expoente (24 neste caso), após o qual você pressiona Enter. O resultado deste exemplo é

f V = 5000 (1, 0715)

$VF=5000(1,0715)$ .

Por fim, multiplique o principal pelo número entre parênteses. O resultado no exemplo é €5.000 x 1,0715 = € 5.357,50. Este é o saldo da conta no final do segundo ano.

Imagem intitulada Calcular Juros Compostos Passo 9

5. Subtraia o principal da sua resposta. Isso retorna o valor dos juros.

Subtrair o principal de € 5.000 do valor futuro de 5€.357,50 e ganha 5€.375,50 - € 5.000 = € 357,50

Você ganhou € 357,50 de juros após dois anos.

Parte 3 de 3: Calculando os juros compostos com pagamentos regulares

Imagem intitulada Calcular Juros Compostos Passo 10

1. Aprenda a fórmula. Os cálculos de juros compostos podem crescer ainda mais rápido se você fizer depósitos regulares, como transferir um valor mensal para uma conta poupança. A fórmula é mais longa do que a usada para calcular juros compostos sem pagamentos regulares, mas segue os mesmos princípios. A fórmula é a seguinte:

f V = p (1 + \frac{eu}{c})^{n * c} + R ((1 + \frac{eu}{c})^{n * c} - 1) \frac{eu}{c}

$FV=P(1+{frac{i}{c}})^{{n*c}}+{frac{R((1+{frac{i}{c}})^{{n *c}}-1)}{{frac{i}{c}}}}$ As variáveis na equação também são as mesmas da equação anterior, com uma adição:

`P` é o principal.
`i` é a taxa de juros anual.
`c` é a frequência da taxa de juros e representa o número de vezes que os juros são compostos anualmente.
`n` é o número de anos.
`R` é o valor da contribuição mensal.

Imagem intitulada Calcular a Etapa de Juros Compostos 11

2. Preencha as variáveis. Para calcular o valor futuro desse tipo de conta, você precisa do principal (ou valor presente) da conta, a taxa de juros anual, a frequência dos juros, o número de anos que está sendo calculado e o valor da sua contribuição mensal. Esta informação deve estar no seu contrato de investimento.

Certifique-se de converter a taxa de juros anual para um número decimal. Você faz isso dividindo a porcentagem por 100. Por exemplo, assumindo a taxa de juros acima de 3,45%, dividimos 3,45 por 100 e você obtém 0,0345.

Para a frequência de juros, você usa o número de vezes por ano que os juros são calculados. Isso significa número 1 anual, 12 mensal e 365 diário (não se preocupe com anos bissextos).

Imagem intitulada Calcular a Etapa de Juros Compostos 12

3. Preencha as variáveis. Continuamos com o exemplo acima: suponha que você decida transferir € 100 por mês para sua conta. Sobre esta conta, com capital de 5€.000, os juros compostos são calculados mensalmente com uma taxa de juros anual de 3,45%. Vamos calcular o crescimento da conta em dois anos.

A fórmula final usando essas informações é a seguinte:

f V = 5000 (1 + 0, 0345 12)^{2 * 12} + 100 ((1 + 0, 0345 12)^{2 * 12} - 1) \frac{0, 0345}{12}

$FV=5000(1+{frac{0.0345}{12}})^{{2*12}}+{frac{100((1+{frac{0.0345}{12}}) ^{{2 *12}}-1)}{{frac{0.0345}{12}}}}$

Imagem intitulada Calcular Juros Compostos Passo 13

4. Resolva a equação. Novamente, não se esqueça da ordem correta das operações. Isso significa que você começa calculando os valores dentro dos parênteses.

Primeiro resolva as frações dentro dos parênteses. Isso significa dividir `i` por `c` em três lugares, tudo para o mesmo resultado de 0,00288. Agora a equação fica assim:

f V = 5000 (1 + 0, 00288) 2 * 12 + 100 ((1 + 0, 00288) 2 * 12 - 1) 0, 00288

$VF=5000(1+0,00288)^{{2*12}}+{frac{100((1+0,00288)^{{2*12}}-1)}{0,00288}}$

Resolva a adição entre parênteses. Isso significa que você adiciona o 1 ao resultado da parte anterior. Por isso:

f V = 5000 (1, 00288) 2 * 12 + 100 ((1, 00288) 2 * 12 - 1) 0, 00288

$VF=5000(1,00288)^{{2*12}}+{frac{100((1,00288)^{{2*12}}-1)}{0,00288}}$

Resolva a multiplicação dentro dos expoentes. Isso significa multiplicar os dois números menores e acima dos parênteses de fechamento. No exemplo: 2 x 12 = 24. Por isso:

f V = 5000 (1, 00288) 24 + 100 ((1, 00288) 24 - 1) 0, 00288

$VF=5000(1,00288)^{{24}}+{frac{100((1,00288)^{{24}}-1)}{0,00288}}$

Resolva os expoentes. Isso significa aumentar o valor entre parênteses com o resultado da última etapa. Em uma calculadora, isso é feito inserindo o valor entre parênteses (1,00288 no exemplo), pressione

X y

$x^{y}$ e insira o valor do expoente (24). Por isso:

f V = 5000 (1, 0715) + 100 (1, 0715 - 1) 0, 00288

$VF=5000(1,0715)+{frac{100(1,0715-1)}{0,00288}}$

subtrair. Subtraia 1 do resultado da última etapa na parte direita da equação (1,0715 - 1). Por isso:

f V = 5000 (1, 0715) + 100 (0, 0715) 0, 00288

$VF=5000(1,0715)+{frac{100(0,0715)}{0,00288}}$

Multiplicar. Isso significa multiplicar o principal pelo valor dentro do primeiro conjunto de parênteses e a contribuição mensal pelo mesmo valor entre parênteses. Por isso:

f V = 5357, 50 + 7, 15 0, 00288

$FV=5357,50+{frac{7,15}{0,00288}}$

Divida a fração. Por isso:

f V = 5357, 50 + 2482, 64

$VF=5357,50+2482,64$

Adicionar. Por fim, some os dois números para obter o valor futuro da conta. Então: 5€.357,50 + € 2.482,64 = € 7.840,14. Este é o valor da conta após os dois anos.

Imagem intitulada Calcular a Etapa de Juros Compostos 14

5. Subtraia o principal e os pagamentos. Para calcular os juros ganhos, você precisa subtrair o valor que você depositou. Isso significa somar o principal, € 5.000, ao valor total dos valores depositados, ou seja: 24 contribuições (2 anos x 12 meses/ano) vezes os 100€ que depositou em cada mês, num total de 2400€. O total é de 5€.000 + € 2.400 = € 7.400. Sorteio de € 7.400 de desconto no valor futuro de 7€.840,14, e você tem o valor dos juros, € 440,14.

Imagem intitulada Calcular a Etapa de Juros Compostos 15

6. Expanda seu cálculo. Para realmente ver o benefício dos juros compostos, imagine que você continua depositando dinheiro na mesma conta todos os meses por 20 anos (em vez de dois). Neste caso, o valor futuro torna-se cerca de 45.000 dólares, embora você gaste apenas € 29.000, o que significa que seus juros acumulados são de € 16.000 equivale a.

Pontas

Você também pode calcular facilmente os juros compostos usando uma calculadora de juros online. Você pode encontrar um exemplo no site do governo dos EUA: https://www.investidor.gov/tools/calculators/compound-interest-calculator.
Uma maneira rápida de determinar juros compostos é a `regra 72`. Comece dividindo 72 pela quantidade de juros que você recebe, digamos 4%. Então neste caso 72/4 = 18. Esse resultado, 18, é aproximadamente o número de anos que levará para dobrar seu investimento à taxa de juros atual. Tenha em mente que a regra 72 é apenas uma aproximação rápida, não um resultado exato.
Você também pode usar esses cálculos para fazer cálculos "e se" que podem dizer quanto você ganhará dependendo da taxa de juros, principal, taxa de juros ou número de anos.