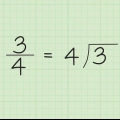Converter um Decimal Repetitivo em uma Fração: 9 Passos (com Imagens)

Contente

Degraus
- Parte 1 de 2: Convertendo decimais simples periódicos
- Parte 2 de 2: Convertendo números com decimais repetidos e não periódicos

Uma dízima periódica, também chamada de dízima periódica, é um número decimal que contém um dígito ou grupo de dígitos que se repete indefinidamente em intervalos regulares. Decimais repetidos podem ser complicados de trabalhar, mas eles também podem ser convertidos em uma fração. Às vezes, os decimais repetidos são indicados por uma linha acima dos dígitos repetidos. O número 3,7777 com 7 como dígito repetido, por exemplo, também pode ser escrito como 3.7. Para converter um número como este em uma fração, escreva-o como uma equação, multiplique e subtraia para remover a dízima periódica e resolva a equação.

Degraus

Parte 1 de 2: Convertendo decimais simples periódicos

Imagem intitulada Converter decimais repetidos em frações Etapa 1

1. Encontre a dízima periódica. Por exemplo: o número 0,4444 tem uma dízima periódica 4. É uma dízima periódica padrão no sentido de que não há parte não periódica no número decimal. Conte quantas casas decimais repetidas (repetidas) existem no padrão.

Quando sua equação estiver escrita, multiplique-a por 10^y`, através do qualy é igual ao número de dígitos repetidos no padrão.
No exemplo de 0,4444, há um dígito que se repete, então você multiplica a equação por 10^1.
Para uma dízima periódica de 0,4545, existem dois números que se repetem e você multiplicaria sua equação por 10^2.
Para três números repetidos, multiplique por 10^3, etc.

Imagem intitulada Converter decimais repetidos em frações Etapa 2

2. Reescreva o decimal como uma equação. Escreva de modo que x seja igual ao número original.Neste caso, a equação é x = 0.4444. Como há apenas um dígito na dízima periódica, multiplique a equação por 10^1 (que é igual a 10).

No exemplo: onde x = 0,4444, então 10x = 4,4444.

No exemplo x = 0,4545 há dois números repetidos, então você multiplica ambos os lados da equação por 10^2 (que é igual a 100), dando-lhe 100x = 45.4545 fica.

Imagem intitulada Converter decimais repetidos em frações Etapa 3

3. Remova a dízima periódica. Você faz isso subtraindo x de 10x. Lembre-se que o que você faz de um lado da equação, você tem que fazer do outro lado, então:

10x – 1x = 4,4444 – 0,4444

À esquerda você tem 10x - 1x = 9x. No lado direito você tem 4,4444 – 0,4444 = 4

Portanto: 9x = 4

Imagem intitulada Converter decimais repetidos em frações Etapa 4

4. Resolva para x. Depois de saber o que 9x é igual, você pode determinar o que x é igual dividindo ambos os lados da equação por 9:

No lado esquerdo da equação você tem 9x ÷ 9 = x. No lado direito da equação você tem 09/04

É por isso que x = 4/9, e pode ser a dízima periódica 0,4444 ser escrito como a fração 09/04.

Imagem intitulada Converter decimais repetidos em frações Etapa 5

5. Reduza a fração. Converta a fração para sua forma mais simples (se houver) dividindo o numerador e o denominador pelo maior fator comum.

No exemplo de 4/9 essa é a forma mais simples.

Parte 2 de 2: Convertendo números com decimais repetidos e não periódicos

Imagem intitulada Converter decimais repetidos em frações Etapa 6

1. Determine os números repetidos. Não é incomum que um número tenha dígitos não repetidos antes da dízima periódica, mas eles ainda podem ser convertidos em frações.

Tomemos por exemplo o número 6.215151. Aqui está 6.2 não repetitivos, e os números repetidos são 15.
Observe novamente quantos dígitos repetidos estão no padrão, porque você vai multiplicar por 10^y com base nesse número.
Neste exemplo, há dois números repetidos, então multiplique a equação por 10^2.

Imagem intitulada Converter decimais repetidos em frações Etapa 7

2. Escreva o problema como uma equação e subtraia as dízimas periódicas. Novamente, se x = 6,215151, então 100x = 621,5151. Para remover as dízimas periódicas, subtraia de ambos os lados da equação:

100x – x (= 99x) = 621.5151 – 6.215151 (= 615,3)

Assim, 99x = 615,3

Imagem intitulada Converter decimais repetidos em frações Etapa 8

3. Resolva para x. Como 99x = 615,3, divida ambos os lados da equação por 99. Isso lhe dá x = 615,3/99.

Imagem intitulada Converter decimais repetidos em frações Etapa 9

4. Remova o decimal no contador. Faça isso multiplicando o numerador e o denominador por 10^z`, através do qualz é igual ao número de decimais que você tem que mover para eliminar o decimal. Em 615.3 você tem que mover o decimal uma posição, o que significa que você multiplica o numerador e o denominador por 10^1:

615,3×10 / 99 x 10 = 6153/990

Simplifique a fração dividindo o numerador e o denominador pelo máximo divisor comum (neste caso 3), e você obtém x = 2,051 / 330