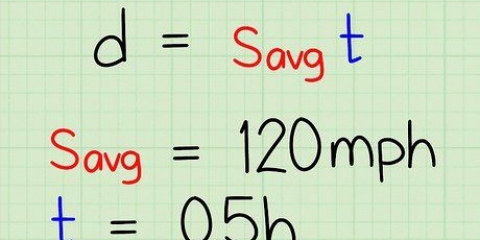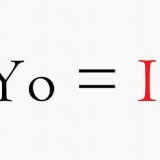Em nosso exemplo, digamos que seja exatamente duas horas custo para fazer esta viagem. 
No nosso exemplo, esta equação é 100 milhas/2 horas = 50 milhas/hora(cerca de 80 km/h). 
As unidades de velocidade são as unidades de distância sobre as unidades de tempo. Em nosso exemplo, nossas unidades são milhas/hora (ou milhas por hora) já que medimos a distância em milhas e o tempo em horas. 

Por exemplo, digamos que no problema de exemplo acima precisamos de nossa resposta em milhas em vez de quilômetros. Existem cerca de 1,6 quilômetros em uma milha, então podemos convertê-lo assim: Observe que, como os quilômetros estão na parte inferior da fração, eles podem ser riscados com os quilômetros na resposta original, deixando a resposta em milhas. Este site contém conversões para as unidades mais comuns. 
Por exemplo, digamos que um avião voe cinco vezes em um círculo com 20 milhas de largura. O avião completa esta viagem em meia hora. Neste exemplo, ainda precisamos determinar exatamente a distância que o avião percorreu antes de encontrarmos a velocidade. Podemos usar a equação para a distância ao redor de um círculo (sua circunferência) em vez de "uma" em nossa comparação. Esta equação é circunferência = 2πr onde r = o raio do círculo. Podemos resolver isso da seguinte forma: 
Para ilustrar essa diferença, imagine a última viagem que você fez em um carro. É altamente improvável que você tenha percorrido a mesma velocidade durante toda a viagem. Em vez disso, você começou devagar e gradualmente atingiu sua velocidade máxima e diminuiu em semáforos, engarrafamentos e assim por diante. Se você usar a equação de velocidade padrão para calcular sua velocidade para a viagem, essas mudanças de velocidade não serão refletidas. Em vez disso, você receberá uma resposta em algum lugar entre as diferentes velocidades em que viajou. 

Por esta razão, ambos os carros no problema do exemplo acima têm um velocidade (velocidade) por 50 km/h. 
Suponha que a posição de um objeto em metros seja dada pela equação 3t + t - 4 onde t = tempo em segundos. Queremos saber qual é a velocidade do objeto em t = 4 segundos. Neste caso, podemos resolver da seguinte forma: Agora preenchemos t = 4: 
Suponha que um objeto tenha uma aceleração constante (em m/s dada por a (t) = -30. Digamos também que o objeto tem uma velocidade inicial de 10 m/s. Precisamos encontrar a velocidade em t = 12s. Neste caso, podemos resolver da seguinte forma: Para encontrar C, resolvemos para v(t) para t = 0. Lembre-se que a velocidade inicial do objeto é 10 m/s. Agora podemos inserir t = 12 segundos.
Calcular velocidade
Contente
Velocidade é a medida de `quão rápido` algo está indo em um determinado momento. Se você já olhou para o velocímetro de um carro enquanto dirigia, viu como a velocidade é medida - quanto mais longe a agulha vai, mais rápida a velocidade do carro. Existem algumas maneiras diferentes de calcular a velocidade, dependendo de quais informações você possui. Para fins gerais, a equação é velocidade = distância/tempo (ou s = a/t) geralmente a maneira mais fácil de calcular a velocidade.
Degraus
Método 1 de 3: Usando a equação de velocidade padrão

1. Encontre a distância que um objeto percorreu. A equação básica que a maioria das pessoas usa para descobrir o quão rápido algo está acontecendo é muito fácil de usar. A primeira coisa que você precisa saber é quanta distância o objeto percorreu. Em outras palavras, a que distância está o ponto inicial do ponto final?
- Esta equação será mais fácil de entender com um exemplo. Digamos que façamos um passeio de carro até um parque temático de 100 milhas (cerca de 161 quilômetros). Nas próximas etapas, usaremos essas informações para resolver essa equação.

2. Encontre o tempo que o objeto levou para percorrer essa distância. A próxima informação que você precisa é quanto tempo levou o objeto para viajar. Em outras palavras, quanto tempo levou para ir do ponto inicial ao ponto final?

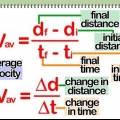
3. Divida a distância pelo tempo para encontrar a velocidade. Tudo o que você precisa são essas duas informações para determinar sua velocidade para a viagem. A distancia cerca de o tempo lhe dá a velocidade do objeto.

4. Não se esqueça das unidades. Rotule sua resposta com as unidades apropriadas (como milhas por hora, etc.).) é crítico. Sem unidades, pode ser difícil para outras pessoas entenderem o que sua resposta significa. Você também pode perder pontos se esquecer de anotar a unidade em uma tarefa escolar.
Método 2 de 3: Resolvendo outros problemas

1. Isole as diferentes variáveis para calcular distância e tempo. Depois de conhecer o básico da equação da velocidade, você pode usá-la para encontrar mais do que apenas velocidade. Por exemplo, se você conhece a velocidade e uma das outras variáveis, pode reorganizar a equação para encontrar a informação que está faltando.
- Suponha que sabemos que um trem viajou a uma velocidade de 20 quilômetros por hora durante quatro horas, mas precisamos saber a distância percorrida. Nesse caso, podemos reorganizar a equação e resolvê-la desta forma:
- velocidade = distância/tempo
- velocidade × tempo = (distância/tempo) × tempo
- velocidade × tempo = distância
- 20 km/h × 4 h = distância = 80 quilômetros

2. Converta suas unidades, se necessário. Às vezes você pode calcular a velocidade em uma unidade diferente da que você precisa. Neste caso você deve fatores de conversão use para colocar sua resposta na unidade correta. Para fazer isso, escreva as relações entre suas unidades como uma fração e multiplique. Quando você multiplica, você gira sua fração conforme necessário para se livrar das unidades que não deseja. Isso é muito mais fácil do que parece!
- 80 quilômetros × 1 milha/1.6 quilômetros = 50 milhas

3. Substitua a variável `distância` por fórmulas de distância, se necessário. Os objetos nem sempre viajam em linhas retas agradáveis e convenientes. Caso contrário, talvez você não consiga simplesmente inserir um valor numérico para a distância na equação de velocidade padrão. Em vez disso, você pode precisar substituir a em s = a/t por uma fórmula que modela a distância que o objeto percorreu.
- s = (2 × π × r)/t
- s = (2 × π × 10)/0.5
- s = 62.83/0.5 = 125.66 milhas/hora

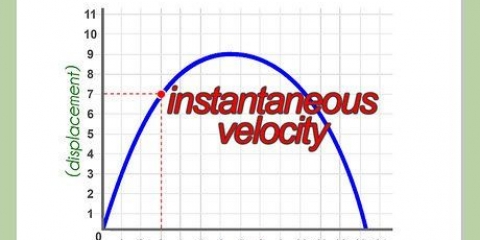
4. Veja que s = a/t a média velocidade dá. A equação simples e conveniente que usamos para encontrar a velocidade tem uma grande falha. O valor que dá é tecnicamente uma velocidade média. Isso significa que ele assume que o objeto que você está medindo tem a mesma velocidade durante todo o percurso. Como veremos abaixo, pode ser mais difícil encontrar a velocidade de um objeto a qualquer momento.
Método 3 de 3: Calculando a velocidade instantânea
Observação: Esta seção usa técnicas desconhecidas para aqueles que não estudaram cálculo. Consulte nossos artigos de cálculo para obter ajuda.

1. Observe que a velocidade é definida como a magnitude da velocidade. Cálculos de velocidade de nível mais alto podem ser confusos porque matemáticos e cientistas usam definições diferentes para "velocidade". Uma velocidade (velocidade) tem dois componentes: um magnitude e um direção. A magnitude é igual à velocidade do objeto. Uma mudança de direção causará uma mudança na velocidade (velocidade), mas não na velocidade.
- Por exemplo, digamos que dois carros estejam dirigindo em direções opostas. Os velocímetros de ambos os carros marcam 50 km/h, então ambos têm a mesma velocidade. No entanto, como eles se afastam, podemos dizer que um carro é um Velocidade da velocidade) de -50 km/h e um tem um Velocidade da velocidade) de 50km/h.
- Assim como você pode calcular a velocidade instantânea (velocidade), você também pode calcular a calcular a velocidade instantânea (velocidade).

2. Use valores absolutos para velocidades negativas. Os objetos podem ter velocidades de magnitude negativa (se estiverem se movendo em uma direção negativa em relação a outra coisa). No entanto, não existe uma velocidade negativa (velocidade), então nestes casos o valor absoluto de magnitude altera a velocidade do objeto.

3. Derivando uma função de posição. Se você tem uma função s(t) que lhe dá a posição de um objeto em relação ao tempo, então a derivada de s(t) lhe dará Velocidade da velocidade) dando em relação ao tempo. Basta inserir um valor de tempo nesta equação para a variável t (ou qualquer que seja o valor de tempo) para obter a velocidade neste ponto. A partir daqui, encontrar a velocidade é fácil.
- 3t + t - 4
- s`(t) = 2 × 3t + 1
- s`(t) = 6t + 1
- s`(t) = 6(4) + 1 = 24 + 1 = 25 metros/segundo. Esta é tecnicamente uma medida de velocidade (velocidade), mas como é positiva e a direção não é mencionada no problema, podemos essencialmente usá-la para velocidade.

4. Tome a integral de uma função de aceleração. Aceleração é uma forma de mudança na velocidade de um objeto ao longo do tempo medir. Este tópico é um pouco complexo demais para explicar completamente neste artigo. No entanto, é útil notar que quando você tem uma função a(t) que fornece aceleração em relação ao tempo, a integral de a(t) fornece velocidade (velocidade) em relação ao tempo. Observe que é útil conhecer a velocidade inicial do objeto para que você possa definir a constante resultante de uma integral indefinida.
- a(t) = -30
- v(t)= ∫ a(t)dt =∫ -30dt = -30t + C
- v(0) = 10 = -30(0) + C
- 10 = C, então v(t) = -30t + 10
- v(12) = -30(12) + 10 = -360 + 10 = -350. Como a velocidade é o valor absoluto da velocidade, a velocidade do objeto é 350 metros/segundo.
Pontas
- A prática leva à perfeição! Tente fazer suas próprias somas substituindo números diferentes nos problemas de exemplo acima.
- Se você estiver procurando uma maneira rápida de calcular para cálculos avançados de velocidade, use aqui do que a calculadora derivada online e a calculadora integral online aqui.
Artigos sobre o tópico "Calcular velocidade"
Оцените, пожалуйста статью
Popular