Observe, no entanto, que se as unidades de tempo usadas em seu valor de velocidade média forem diferentes daquelas em seu valor de tempo, você precisará converter uma ou outra para corresponder. Por exemplo, se uma velocidade média for medida em km/h e o tempo estiver em minutos, você teria que dividir o tempo por 60 para convertê-lo em horas. Vamos resolver nosso problema de exemplo. 120 km/h × 0,5 h = 60 km. Observe que as unidades de tempo (horas) cair contra as unidades no denominador da velocidade média (horas), deixando apenas as unidades de distância (km). 
Suponha que sabemos que um carro percorreu 60 km em 50 minutos, mas não temos valor para a velocidade média durante a condução. Neste caso podemos usar a variável sgema isolar na equação base para a distância, e obtemos sgema = d/t para obter. Então calculamos 60 km/50 minutos = 1,2 km/min. Observe que em nosso exemplo, nossa resposta para velocidade tem uma unidade incomum (km/minuto). Para obter sua resposta na forma mais comum de km/h, multiplique por 60 minutos/h e obtenha `72 km/h para obter. 
Exemplo: No exemplo do problema acima, concluímos que para percorrer 60 km em 50 minutos, teríamos que viajar a 72 km/h. No entanto, isso só é verdade se viajarmos a uma velocidade durante toda a viagem. Por exemplo, dirigindo metade da viagem a 80 km/h e a outra metade a 64 km/h, ainda percorremos 60 km em 50 minutos — 72 km/h = 60 km/50 min = ????? Soluções matemáticas o uso de derivadas geralmente é uma escolha melhor do que a fórmula da distância para definir a velocidade de um objeto em situações reais, porque as mudanças na velocidade são prováveis. 

Observe que esta fórmula utiliza valores absolutos (o símbolo |). Valores absolutos significam simplesmente que os termos dentro dos símbolos se tornam positivos quando são negativos. Por exemplo, digamos que paramos em um trecho de estrada perfeitamente reto ao longo do caminho. Se houver uma pequena cidade 5 km à nossa frente e uma cidade 1 km atrás de nós, qual a distância entre as duas cidades?? Se tomarmos a cidade 1 como x1 = considere 5 e cidade 2 como x2 = -1, então podemos encontrar d, a distância entre as duas cidades, como segue: d = |x2 - X1| = |-1 - 5| = |-6| = 6 km. 
A fórmula da distância no espaço bidimensional usa a teorema de Pitágoras, que afirma que a hipotenusa de um triângulo retângulo é igual à raiz quadrada dos outros dois lados. Por exemplo, digamos que temos dois pontos no plano x-y: (3, -10) e (11, 7) que representam respectivamente o centro de um círculo e um ponto no círculo. Para encontrar a distância reta entre esses dois pontos, podemos resolver o seguinte: d = √((x2 - X1) + (s2 - y1)) d = √((11 - 3) + (7 - -10)) d = √(64 + 289) d = √(353) = 18,79 
Exemplo: Digamos que como um astronauta pairando no espaço perto de dois asteróides. Um está cerca de 8 km à nossa frente, 2 km à nossa direita e 5 km abaixo de nós, enquanto o outro está a 3 km atrás de nós, 3 km à nossa esquerda e 4 km acima de nós. Se representarmos as posições desses asteróides com as coordenadas (8.2,-5) e (-3,-3.4), podemos encontrar a distância entre os dois da seguinte forma: d = √((-3 - 8) + (-3 - 2) + (4 - -5)) d = √((-11) + (-5) + (9)) d = √(121 + 25 + 81) d = √(227) =15,07 km
Calcular distância
Contente
Distância, muitas vezes referida como a variável d, é uma medida do espaço ocupado por uma linha reta entre dois pontos. A distância pode se referir ao espaço entre dois pontos estacionários (por exemplo, a altura de uma pessoa é a distância da parte inferior de seus pés até o topo de sua cabeça) ou pode se referir ao espaço entre a posição atual de um movimento objeto e sua localização inicial. A maioria dos problemas de distância podem ser resolvidos com as equações d = sgema × t onde d é a distância, sgema a velocidade média, e t o tempo, ou a equação d = √((x2 - X1) + (s2 - y1)), onde (x1, y1) e (x2, y2) são as coordenadas x e y de dois pontos.
Degraus
Método 1 de 2: Determine a distância com velocidade e tempo médios

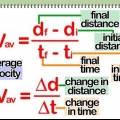
1. Determine os valores para velocidade e tempo médios. Ao tentar encontrar a distância percorrida por um objeto em movimento, duas informações são vitais para fazer esse cálculo: o Rapidez` (ou magnitude da velocidade) e oTempo onde o objeto foi movido. Com esses dados, é possível encontrar a distância percorrida pelo objeto, usando a fórmula d = sgema × t.
- Para entender melhor a aplicação da fórmula da distância, nesta seção vamos resolver um problema de exemplo. Digamos que estamos dirigindo a cerca de 120 km/h e queremos saber a distância que percorreremos em meia hora. De 120 km/h como nosso valor para a velocidade média e 0,5 horas como nosso valor para o tempo, resolveremos esse problema na próxima etapa.

2. Multiplique a velocidade média pelo tempo. Uma vez que você conhece a velocidade média de um objeto em movimento e o tempo que levou para se mover, encontrar a distância que ele percorreu é relativamente fácil. Basta multiplicar esses dois valores juntos para obter sua resposta.

3. Edite a equação para resolver as outras variáveis. A simplicidade da equação de distância básica (d = sgema × t) facilita bastante o uso da equação para encontrar os valores das variáveis além da distância. Isole a variável que deseja resolver de acordo com as regras básicas de matemática, e depois insira os valores das outras duas variáveis, para encontrar o valor da terceira. Em outras palavras, para encontrar a velocidade média do seu objeto, use a equação sgema = d/t e para encontrar o tempo que um objeto viajou, use a equação t = d/sgema.

4. Observe que a variávelgema` na fórmula da distância refere-se a média Rapidez. É importante entender que a fórmula de distância padrão fornece uma imagem simplificada do movimento de um objeto. A fórmula da distância assume que o objeto em movimento tem uma velocidade constante tem - em outras palavras, assume que o objeto em movimento está se movendo a uma velocidade `uniforme` e imutável. Para problemas matemáticos abstratos, como os encontrados em um ambiente acadêmico, às vezes ainda é possível modelar o movimento de um objeto usando essa suposição. Na vida real, no entanto, esse modelo muitas vezes não representa com precisão o movimento de objetos em movimento, que na realidade podem acelerar, desacelerar, parar e reverter ao longo do tempo.
Método 2 de 2: Determinando a distância entre dois pontos

1. Determinando dois pontos em um espaço plano. E se, em vez de determinar a distância percorrida por um objeto em movimento, você precisa determinar a distância entre dois objetos estacionários?? Em casos como este, a fórmula de distância baseada em velocidade descrita acima não será útil. Felizmente, existe outra fórmula de distância para encontrar rapidamente a distância mais curta entre dois pontos. No entanto, para esta fórmula você precisa saber as coordenadas dos dois pontos. Se você está lidando com uma distância unidimensional (como em uma reta numérica), suas coordenadas são dois números, x1 e x2. Se você está lidando com distância em duas dimensões, então você precisa de valores para dois pontos (x,y), (x1,y1) e (x2,y2). Finalmente, para três dimensões você precisa de valores para (x1,y1,z1) e (x2,y2,z2).

2. Determinar a distância em uma linha subtraindo o valor das coordenadas para os dois pontos. Calcular a distância unidimensional entre dois pontos se você souber o valor de cada ponto é fácil. Basta usar a fórmula d = |x2 - X1|. Nesta fórmula você subtrai x1 fora de x2 e pegue o valor absoluto de sua resposta para encontrar a distância entre x1 e x2 encontrar. Normalmente você usa a fórmula de distância unidimensional quando os dois pontos estão em uma linha numérica ou eixo.

3. Encontre a distância no plano usando o teorema de Pitágoras. Encontrar a distância entre dois pontos no espaço bidimensional é mais complicado do que em uma dimensão, mas não é difícil. Basta usar a fórmula d = √((x2 - X1) + (s2 - y1)). Nesta fórmula, você subtrai as duas coordenadas x, eleva o resultado ao quadrado, subtrai as coordenadas y, eleva o resultado ao quadrado, soma os dois resultados intermediários e calcula a raiz quadrada para encontrar a distância entre os dois pontos para encontrar. Esta fórmula funciona no plano bidimensional — por exemplo, nos gráficos padrão x/y.

4. Determine a distância tridimensional alterando a fórmula da área. Em três dimensões, os pontos também têm uma coordenada z além das coordenadas x e y. Para encontrar a distância entre dois pontos no espaço tridimensional, use d = √((x2 - X1) + (s2 - y1) + (z2 - z1)). Esta é uma forma modificada da fórmula de distância bidimensional descrita acima que também leva em conta as coordenadas z. Ao subtrair as duas coordenadas z uma da outra, elevá-las ao quadrado e percorrer o resto da fórmula conforme descrito acima, você tem certeza de que sua resposta final reflete a distância tridimensional entre os dois pontos.
Artigos sobre o tópico "Calcular distância"
Оцените, пожалуйста статью
Popular