Também não se esqueça de conectar o ponto inicial com o ponto final, usando uma linha reta.Este é o deslocamento que vamos calcular. Por exemplo, se um objeto viaja primeiro 300 metros na direção leste e depois 400 metros na direção norte, um triângulo retângulo é formado. AB é o primeiro lado e BC é o segundo lado do triângulo.AC é a hipotenusa do triângulo e seu valor é o deslocamento do objeto. Neste exemplo, as duas direções são "leste" e "norte." 
Por exemplo, x = 300 e y = 400.Sua equação agora fica assim: s = √300² + 400². 
Por exemplo: s = √90000 + 160000.s = √250000.s = 500.Agora você sabe que o deslocamento é igual a 500 metros. 

A equação ficará assim: s = 1/2(20 + 23)45. 
Para esta equação, não importa muito se você acidentalmente trocar as velocidades inicial e final. Porque você soma esses valores primeiro, não importa. Mas em outras equações, trocar as velocidades inicial e final pode afetar a resposta final, ou o valor do deslocamento. Sua equação agora fica assim: s = 1/2(43)45.Primeiro divida 43 por 2, o que dá 21,5 como resposta. Multiplique 21,5 por 45, que dá 967,5 metros como resposta.967,5 é o deslocamento do carro, visto do ponto de partida. 

Com base no exemplo acima, sua equação agora deve ficar assim: s = 25(4) + 1/2(3)4².Certamente pode ajudar se você colocar parênteses em torno dos valores de aceleração e tempo para manter os números separados uns dos outros. 
Vamos dar uma olhada mais de perto na equação: s = 25(4) + 1/2(3)4². A ordem é: 4² = 16; então 16 x 3 = 48; então 25 x 4 = 100; e se último 48/2 = 24. A equação agora se parece com isso: s = 100 + 24.Após a adição, isso dá s = 124, então o deslocamento é de 124 metros. 

Um exemplo de tarefa: uma garota está sentada em um carrossel. Seu assento está a uma distância de 1 metro do centro do círculo (o raio). Se a menina se move ao longo de um arco circular de 1,5 metro (deslocamento linear), qual é seu deslocamento angular? A equação fica assim: θ = 1,5/1. 
Após a divisão 1.5/1 você fica com 1.5.O deslocamento angular da menina é 1,5 radianos. Como o deslocamento angular indica o quanto um objeto foi girado a partir de sua posição inicial, é necessário representá-lo em radianos, não como uma distância. Os radianos são unidades usadas para medir ângulos. 

O deslocamento também é chamado de "grandeza vetorial" referido como a mudança na posição de um objeto em comparação com a direção na qual o objeto se move. Suponha que você caminhe 5 metros para o leste. Se você caminhar 5 metros para oeste novamente, você se moverá na direção oposta, de volta ao seu ponto de partida. Mesmo que você tenha caminhado um total de 10 metros, sua posição não mudou e seu deslocamento é, portanto, de 0 metros. 
Imagine um treinador de futebol saltando para frente e para trás ao longo das linhas laterais.Ao dar instruções aos jogadores, ele percorreu a linha várias vezes, para frente e para trás. Se você ficasse constantemente de olho no treinador, veria a distância que ele percorre. Mas suponha que o treinador pare para dizer algo a um defensor? Se ele estiver em um local diferente do ponto de partida, você observa o movimento do treinador (em um determinado momento). 
Um caminho curvo eventualmente o levará do ponto inicial ao ponto final, mas esse não é o caminho mais curto. Para ajudá-lo a visualizar isso, imagine andar em linha reta e ser parado por um pilar ou outro obstáculo. Você não pode atravessar o pilar, então você o contorna. Mesmo que você acabe no mesmo lugar como se tivesse atravessado o pilar, ainda teve que percorrer um caminho mais longo para chegar lá. Embora o deslocamento seja preferencialmente em linha reta, é possível medir o deslocamento de um objeto que "Nós vamos" se move por um caminho tortuoso. Isso é chamado de "deslocamento angular" e pode ser calculado encontrando a distância mais curta que existe entre o ponto inicial e o ponto final. 
Por exemplo, suponha que você ande 5 metros para leste e depois 3 metros para oeste. Embora você esteja tecnicamente a 2 metros do seu ponto de partida, o deslocamento é -2 porque você está se movendo na direção oposta nesse ponto.A distância sempre será positiva, porque você não sabe a distância que percorreu "desfeito" pode fazer. Deslocamento negativo não significa diminuição do deslocamento. É simplesmente uma forma de indicar que o movimento está na direção oposta. 
Portanto, isso só é possível se você se mover em linha reta a partir do ponto de partida e sem mudar de direção depois.Por exemplo, suponha que você more em São Francisco, Califórnia, e consiga um emprego em Las Vegas, Nevada. Você terá que se mudar para Las Vegas para morar mais perto do trabalho. Se você pegar o avião, um voo direto de São Francisco para Las Vegas, você percorreu 670 km e seu deslocamento é, portanto, de 670 km. No entanto, se você viajar de carro de São Francisco a Las Vegas, sua distância ainda pode ser de 670 km, mas você percorreu 906 km nesse meio tempo.Como dirigir geralmente envolve uma mudança de direção (desligar, pegar um caminho diferente), você percorreu uma distância muito maior do que a distância mais curta entre as duas cidades.
Calcular deslocamento
Contente
O termo deslocamento na física refere-se à mudança em vez de um objeto. Ao calcular o deslocamento, você mede quanto um objeto se moveu, com base nos dados da posição inicial e da posição final. A fórmula que você usa para determinar o deslocamento depende das variáveis que são dadas para um problema. Siga os seguintes passos para aprender a calcular o deslocamento de um objeto.
Degraus
Parte 1 de 5: Calculando o deslocamento resultante

1. Use a fórmula para o deslocamento resultante usando a unidade de comprimento usada para especificar a posição inicial e final. Embora a distância seja diferente do deslocamento, uma declaração sobre o deslocamento resultante indicará quanto "metro" descartou um objeto. Use essas unidades de medida para calcular o deslocamento, a distância de um objeto de sua localização original.
- A equação para o deslocamento resultante é: s = √x²+y²."s" significa deslocamento.X é a primeira direção em que o objeto se move e y é a segunda direção em que o objeto se move. Se o seu objeto se move apenas em 1 direção, então y = 0.
- Um objeto só pode se mover em no máximo 2 direções, porque mover-se ao longo da linha norte-sul ou da linha leste-oeste é considerado neutro.

2. Conecte os pontos de acordo com a ordem do movimento e rotule esses pontos de A a Z.Use uma régua para desenhar linhas retas de ponto a ponto.

3. Insira os valores para x² e y².Agora que você sabe a direção em que seu objeto está se movendo, você pode começar a preencher os valores das variáveis relevantes.

4. Trabalhe a equação. Calcule primeiro 300² e depois 400², some-os e subtraia a raiz quadrada da soma.
Parte 2 de 5: Conhecendo o vetor velocidade e a duração do tempo

1. Use esta fórmula se o problema fornecer o vetor velocidade e a duração do tempo. Pode acontecer que um problema de física não diga uma palavra sobre a distância percorrida, mas indique quanto tempo um objeto está viajando e a que velocidade. Você pode então calcular o deslocamento usando a duração do tempo e a velocidade.
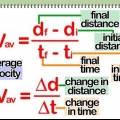
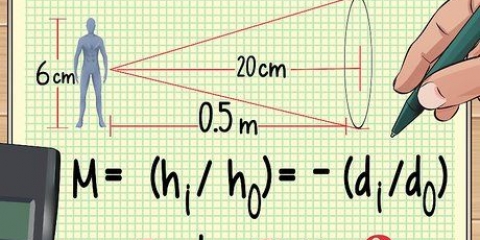
- Nesse caso, a equação ficará assim: s = 1/2(u + v)t.u = a velocidade inicial do objeto, a velocidade na qual o objeto começou a se mover em uma determinada direção.v = a velocidade final do objeto, ou quão rápido ele foi no final. t = a quantidade de tempo que o objeto levou para chegar ao seu destino.
- Por exemplo: Um carro dirige por 45 segundos.O carro virou para oeste com velocidade de 20 m/s (velocidade inicial) e no final da rua a velocidade é de 23 m/s (velocidade final). Calculou o deslocamento com base nesses dados.

2. Insira os valores para a velocidade e o tempo. Agora que você sabe quanto tempo o carro está dirigindo e qual foi a velocidade inicial e final, você pode encontrar a distância do ponto inicial ao ponto final.

3. Elabore a equação depois de inserir os valores. Lembre-se de calcular os termos na ordem correta ou o deslocamento dará errado.
Parte 3 de 5: Quando velocidade, aceleração e tempo são dados

1. Outra equação é necessária se a aceleração for dada para um problema, juntamente com a velocidade e o tempo. Com essa tarefa, você sabe qual foi a velocidade inicial do objeto, qual é a aceleração e há quanto tempo o objeto está na estrada. Você precisa da seguinte equação.
- A equação para este tipo de problema é assim: s = ut + 1/2at².O "vocês" ainda representa a velocidade inicial; O "uma" é a aceleração do objeto, ou também a rapidez com que a velocidade do objeto muda. A variável"t" pode significar o tempo total ou pode indicar um período específico em que o objeto acelerou. De qualquer forma, isso é indicado em unidades de tempo como segundos, horas, etc.
- Suponha que um carro com velocidade inicial de 25 m/s ganhe uma aceleração de 3 m/s2 por um período de 4 segundos.Qual é o deslocamento do carro após 4 segundos?

2. Preencha os valores no lugar correto na equação. Ao contrário da equação anterior, apenas a velocidade inicial é mostrada aqui, portanto, certifique-se de inserir os valores corretos.

3. Calcule o deslocamento resolvendo a equação. Uma maneira rápida de ajudá-lo a lembrar a ordem das operações em uma equação é o mnemônico "Sr. Dale esperando por resposta".Indica todas as operações aritméticas na ordem correta (Exagero, Multiplicação, Divisão, Quadratura, Adição e Subtração).
Parte 4 de 5: Calculando o deslocamento angular

1. Determinando o deslocamento angular quando um objeto se move ao longo de uma curva. Embora isso ainda envolva o cálculo do deslocamento usando uma linha reta, você precisa da diferença entre a posição inicial e final ao longo de um caminho curvo.
- Tomemos como exemplo uma garota que está em um carrossel. Enquanto ela gira em torno do lado de fora da roda, ela se move em um círculo. O deslocamento angular tenta encontrar a distância mais curta entre a posição inicial e final se um objeto não estiver se movendo em linha reta.
- A fórmula do deslocamento angular é: θ = S/r, através do qual "s" representa o deslocamento linear, "r" para o raio e "θ" o deslocamento angular é.Deslocamento linear é a distância que um objeto percorre ao longo de um círculo.O raio é a distância de um objeto ao centro do círculo.Deslocamento angular é o valor que queremos saber.

2. Insira os valores do deslocamento linear e do raio na equação. Lembre-se que o raio é a distância do centro de um círculo até a borda; pode ser que o diâmetro seja dado para um problema, nesse caso você terá que dividi-lo por 2 para encontrar o raio (raio) do círculo.

3. Divida o deslocamento linear pelo raio.Isso lhe dará o deslocamento angular do objeto.
Parte 5 de 5: Entendendo o deslocamento

1. É importante entender que "distância" às vezes significa outra coisa do que "deslocamento."A distância diz algo sobre o quão longe um objeto se moveu no total.
- A distância é algo que também chamamos de "escalar" mencionar. É uma maneira de indicar a distância que você percorreu, mas não diz nada sobre a direção em que você se moveu.
- Por exemplo, se você caminhar 2 metros para leste, 2 metros para sul, 2 metros para oeste e novamente 2 metros para norte, você estará de volta ao seu ponto de partida. Embora você tenha percorrido uma distância total de 10 metros, seu deslocamento é igual a 0 metros, porque seu ponto final é igual ao seu ponto inicial.

2. Deslocamento é a diferença entre dois pontos. O deslocamento não é uma soma de movimentos como é o caso da distância; trata-se apenas da parte entre o ponto inicial e o ponto final.

3. Lembre-se bem das palavras "vai e volta" quando você tenta imaginar um deslocamento. A direção oposta desfaz o movimento na direção original.

4. O deslocamento é medido ao longo de uma linha reta, não ao longo de um caminho circular. Para descobrir o movimento, você procura o caminho mais curto entre dois pontos diferentes.

5. Por favor, entenda que o deslocamento também pode ter um valor negativo, ao contrário da distância. Se o ponto final for alcançado movendo-se em uma direção oposta à direção que você começou (em relação ao ponto inicial), seu deslocamento é negativo.

6. Perceba que os valores de distância e deslocamento às vezes podem ser os mesmos. Se você andar em linha reta por 25 metros e depois parar, a distância percorrida é igual ao deslocamento, simplesmente porque você não mudou de direção.
Pontas
- Trabalhe com precisão
- Não memorize as fórmulas, mas tente entender como elas funcionam
Necessidades
- Calculadora
- Medidor de distância
Artigos sobre o tópico "Calcular deslocamento"
Оцените, пожалуйста статью
Popular