Deslocamento = d Deslocamento é a distância que um determinado objeto percorreu. Normalmente a unidade de deslocamento é anotada em metros. Tempo = t Velocidade = v A velocidade vetorial é a velocidade de um objeto em uma determinada direção. Ao calcular a velocidade instantânea, estamos procurando a velocidade de um objeto em um dado instante t (tempo). A velocidade é geralmente observada em metros por segundo (m/s). Inclinação (ou "declive") = m Aqui pode ser útil mostrar o movimento de um objeto em um gráfico x-y simples com tempo plotado ao longo do eixo x e deslocamento ao longo do eixo y. Então a inclinação da linha em um certo ponto é a velocidade do objeto. 
A velocidade (v) em um determinado momento (t) é igual à inclinação (taxa de variação) da equação acima, onde o deslocamento (d) é plotado em relação ao tempo (t). 
Uma regra geral para encontrar a derivada: Se y = a*x, então a derivada é a*n*x. Esta regra é aplicada a qualquer termo do polinômio. A constante (o número sem uma variável ao lado) desaparecerá porque é multiplicado por 0. 






Para calcular a velocidade instantânea é necessário calcular a inclinação de um gráfico para qualquer ponto dado. 




O valor para o qual a inclinação se move quando H se aproxima de 0 é o limite. Isso é igual à inclinação da tangente à curva. A tangente é uma linha reta definida como uma paralela à parábola em uma distância infinitamente curta. A inclinação da linha tangente é, portanto, a inclinação da parábola/curva se H se torna uma distância infinitesimal na linha. A equação para encontrar a tangente é a derivada da equação da função deslocamento, como na parte um. 
Calcular velocidade instantânea
Contente
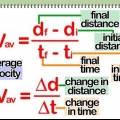
A velocidade vetorial (velocity em inglês) é definida como a velocidade de um objeto em uma determinada direção. Para fins gerais, encontrar a velocidade de um objeto é tão simples quanto dividir a distância percorrida pelo tempo que leva para percorrer essa distância. Mas isso só dá a velocidade média ao longo de um determinado caminho. Usando equações matemáticas e derivadas, é possível calcular a velocidade do objeto a qualquer momento ao longo do caminho. Isso é chamado velocidade instantânea. Por uma questão de conveniência e legibilidade, vamos nos referir à velocidade a seguir, tanto quando nos referimos à velocidade `normal` quanto à velocidade vetorial.
Degraus
Método 1 de 2: Calculando a velocidade instantânea

1. O que é "velocidade instantânea". Objetos que se movem podem fazer isso com um velocidade constante – que está se movendo a uma velocidade constante durante toda a viagem. Um corredor correndo ao longo de um campo de futebol mantém aproximadamente a mesma velocidade em todo o comprimento do campo. Os objetos também podem se mover com um velocidade variável. Por exemplo, um carro dirigindo em uma estrada com muitas curvas não terá a mesma velocidade o tempo todo – nas curvas a velocidade diminui, só para aumentar novamente nas retas.
- Velocidade instantânea é uma medida da velocidade de um objeto em qualquer ponto no tempo. Por exemplo, a velocidade instantânea de um foguete exatamente um segundo após a ignição do propelente é muito menor do que sua velocidade instantânea 30 segundos após a decolagem, se o foguete teve tempo para ganhar velocidade.

2. Conheça suas variáveis. Ao lidar com cálculos de velocidade instantânea, você quase sempre encontrará certas variáveis em algum ponto. Essas variáveis são:

3. Um exemplo. Digamos que o deslocamento de um objeto pode ser representado por uma equação: deslocamento(s) = 3t + 4t + 7. O gráfico desta função é uma linha curva ou parábola, onde o eixo x representa o tempo e o eixo y representa o deslocamento.

4. Para calcular a velocidade instantânea de um objeto com um deslocamento de acordo com a função acima, precisamos da derivada desta função. A derivada de uma função é igual à inclinação da função em qualquer ponto do gráfico. Para encontrar a derivada, derivamos a função de acordo com esta fórmula:

5. Use esta fórmula para calcular a derivada da função. Se escrevermos isso como y = 3x + 4x + 7, então a derivada é (3*2)*x+(4*1)*x+(7*0)*x

6. Simplifique a equação. Multiplicando todos os termos entre parênteses dá 6x+ 4x+ 0x

7. Continue simplificando. Esta equação pode ser escrita como 6x + 4. O "0x" termo torna-se então igual a 0, enquanto o "4x" termo é simplificado para 4 (n = 1.)

8. Faça esta nova função igual à inclinação m. Usamos esta função derivada para encontrar a inclinação da equação original y = 3x + 4x + 7 para qualquer valor de x (tempo). A inclinação original da equação em qualquer momento é a velocidade instantânea.

9. Encontre a velocidade instantânea do objeto para t = 4 segundos. Tudo o que você precisa fazer é inserir o valor do tempo na variável x da derivada da equação. Isso dá a seguinte equação y = 6(4) + 4 . Isso é simplificado para 28. A velocidade instantânea do objeto por t = 4 segundos é 28 m/s.
Método 2 de 2: Entendendo um derivativo

1. Desenhe um sistema de coordenadas x-y comum. Para entender corretamente como uma derivada pode ajudar a encontrar a velocidade instantânea de um objeto, uma representação gráfica é muito útil. O eixo y representa o deslocamento do objeto, enquanto o eixo x representa o tempo.
- O gráfico pode continuar abaixo do eixo x. Se a linha que representa o movimento do objeto estiver abaixo do eixo x, significa que o objeto está se movendo na direção inversa e antes do ponto de partida. Normalmente, o gráfico não se estenderá além do eixo y. A velocidade não é medida para objetos que voltam no tempo!
- Se você não tem certeza de como desenhar um gráfico ou exatamente o que o eixo x e o eixo y representam, aprenda a pode desenhar um gráfico de uma função.

2. Desenhe uma linha curva, começando do ponto na linha x = 0, na direção do eixo x. A inclinação da linha é a taxa de variação de y dividida pela taxa de variação de x. Então, se y é igual ao deslocamento e x é igual ao tempo, então a inclinação é igual à velocidade.

3. Para encontrar a inclinação de uma linha para um determinado ponto, usamos um truque onde encontramos o limite da equação. Encontrar o limite requer dois pontos P e Q em uma linha curva e encontrar a inclinação da linha através de ambos os pontos à medida que a distância entre os dois pontos fica cada vez menor.

4. Escolha um ponto P na linha. Por exemplo, coloque P em x = 1. A localização exata não importa. Escolha um valor conveniente.

5. Escolha um segundo ponto Q na linha. Q deve estar a uma curta distância do P. Em nosso exemplo, Q está no ponto com x=3, enquanto P está no ponto com x=1.

6. Encontre a inclinação entre P e Q. A inclinação entre P e Q torna-se então (a diferença no valor y de P e Q)/(a diferença no valor x P e Q). Referimo-nos a essa diferença nos valores de x de P e Q como H. Neste caso H é igual a 3-1=2.

7. Faça o valor de H menor. Em outras palavras, aproxime Q de P no eixo x e, em seguida, calcule a inclinação novamente entre P e Q. Faça isso repetidamente, cada vez diminuindo a distância entre P e Q. Depois de calcular isso algumas vezes, deve ficar claro que a inclinação está se aproximando de um determinado valor. Enquanto H>0 a inclinação nunca atingirá esse valor, mas apenas se aproximará. Dizemos então que a inclinação o limite está se aproximando.

8. Use derivadas para encontrar a inclinação se H representar um intervalo infinitesimal na linha. A derivada de uma equação é encontrada por "x, é N*x" para aplicar a qualquer termo da equação original.
Pontas
- O deslocamento é como a distância, mas em uma certa direção, então o deslocamento é um vetor e a velocidade é uma grandeza escalar. O deslocamento pode ser negativo enquanto a distância só pode ser positiva.
- Para encontrar a aceleração (a variação da velocidade ao longo do tempo), use o método da primeira parte para encontrar a derivada de sua função de deslocamento. Então tire a derivada disso. Isso fornece a equação para encontrar a aceleração em qualquer ponto no tempo - tudo o que você precisa fazer é inserir o valor do tempo nesta segunda derivada.
- A equação que relaciona y (deslocamento) a x (tempo) pode ser muito simples, como por exemplo. y = 6x + 3. Neste caso a inclinação é constante e não é necessário encontrar uma derivada da inclinação. É igual a 6, de acordo com a equação linear y = mx + b.
Artigos sobre o tópico "Calcular velocidade instantânea"
Оцените, пожалуйста статью
Popular