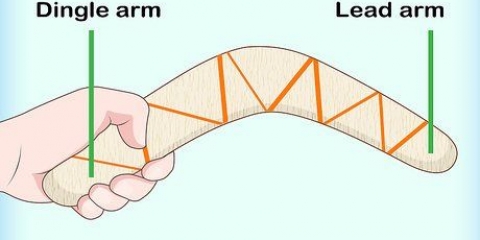
Imagine uma linha da bola branca ao cinto, cruzando em ângulo reto. Agora imagine a bola branca indo para o cinturão. Este caminho é a hipotenusa de um triângulo retângulo formado pela primeira linha e parte da banda. Agora imagine a bola branca quicando e acertando a bola objeto. Desenhe mentalmente um segundo triângulo retângulo apontando na direção oposta. 
A lei do espelho nos diz que os dois ângulos entre a hipotenusa e a banda são iguais. Ambos são triângulos retângulos, então cada um tem dois ângulos de 90º. Quando as duas bolas começaram equidistantes do pneu, sabemos que os dois lados entre a bola e o pneu são iguais. 

Os dois triângulos ainda têm os mesmos ângulos, mas não os mesmos comprimentos. Isso os torna triângulos semelhantes: mesma forma, tamanhos diferentes. Quando a bola branca está duas vezes mais longe do cinto, o primeiro triângulo é duas vezes maior que o segundo triângulo. Isso significa que o `lado da banda` do primeiro triângulo é duas vezes maior que o `lado da banda` do segundo triângulo. Apontar para um ponto na banda ⅔ do caminho para a bola objeto, já que ⅔ é duas vezes maior que ⅓. 

Um golpe direto sobrepõe completamente a outra bola. Você poderia dizer que tem uma `plenitude` de 1. Se a bola branca cobrir ¾ da bola objeto, é um acerto crítico de ¾. 
Um golpe direto resulta em um ângulo de corte de 0º. A bola objeto continua no mesmo caminho que a bola branca. Um tiro de ¾ envia a bola objeto em um ângulo de 14,5º. Um ½ tiro envia a bola objeto em um ângulo de 30º. Um tiro de ¼ envia a bola objeto em um ângulo de 48,6º. 

Crie um segmento de linha reta do bolso até o centro da bola objeto. Estenda esta linha um pouco além da bola objeto. Imagine uma `bola fantasma` neste local, bem nesta linha e tocando a bola objeto. Para acertar a bola objeto no bolso, você deve apontar para o centro da `bola fantasma`. 
Por exemplo, se o ângulo com a bola A for de cerca de 45º, então o ângulo de corte (o ângulo de corte) que você deseja alcançar é de cerca de 15º. A regra de sobreposição acima nos diz que uma colisão completa de ¾ deve produzir esse ângulo. 


100% inglês ou inglês máximo significa que você acerta a meio caminho entre o centro e a borda da bola. Este é o mais distante do centro que você pode evitar colidir e saltar de forma confiável. 50% inglês significa que você acerta a meio caminho entre o ponto máximo e o centro da bola (¼ do centro até a borda da bola). Você pode usar qualquer outra porcentagem de inglês acertando pontos diferentes entre o ponto médio e o ponto máximo. 
O termo vem da analogia de duas engrenagens que se encaixam suavemente e transferem perfeitamente o movimento. 
Se o ângulo de corte for 15º, use um pouco mais de 20% de rotação lateral. (Lembre-se de que o ângulo de interseção é o ângulo entre a trajetória original da bola branca e a trajetória da bola objeto). Se o ângulo de corte for de 30°, use 40% de rotação lateral. Se o ângulo de corte for de 45º, use cerca de 55% de rotação lateral. Se o ângulo de corte for 60º, use cerca de 70% de rotação lateral. Quando o ângulo de corte se aproxima de 90º, use 80% de rotação lateral. 
Esse efeito é chamado de `lançamento induzido por corte`: o ângulo de corte transferiu um giro que trouxe a bola para a trajetória esperada. Você pode usar isso a seu favor para fazer fotos aparentemente impossíveis. Se o seu único chute claro levar a bola um pouco para a direita, use mais inglês externo para colocar a bola na caçapa.
Jogue sinuca como um matemático
Contente
Bolas de bilhar colidem com elasticidade quase perfeita. Isso significa que a energia cinética em seu movimento é quase completamente conservada e muito pouco dela se dissipa em calor ou outros transportadores de energia. Isso torna a sinuca e o bilhar ótimos esportes para analisar matematicamente. Se você tem controle perfeito sobre como você acerta a bola de bilhar e onde você quer, você sempre pode prever o que vai acontecer.
Algumas dicas
- Uma bola batendo em um pneu no canto X também irá ricochetear no pneu no mesmo canto X (se não houver giro).
- Se a bola branca e a bola objeto estiverem equidistantes de um pneu, você pode acertar a bola objeto mirando no ponto do pneu que está exatamente entre as duas bolas.
- Se a bola branca está X vezes mais distante do pneu que a bola objeto, imagine duas linhas perpendiculares estendendo-se do pneu até as duas bolas. Aponte para um ponto na fita,
a distância da linha da bola objeto.
- Método da bola fantasma para arremessos de canto: desenhe uma linha da caçapa até a bola objeto. Imagine que uma bola fantasma atinge a bola objeto e fica nesta linha. Mire no centro da bola fantasma.
Degraus
Parte 1 de 3: Prevendo o ângulo em que uma bola quicará no pneu

1. Entenda a lei da reflexão. Muitos jogadores de sinuca já conhecem esta simples lição de matemática, pois ela ocorre toda vez que você joga a bola branca de um pneu. Esta lei diz que o ângulo em que a bola atinge o pneu é igual ao ângulo em que a bola quica. Em outras palavras, se a bola se aproximar do pneu em um ângulo de 30º, ela também irá quicar em um ângulo de 30º.
- A lei do espelho originalmente se refere ao comportamento da luz. A regra aqui é que `o ângulo de incidência é igual ao ângulo de reflexão`.

2. Coloque a bola branca e a bola objeto equidistantes do cinto. Nesse cenário, o objetivo é tirar a bola branca da faixa e fazê-la retornar para acertar a bola objeto. Agora, resolva isso na forma de um problema geométrico:

3. Prove que os dois triângulos são congruentes. Neste caso, podemos usar a regra `canto-canto-lado`. Se ambos os triângulos têm dois ângulos iguais e um lado igual (na mesma forma), então os dois triângulos são congruentes. (Em outras palavras, eles são da mesma forma e tamanho). Podemos provar que esses triângulos satisfazem as condições:

4. Apontar para a parte do meio da banda. Como os dois triângulos são congruentes, os dois lados que se encontram ao longo da faixa também são iguais entre si. Isso significa que o ponto em que a bola branca toca o pneu é igual às duas posições iniciais da bola. Aponte para este ponto central quando as duas bolas estiverem equidistantes da banda.

5. Use triângulos semelhantes se as bolas não estiverem equidistantes do pneu. Digamos que a bola branca esteja duas vezes mais longe da banda do que a bola objeto. Você ainda pode imaginar dois triângulos retângulos formados pelo caminho ideal da bola branca e usar a geometria intuitiva para guiar o soco do taco:
Parte 2 de 3: Calculando o ângulo em que uma bola deve ser quicada

1. Aprenda o básico. A maioria dos socos no bilhar são socos de canto ou `cortes`, o que significa que a bola branca não atinge a próxima bola em linha reta. Quanto menos diretamente a bola branca atingir a outra bola, maior será o ângulo que a bola objeto se moverá, em relação à trajetória da bola branca.

2. Estime o imediatismo da colisão. Uma excelente maneira de estimar esse efeito é olhar ao longo da trajetória planejada da bola branca. No momento do impacto, quanto a bola branca vai `sobrepor` a bola objeto da sua perspectiva? A resposta diz o quão `cheia` a colisão é:

3. Prever o ângulo com base no grau de sobreposição. O gráfico dessas duas magnitudes não é bem linear, mas próximo o suficiente para estimar adicionando 15º cada vez que você subtrair ¼ de sobreposição. No entanto, você também pode usar essas medidas mais precisas:

4. Cuidado com chutes muito indiretos. Além de ¼ de sobreposição, torna-se difícil até estimar quanto da bola está sendo rebatida. Mais importante, o ângulo de corte está ficando mais acentuado, então pequenos erros podem ter grandes consequências. Esses tiros de perto exigem muita prática e boa técnica, mesmo depois de descobrir para onde mirar. Se puder, procure outra foto que possa tirar.

5. Mire com o método da bola fantasma em vez disso. Se a descrição da sobreposição não ajudar, tente o `método da bola fantasma`:

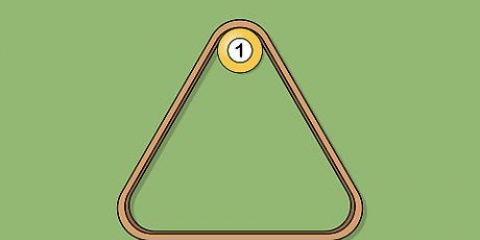
6. Siga a regra dos terços para `kiss-shot`. Um tiro de beijo está batendo na bola branca com a bola A para que ela possa acertar a bola B. Se você joga um jogo onde isso é permitido, não se esqueça desta regra: se a bola A tocar o pneu, então o corte desejado é ⅓ do ângulo formado pelas três bolas.
Parte 3 de 3: Usando o inglês (giro lateral)

1. Aperfeiçoe seu soco primeiro. Golpes e pontaria consistentes devem ser sua prioridade número um se você quiser levar o bilhar a sério. O inglês é uma técnica muito útil, mas tem efeitos complexos que exigem prática consistente.
- Será difícil limitar os efeitos do inglês (side spin) se você não tiver controle sobre a quantidade de overspin e slip. Esses efeitos são determinados pela altura em que você acerta a bola branca. O deslizamento é completamente evitado a 2/5 da distância entre o centro e o topo da bola, mas na prática 1/5 dessa distância é geralmente uma medida melhor de controle e velocidade ideais.

2. Evite o inglês se você correr o risco de afundar a bola branca. Enquanto não houver inglês, a bola branca parará após uma colisão frontal perfeita. Pratique impactos frontais com o taco no centro do eixo horizontal da bola. Uma vez que você consiga fazer a bola branca parar toda vez, você terá controle suficiente para introduzir o inglês em seu jogo.

3. Pratique o inglês em graus variados. Existem diferentes tipos de inglês, mas este artigo cobre apenas a forma mais básica. Se o seu taco acertar a bola branca à esquerda do centro, a bola vai girar ao longo deste eixo - isso é chamado de `inglês esquerdo`. Quando esta bola giratória atinge uma superfície, o giro fará com que a bola vá mais para a esquerda do que uma bola sem um inglês. Da mesma forma, acertar o lado direito resulta em `inglês certo` e a bola se move mais para a direita. Quanto mais longe do centro você estiver, mais dramático será esse efeito:

4. entender a engrenagem. Quando duas bolas colidem, a bola objeto começa a girar em torno de um certo eixo determinado pelo ângulo e quantidade de rotação lateral. Quando você atinge a engrenagem, essa rotação acontece ao longo do eixo de movimento. Em outras palavras, o movimento da bola objeto não é afetado pela rotação. Ele passará exatamente ao longo da `linha central` (a linha imaginária entre os centros das duas bolas no momento do impacto).

5. Ajuste sua rotação lateral antes de cortar. Depois de mirar seu tiro de canto usando as abordagens de sobreposição ou `fantasma`, conforme descrito na última seção, você quer ter certeza de que a bola objeto não tenha uma torção estranha e arruine seu tiro. Aqui os dados podem poupar muita tentativa e erro. Todos os números abaixo são para `fora do inglês`, o que significa mover o taco para o lado da bola branca que está mais longe da bola objeto.

6. Conheça os efeitos de uma colisão sem engrenagem. Se você usar menos rotação lateral, em seguida, a engrenagem, conforme mencionado na última etapa, a bola branca deslizará para frente no impacto, transferindo a rotação lateral para a bola objeto. A bola objeto se moverá ligeiramente para a direita do ângulo de corte esperado. Se você usar Lago rotação lateral e, em seguida, engrenagem, a bola objeto se moverá ligeiramente para a esquerda do ângulo de corte esperado.
Pontas
- Se a bola objeto estiver contra o cinto e você quiser empurrá-la no bolso ao longo do cinto, certifique-se de que a bola branca sempre toque o cinto primeiro e depois a bola objeto. Desta forma, a bola branca dá um impulso ao longo da faixa, em vez de dentro dela. (Se o ângulo de colisão for maior que 45º, você também deve usar o giro lateral.)
- Quanto maior o ângulo de colisão entre duas bolas, menos momento é transferido. Isso significa que você precisa de um soco um pouco mais forte para um atalho (um impacto de ângulo extremo).
- Após uma colisão, o ângulo entre a trajetória da bola branca e a trajetória da bola objeto será sempre igual a 90º. Use esse conhecimento para evitar que a bola branca afunde. Observe que o giro extremo pode quebrar essa regra, como acontece com bolas de bilhar de massa desigual (como as que você pode encontrar em algumas mesas de lançamento de moedas).
Avisos
- Pessoas e bolas brancas colidem com espetacular inelasticidade. Deixe essa experiência para os profissionais.
Artigos sobre o tópico "Jogue sinuca como um matemático"
Оцените, пожалуйста статью
Popular