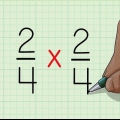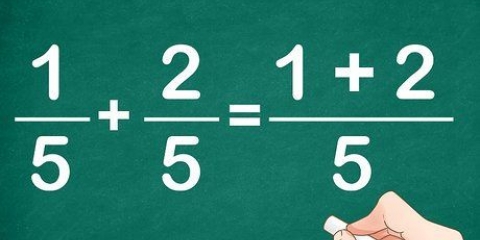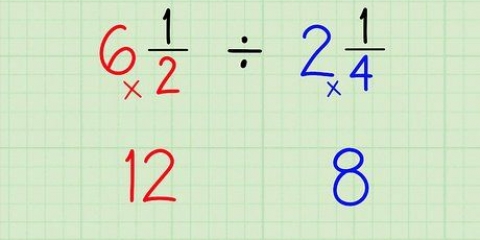Então, suponha que temos 1/2 x 3/4, então multiplicamos da seguinte forma: 1 x 3 e 2 x 4.A resposta é então 3/8. 


Se o problema era 8/15 ÷ 3/4, agora será 8/15 x 4/3. 
8 x 4 = 32 e 15 x 3 = 45, então a resposta é 32/45. 

Em nosso exemplo, isso se torna: 3 x 5 = 15.

No nosso exemplo: 15 + 2 = 17 
No nosso caso, isso se torna: 17/5. 

Determine quantas vezes o denominador atual vai para o mínimo múltiplo comum. Para 1/4, 4 x 3 = 12. Para 1/6, 6 x 2 = 12. Multiplique o numerador e o denominador da fração por esse número. Para ¼, você multiplica 1 e 4 por 3, o que resulta em 3/12. 1/6 x 2 = 2/12. Agora esta declaração se parece com isso: 3/12 + 2/12 ou 3/12 - 2/12. 
Então para 3/12 + 2/12 a resposta é 5/12. Para 3/12 - 2/12, é 1/12 Converta frações mistas em frações impróprias antes de começar. Pergunte ao seu professor se você deve ou não simplificar as respostas. Por exemplo, 2/5 não pode ser simplificado ainda mais, mas 16/40 pode.
Resolvendo frações
Contente
As frações às vezes parecem um pouco difíceis de resolver, mas com um pouco de prática e algum conhecimento extra isso se torna muito mais fácil. Depois de ter entendido o básico, você descobrirá que resolver frações é na verdade um pedaço de bolo.
Degraus
Método 1 de 4: Multiplicando frações

1. Verifique se você está lidando com duas frações. Estas instruções só funcionam com duas frações.Se você estiver lidando com uma fração mista, primeiro converta-a em uma fração imprópria...

2. Multiplique o numerador 1 pelo numerador 2 e multiplique o denominador 1 pelo denominador 2.
Método 2 de 4: Dividindo frações

1. Verifique se você está lidando com duas frações. Novamente, este processo SOMENTE funciona se você tiver convertido quaisquer frações mistas em frações impróprias.

2. Inverta a segunda fração. Não importa qual fração, desde que você não inverta ambas as frações.

3. Alterar o sinal de divisão para uma multiplicação.

4. Multiplique os numeradores e os denominadores.
Método 3 de 4: Convertendo frações mistas em frações impróprias

1. Converter frações mistas em frações impróprias. Frações impróprias são aquelas frações cujo numerador é maior que o denominador.(Por exemplo, 17/5.) Se você está multiplicando e dividindo, você deve converter frações mistas em frações impróprias antes de continuar a resolver o problema.
- Suponha que você tenha a fração mista 3 2/5.

2. Pegue o número inteiro (o número antes da fração) e multiplique pelo denominador.


3. Adicione essa resposta ao contador.

4. Coloque este número como um novo numerador acima da linha de fração e você terá uma fração imprópria.
Método 4 de 4: Adicionando e subtraindo frações

1. Encontre o mínimo múltiplo comum dos denominadores (o número de baixo). Para somar e subtrair frações, você começa com o mesmo. Encontre o menor número que se encaixa em ambos os denominadores.
- Por exemplo, se você pegar as frações 1/4 e 1/6, o mínimo múltiplo comum é 12. (4x3=12, 6x2=12)

2. Multiplique as frações dependendo do mínimo múltiplo comum. Lembre-se, você não está alterando a fração, apenas como ela é expressa. Pense em uma pizza - 1/2 ou 2/4 de uma pizza é a mesma quantidade de pizza, apenas expressa de forma diferente.

3. Adicione ou subtraia os dois numeradores (número superior), mas NÃO os denominadores.Isso não é permitido porque você deseja calcular quanto dessa fração você tem no total. Se você também incluir os denominadores, as frações mudarão.
Pontas
- Certifique-se de dominar bem as habilidades matemáticas básicas (adição, subtração, multiplicação e divisão), para que os cálculos não demorem desnecessariamente e sejam difíceis.
- O recíproco de um inteiro é colocar esse número como denominador em uma fração, com 1 como numerador. Por exemplo, 5 então se torna 1/5.
- Você pode multiplicar e dividir frações mistas sem convertê-las em frações impróprias primeiro. Mas então você precisa de outras habilidades matemáticas, e o cálculo se torna muito mais complexo. Portanto, geralmente é melhor seguir a rota das frações impróprias.
- Lembre-se: Dividir é o mesmo que multiplicar pelo recíproco.
- Quando você toma o inverso de um número negativo, o sinal de menos permanece no numerador.
Avisos
- Pergunte ao seu professor se você deve converter frações impróprias em frações mistas.
- Por exemplo, 3 1/4 em vez de 13/4.
Artigos sobre o tópico "Resolvendo frações"
Оцените, пожалуйста статью
Popular