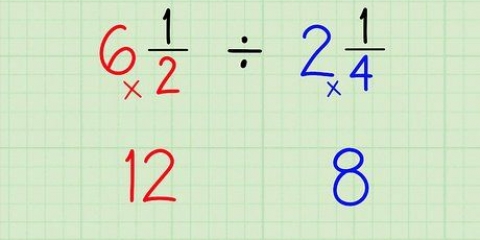18 ÷ 3 = 6, então 2/3 = (2x6)/(3x6)=12/18 18 ÷ 6 = 3, então 5/6 = (5x3)/(6x3)=15/18 18 ÷ 3 = 6, então 1/3 = (1x6)/(3x6)=6/18 

6/18 = (6 6)/(18 ÷ 6) = 1/3 18/12 = (12 6)/(18 ÷ 6) = 2/3 15/18 = (15 3)/(18 ÷ 3) = 5/6 A resposta é "1/3, 2/3, 5/6" 

Isso é chamado de multiplicação cruzada, porque você está multiplicando números na diagonal. 



Lembre-se de sempre colocar o produto da multiplicação ao lado da fração cujo numerador você usou. 
3/5=(3x3)/(5x3)=9/15 2/3=(2x5)/(3x5)=10/15 15/09 é menor que 15/10 Então 3/5 é menor que 2/3 

8/3 = 2 + 2/3 9/9 = 1 19/4 = 4 + 3/4 13/6 = 2 + 1/6 
1 é o menor 2 + 2/3 e 2 + 1/6 (ainda não sabemos qual é maior que o outro) 4 + 3/4 é o maior 
2/3 = (2x2)/(3x2) = 4/6 1/6 = 1/6 4/6 é maior que 1/6 2 + 4/6 é maior que 2 + 1/6 2 + 2/3 é maior que 2 + 1/6 

Ordenar frações por tamanho
Contente
Embora seja fácil ordenar números inteiros como 1, 3 e 8 por tamanho, nem sempre é óbvio com frações. Se todos os denominadores forem iguais, você pode ordená-los como números inteiros, por exemplo. 1/5, 3/5 e 8/5. Em outros casos, você pode converter as frações para que tenham o mesmo denominador, sem alterar o valor da fração. Isso fica mais fácil com a prática e você pode usar alguns truques úteis, tanto ao comparar duas frações quanto ao ordenar frações onde o numerador é maior que o denominador, as frações impróprias como 7/3.
Degraus
Método 1 de 3: Ordenando qualquer número de frações

1. Encontre um denominador igual para todas as frações. Use um dos seguintes métodos para encontrar um denominador ou diminua o número de uma fração, que você pode usar para reescrever cada fração na lista para facilitar a comparação. Isso é o que você chama de denominador comum, ou o minimo denominador comum se este for o menor possível:
- Multiplique cada denominador. Por exemplo, se você estiver comparando 2/3, 5/6 e 1/3, multiplique esses denominadores: 3 x 6 = 18. Este é um método simples, mas que geralmente resulta em um número muito maior do que os outros métodos, que são um pouco mais complicados.
- Ou liste múltiplos de cada denominador em uma coluna separada, até que um número que ocorra com mais frequência se destaque. Por exemplo, em 2/3, 5/6 e 1/3, você tem múltiplos de lista de 3:3, 6, 9, 12, 15, 18. Em seguida, uma lista de múltiplos de 6: 6, 12, 18. Porque 18 ocorre em ambas as listas, use esse número (você também pode usar 12, mas os exemplos abaixo pressupõem que você use 18).

2. Converta cada fração para que elas tenham um denominador igual. Lembre-se que se você multiplicar o numerador e o denominador de uma fração pelo mesmo número, o valor da fração permanece o mesmo. Use esta técnica com cada fração, uma de cada vez, para que cada fração tenha o mesmo denominador. Tente isso para 2/3, 5/6 e 1/3, com o denominador 18:

3. Ordene as frações pelos numeradores. Agora que todas as frações têm o mesmo denominador, elas são fáceis de comparar. Ordene-os do menor ao maior de acordo com o contador. Isso nos dá a seguinte lista: 18/6, 18/12, 18/15.

4. Retorne cada fração à sua forma original. Deixe as frações nesta ordem, mas converta-as de volta para a fração original. Você faz isso simplesmente lembrando qual fração pertence a qual ou dividindo os números superior e inferior da fração novamente:
Método 2 de 3: Ordenando duas frações com multiplicação cruzada

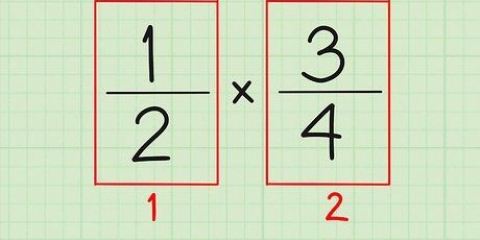
1. Escreva as duas frações lado a lado. Por exemplo, compare a fração 3/5 e a fração 2/3. Escreva estes lado a lado: 3/5 à esquerda e 2/3 à direita.

2. Multiplique o numerador da primeira fração pelo denominador da segunda. Então: 3 x 3 = 9.

3. Escreva sua resposta ao lado da primeira fração. Escreva o produto de 3 x 3 = 9, ao lado da primeira fração.

4. Multiplique o numerador do segundo fração com o denominador do primeiro. Agora para ver qual é o maior, comparamos a resposta com outra multiplicação. Multiplique esses dois números juntos. Neste exemplo (estamos comparando 3/5 e 2/3), estamos multiplicando 2 x 5.

5. Escreva a resposta ao lado da segunda fração. Escreva o resultado de 2 x 5 = 10 ao lado da segunda fração.

6. Compare os valores dos resultados. Se um valor for maior que o outro, a fração ao lado do resultado também será a maior. Então, como 9 é menor que 10, 3/5 é menor que 2/3.

7. Como, exatamente, isso funciona? O que você está fazendo é converter as frações para que ambas tenham o mesmo denominador. Então é isso que a multiplicação cruzada realmente faz! Na verdade, ele pula escrever os denominadores porque, no caso de denominadores iguais, você só precisa comparar os numeradores. Então, da seguinte forma, sem a rota curta de multiplicação cruzada:
Método 3 de 3: Ordenando frações maiores que um

1. Use este método para frações onde o numerador é maior que o denominador. Se o numerador for maior que o denominador, então esta fração é maior que 1. 8/3 é um exemplo disso. Você também pode usar isso para frações com o mesmo numerador e denominador, como 9/9. Ambos são exemplos de "impróprio" frações.
- Você ainda pode usar os outros métodos para essas frações. Este método irá ajudá-lo a entender melhor essas frações e pode ser um pouco mais rápido.

2. Converta qualquer fração imprópria em uma fração mista. Faça uma combinação de um inteiro e uma fração. Às vezes você pode facilmente fazer isso de cor. Por exemplo, 9/9 = 1. Nos casos mais complicados, use a divisão longa para descobrir quantas vezes o denominador é divisível pelo numerador. O possível restante da divisão longa permanece como uma fração. Por exemplo:

3. Ordenar os números mistos pelo número inteiro. Agora que não existem mais frações impróprias, você tem uma ideia melhor do tamanho de cada número. Ignore as frações primeiro e ordene cada número misto pelo inteiro:

4. Compare as frações em cada grupo, se necessário. Se você tiver vários números mistos com o mesmo inteiro, como 2 + 2/3 e 2 + 1/6, compare a fração de ambos os números para descobrir qual é maior. No exemplo, estamos comparando 2 + 2/3 e 2 + 1/6, convertendo as frações para o mesmo denominador:

5. Use o resultado para classificar ainda mais a lista de números mistos. A ordem de toda a lista agora se torna: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4.

6. Converta os números mistos de volta para as frações originais. Mantenha a mesma ordem, mas desfaça as alterações e reescreva as frações como as frações impróprias originais: 9/9, 8/3, 13/6, 19/4.
Pontas
- Ao sequenciar um grande número de frações, pode ser útil comparar pequenos grupos de 2, 3 ou 4 frações.
- Embora encontrar o mínimo denominador comum possa ser útil, qualquer denominador comum funcionará. Tente classificar 2/3, 5/6 e 1/3 com um denominador comum de 36 e veja se obtém o mesmo resultado.
- Se os numeradores são todos iguais, você também pode ordenar rapidamente as frações. Por exemplo, 1/8 < 1/7 < 1/6 < 1/5. Pense nisso como se fosse uma pizza: se você for de 1/2 a 1/8, você corta a pizza em 8 pedaços em vez de 2 e os pedaços são menores.
Artigos sobre o tópico "Ordenar frações por tamanho"
Оцените, пожалуйста статью
Popular