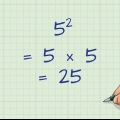Simplificando Frações Matemáticas

Contente

Degraus
Pontas
Avisos

Frações matemáticas ou algébricas parecem incrivelmente difíceis no início e podem parecer assustadoras para o aluno inexperiente. Com uma mistura de variáveis, números e até expoentes fica difícil saber por onde começar. Mas, felizmente, as mesmas regras necessárias para simplificar frações comuns, como 15/25, também se aplicam a frações matemáticas.

Degraus

Método 1 de 3: Simplificando frações

Imagem intitulada Simplifique Frações Algébricas Etapa 1

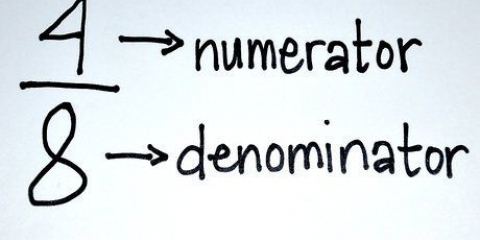
1. Conheça o vocabulário para frações matemáticas. Os seguintes termos serão usados nos exemplos e são comuns em problemas com frações:

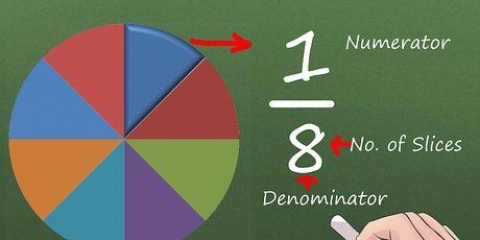
Balcão: A parte superior de uma fração (por exemplo,. (x+5)/(2x+3)).
Denominador: A parte inferior de uma fração (por exemplo,. (x+5)/(2x+3)).
Denominador comum: Este é um número pelo qual você pode dividir o numerador e o denominador de uma fração. Por exemplo, na fração 3/9, o divisor comum é 3, pois ambos os números podem ser divididos por 3.
Fator:` Um número que é multiplicado para fazer outro número. Por exemplo: os fatores de 15 são 1, 3, 5 e 15. Os fatores de 4 são 1, 2 e 4.
Equação simplificada: Todos os fatores comuns são removidos e as variáveis iguais são agrupadas (5x + x = 6x) até que você tenha obtido a forma mais simples de uma fração, equação ou problema. Se você não pode mais fazer nada com a fração, é simplificado.

Imagem intitulada Simplifique Frações Algébricas Passo 2

2. Compare como resolver frações simples. Estes são exatamente os mesmos passos que você seguirá para resolver frações matemáticas. Veja o exemplo, 15/35. Para simplificar uma fração, precisamos encontrar um denominador comum. Nesse caso, ambos os números podem ser divididos por cinco, então você pode riscar o 5 da fração:
15→5 * 3
35→5 *7
Agora você pode riscar termos semelhantes. Nesse caso, você pode riscar os dois cincos, deixando sua resposta simplificada, 3/7.

Imagem intitulada Simplifique Frações Algébricas Passo 3

3. Remova fatores de expressões algébricas como números normais. No exemplo anterior, você pode remover facilmente o 5 de 15, e o mesmo princípio se aplica a expressões mais complexas, como 15x - 5. Encontre um fator que ambos os números tenham em comum. Aqui a resposta é 5, porque você pode dividir 15x e -5 pelo número cinco. Como antes, você remove o fator comum e o multiplica pelo que está `esquerdo`.`
15x - 5 = 5 *(3x - 1) Para verificar seu trabalho, basta multiplicar os cinco de volta na nova expressão - você terminará com os mesmos números com os quais começou.

Imagem intitulada Simplifique Frações Algébricas Etapa 4

4. Agora você pode excluir termos complexos como termos simples. O mesmo princípio das frações regulares também funciona para frações matemáticas. Esta é a maneira mais fácil de simplificar frações. Pegue a fração:
(x+2)(x-3)
(x+2)(x+10)
Observe como o termo (x+2) aparece tanto no numerador (superior) quanto no denominador (inferior). Como tal, você pode removê-los para simplificar a fração algébrica, assim como removeu o 5 de 15/35:
~~(x+2)~~(x-3)→(x-3)
~~(x+2)~~(x+10)→(x+10) Isso dá a resposta final: (x-3)/(x+10).

Método 2 de 3: Simplificando frações

Imagem intitulada Simplifique Frações Algébricas Passo 5

1. Encontre um fator comum no numerador (a parte superior da fração). A primeira coisa a fazer ao simplificar uma fração algébrica é simplificar cada parte da fração. Comece com a parte de cima e risque o maior número possível de números. Como exemplo, usaremos este exercício:
9x-3
15x+6
Comece com o contador: 9x – 3. Existe um fator comum para 9x e -3, que é 3. Trabalhe os 3 colchetes externos como faria com qualquer outro número, deixando 3*(3x-1). Este é o seu novo contador:
3(3x-1)
15x+6

Imagem intitulada Simplifique Frações Algébricas Etapa 6

2. Encontrar um fator comum no denominador.Continuando o exemplo acima, isole o denominador, 15x+6. Pesquise novamente por um número que se encaixe em ambas as partes. Aqui também você pode omitir um fator de três, para que fique com 3 *(5x +2). Incorpore seu novo denominador na equação:
3(3x-1)
3(5x+2)

Imagem intitulada Simplifique Frações Algébricas Passo 7

3. Remover termos semelhantes. Este é o estágio em que você pode realmente simplificar a fração. Pegue todos os termos que estão no numerador e no denominador e remova-os. Neste caso, podemos riscar o 3 de cima e de baixo.
3(3x-1)→(3x-1)
3(5x+2)→(5x+2)

Imagem intitulada Simplifique Frações Algébricas Passo 8

4. Saiba quando a equação está completamente simplificada. Uma fração é simplificada quando não há mais fatores comuns na parte superior ou inferior. Lembre-se, você não pode remover fatores de dentro dos parênteses - no problema do exemplo, você não pode fatorar o x de 3x e 5x, porque os termos completos são na verdade (3x -1) e (5x + 2). Assim, o exemplo é completamente simplificado, com if a resposta definitiva:
(3x-1)
(5x+2)

Imagem intitulada Simplifique Frações Algébricas Passo 9

5. Experimente um exercício prático. A melhor maneira de aprender é continuar tentando simplificar frações matemáticas. As respostas estão abaixo dos problemas.
4(x+2)(x-13)
(4x+8)Responder: (x=13)
2x-x
5xResponder:(2x-1)/5

Método 3 de 3: Truques para resolver problemas mais complicados

Imagem intitulada Simplify Algebraic Fractions Step 10

1. `Inverter` frações para fatorar por números negativos. Digamos que temos a seguinte equação:
3 (x-4)
5(4-x)
Observe como (x-4) e (4-x) quase são idênticos, mas você não pode riscá-los porque eles estão invertidos. No entanto, (x - 4) pode ser escrito como -1 *(4 - x) da mesma forma que você reescreve (4 + 2x) como 2 *(2 + x). Isso é chamado de `trazer para fora dos parênteses`.
-1 *3(4-x)
5(4-x)
Agora podemos simplesmente omitir os dois idênticos (4-x):
-1 * 3~~(4x)~~
5~~(4x)~~
Disso segue a resposta final: -3/5

Imagem intitulada Simplify Algebraic Fractions Step 11

2. Reconhecer a diferença de dois quadrados enquanto trabalha. A diferença de dois quadrados é simplesmente subtrair um número ao quadrado de outro, como a expressão (a - b). A diferença de quadrados perfeitos é sempre simplificada em duas partes, adicionando e subtraindo as raízes quadradas. De qualquer forma, você pode simplificar a diferença de quadrados perfeitos assim:
a - b = (a+b)(a-b) Isso pode ser muito útil ao tentar encontrar termos semelhantes em frações matemáticas.

Exemplo: x - 25 = (x+5)(x-5)

Imagem intitulada Simplify Algebraic Fractions Step 12

3. simplificar polinômios. Polinômios ou polinômios são expressões algébricas complexas com mais de dois termos, como: x + 4x + 3. Felizmente, muitos polinômios podem ser simplificados por `fatoração`. A expressão anterior, por exemplo, pode ser reescrita como (x+3)(x+1).

Imagem intitulada Simplify Algebraic Fractions Step 13

4. Lembre-se que as variáveis também podem ser fatoradas. Isso é especialmente útil para expressões com expoentes, como x + x. Você pode omitir o maior expoente como um fator. Neste caso: x + x = x(x + 1).

Pontas

Verifique seu trabalho na fatoração multiplicando o fator de volta na equação - você obterá o mesmo número com o qual começou.
Sempre elimine os maiores números que puder para simplificar completamente sua equação.