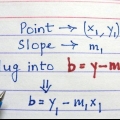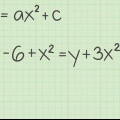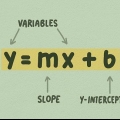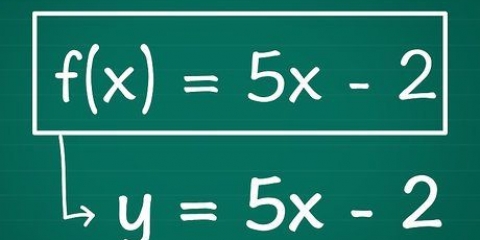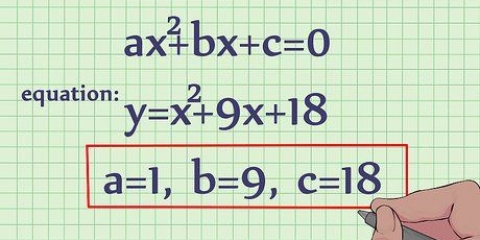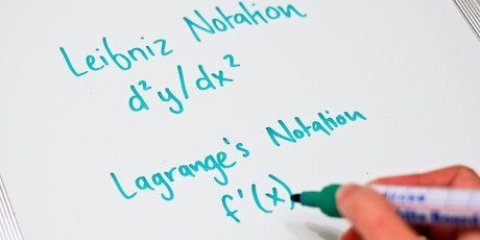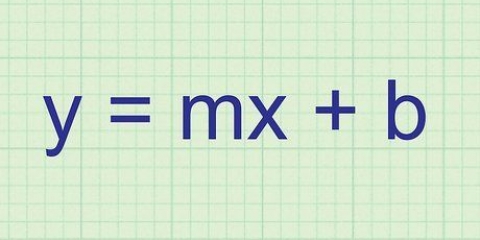Encontrando a Equação de uma Linha Tangente: 4 Passos (com Imagens)

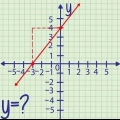
Uma tangente a uma parábola ou curva é uma linha que apenas toca a curva em um determinado ponto. Para encontrar a equação desta reta tangente, você terá que calcular a inclinação da curva nesse ponto, o que requer alguns cálculos matemáticos. Você pode então escrever a equação da reta tangente na forma ponto-inclinação. Este artigo explica os passos a seguir.

Degraus

Imagem intitulada Encontre a equação de uma linha tangente Etapa 1

1. A equação de uma curva pode ser expressa como uma função. Encontre a derivada desta função para encontrar a equação da inclinação desta curva.

A maneira mais fácil de diferenciar a maioria dos polinômios é através da regra da cadeia. Multiplique cada equação da função por sua potência para encontrar o coeficiente desse termo na derivada e, em seguida, subtraia a potência por 1.
Exemplo: Para a função f(x) = x^3 + 2x^2 + 5x + 1, a derivada é f`(x) = 3x^2 + 4x + 5.
Para f(x) = (2x+5)^10 + 2*(4x+3)^5, a derivada é f`(x) = 10*2*(2x+5)^9 + 2*5*4 *(4x+3)^4 = 20*(2x+5)^9 + 40*(4x+3)^4.

Imagem intitulada Encontre a equação de uma linha tangente Etapa 2

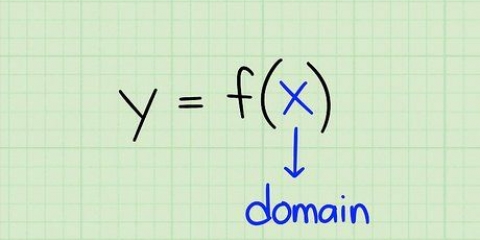
2. Se tudo estiver bem, as coordenadas onde a linha tangente encontra a curva são dadas. Insira o valor x deste ponto, na função derivada, para encontrar a inclinação da curva naquele ponto.

Para x = 2, o ponto na curva é (2,27) porque f(2) = 2^3 + 2*2^2 + 5*2 + 1 = 27.

Para f`(x) = 3x^2 + 4x + 5, a inclinação está em (2,27) é f`(2) = 3(2)^2 + 4(2) + 5 = 25.

Imagem intitulada Encontre a equação de uma linha tangente Etapa 3

3. Esta inclinação é também a inclinação da linha tangente. Agora você tem a inclinação e o ponto desta linha, então você pode escrever a equação da linha na forma ponto-inclinação, ou y - y1 = m(x - x1).

Na forma ponto-inclinação, é m a inclinação e (x1,y1) são as coordenadas do ponto. Então, neste exemplo, a equação se torna y - 27 = 25(x - 2).

Imagem intitulada Encontre a equação de uma linha tangente Passo 4

4. Também pode ser necessário converter esta equação para outra forma para obter a resposta final, caso as instruções que acompanham o problema o exijam.