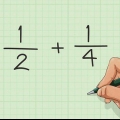Quer você escreva 1/5 + 2/5 ou 1+2/5, a resposta é a mesma: 3! Finalmente, 1 + 2 = 3. 
Então, seguindo o mesmo exemplo, o denominador é 5. Isso é tudo! Este é o número inferior da fração e metade da resposta! 
Qual foi o contador? 3. E o denominador? 5. Então, 1/5 + 2/5, ou 1 + 2/5, é igual 3/5. 

Então 2/3 se torna 2/3 x 4 e 3/4 se torna 3/4 x 3. Isso significa que agora temos 12/02 e 12/03. Mas ainda não terminamos! Você notará que, neste caso, os denominadores foram multiplicados. Isso funciona nesta situação, mas nem sempre. Às vezes você terá que procurar números menores para encontrar o LCF. E em outros casos, com números pequenos, basta multiplicar os denominadores. 
Tínhamos 2/3x4 e 3/4x3 como nosso primeiro passo - para adicionar o segundo passo, na verdade são 2 x 4/3 x 4 e 3 x 3/4 x 3. Isso significa que 12/08 e 12/09 são nossos novos números. Perfeito! 
Neste exemplo vale: 8+9/12 = 17/12. Para converter isso em um número misto, subtraia o denominador do numerador e veja o que resta. Ou seja, neste caso, 17/12 = 1 5/12 

Vamos determinar quais são os múltiplos de 12 e 8. Qual é o menor número em que ambos os números se encaixam?? 24. 8, 16, 24 e 12, 24 – bingo! 
Então 13 x 2/12 x 2 = 26/24. E 17 x 3/8 x 3 = 51/24. Percorremos um longo caminho para resolver o problema! 
26/24 + 51/24 = 77/24. Essa é a pausa que você estava procurando! Mas o balcão é bem grande.... 
Para este exemplo: 24 vai para 77. 3 vezes.Então, 24 x 3 = 72. Então resta um resto de 5! Então, qual é a sua resposta final? 3 5/24. Isso é tudo!
Adição e subtração de frações
Contente
Adicionar e subtrair frações é uma habilidade essencial para aprender. Você encontra frações em todos os lugares da vida cotidiana, especialmente nas aulas de matemática, da escola primária à universidade. Basta seguir os passos abaixo para aprender a somar e subtrair frações, sejam frações iguais, desiguais, mistas ou impróprias. Uma vez que você aprendeu uma maneira, todo o resto é muito mais fácil!
Degraus
Método 1 de 3: Adicionando e subtraindo frações com o mesmo denominador

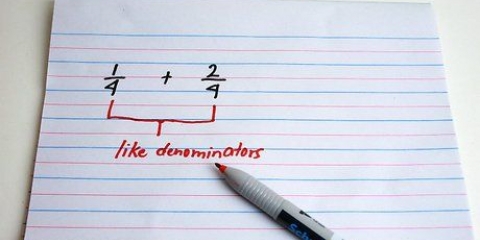
1. Escreva a equação. Se o denominador das duas frações que você adicionar/subtrair for o mesmo, inclua esse denominador na sua resposta também.
- Em outras palavras, você não precisa escrever 1/5 e 2/5 como 1/5 + 2/5 = ? Isso pode ser notado como (1+2)/5 = ?. O denominador é o mesmo e, portanto, só precisa ser mencionado uma vez. Ambos os numeradores estão acima da linha de pontuação.

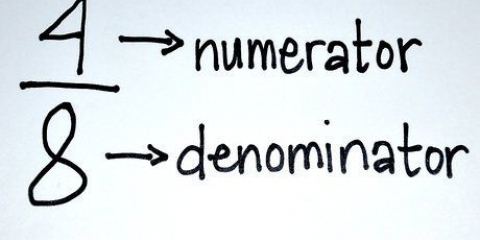
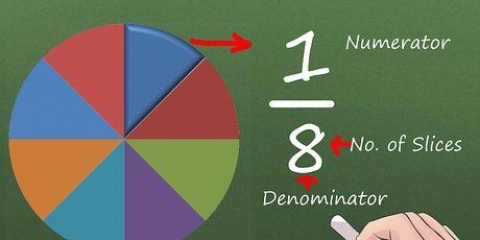
2. Adicione os contadores juntos. O numerador é o número acima da linha de fração. Veja o seguinte exemplo: 1/5 e 2/5; aqui estão 1 e 2 nossos contadores.

3. Deixe o denominador inalterado. Nada para adicionar, subtrair, etc, mas inalterado.

4. Anote a resposta. Agora tudo que você tem a fazer é escrever a resposta! Você verá que de acordo com o exemplo anterior, a resposta é 3/5.
Método 2 de 3: Adicionando e subtraindo frações com denominadores diferentes

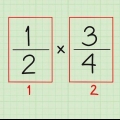
1. Encontre o Mínimo Múltiplo Comum (MLC) dos denominadores. Este é o menor número que ambos os denominadores têm em comum. Pegue as frações 2/3 e 3/4. Quais são os denominadores? 3 e 4. Para encontrar o LCF de ambos, use uma das 3 maneiras a seguir:
- Anote os múltiplos. Os múltiplos de 3 são 3, 6, 9, 12, 15, 18...e assim por diante. Os múltiplos de 4? 4, 8, 12, 16, 20, etc. Qual é o menor número que ocorre em ambos os conjuntos?? 12! Esse é o seu mínimo múltiplo comum ou o seu kgv.
- Fatoração em fatores primos. Se você sabe o que são fatores primos, você pode usar a fatoração. Aqui você determina com quais números primos você pode multiplicar um determinado número por meio da multiplicação "fazer". Para 3, os fatores são 3 e 1. Para 4, os fatores primos são 2 e 2. Então você multiplica esses juntos, então 3 x 2 x 2 = 12. seu kgf!
- Multiplique os dois números para obter opouco números. Em alguns casos, como este, você pode simplesmente multiplicar os dois números juntos – 3 x 4 = 12. Mas se seus denominadores são números grandes, isso não pode acontecer! Você não pode simplesmente fazer 56 x 44 e passar para 2464 como resposta! Não é errado, mas é estranho.

2. multiplique o denominador pelo número que você precisa para obter o lcg. Em outras palavras, você quer que cada denominador seja o mesmo número – o kgv. Para o nosso exemplo, isso deve ser 12. 4 x 3 = 12. Este é o denominador da nossa resposta final.

3. Multiplique o numerador por esse número também. Se você multiplicar o denominador de uma fração por um número, você também terá que multiplicar o numerador pelo mesmo número. O que fizemos na última etapa foi apenas parte da multiplicação necessária.

4. Adicione (ou subtraia) os numeradores para obter sua resposta. Para somar 8/12 a 9/12, basta somar os numeradores. Não se esqueça: você deixa o denominador sozinho. O número que você obteve com o LCF é o seu denominador final.
Método 3 de 3: Adicionando e subtraindo frações mistas e impróprias

1. Converta suas frações mistas em frações impróprias. Uma fração mista é um número inteiro com uma fração depois, como no exemplo acima (1 5/12). Uma fração imprópria é uma fração com numerador maior que denominador. Um exemplo disso é 17/12.
- Como exemplo tomamos 13/12 e 17/8.

2. Encontre o denominador comum. Lembre-se das três maneiras de encontrar o lcg dos denominadores? Determinando os múltiplos, usando fatores primos ou multiplicando os denominadores entre si.

3. Multiplique os numeradores pelos denominadores para obter a fração igual. Ambos os denominadores devem agora ser convertidos para 24. Como fazer 24 de 12? Multiplique por 2. De 8 a 24? Multiplique por 3. Mas não esqueça que você também tem que multiplicar os numeradores!

4. Adição e subtração de frações. Agora que ambas as frações têm o mesmo denominador, você pode facilmente adicionar ou subtrair ambas as frações. Lembre-se, deixe o denominador sozinho!

5. Transforme sua resposta em uma fração mista. Um numerador tão grande é um pouco estranho e dificulta ter uma ideia do tamanho da sua fração. Tudo o que você precisa fazer para resolver isso é dividir o numerador pelo denominador e usar o resto como numerador para sua nova fração composta.
Artigos sobre o tópico "Adição e subtração de frações"
Оцените, пожалуйста статью
Popular