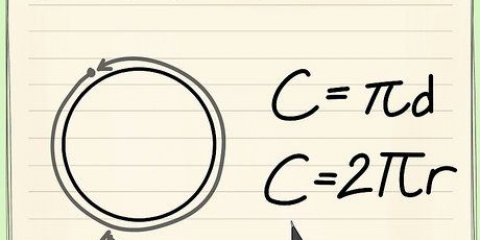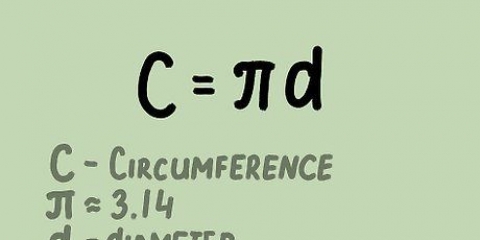Memorizando o Círculo Unitário: 14 Passos (com Imagens)

Contente

Degraus
- Parte 1 de 2: Lembre-se dos radianos
- Parte 2 de 2: Lembre-se das coordenadas x e y (cosseno, seno)
Pontas

Aprender o círculo unitário ajudará você não apenas com trigonometria e geometria, mas também com cálculo diferencial e integral. Pode parecer que você tem muito o que lembrar, mas depois de entender como funciona, você pode começar com alguns números do círculo unitário e descobrir rapidamente o resto.

Degraus

Parte 1 de 2: Lembre-se dos radianos

Imagem intitulada Memorize o Círculo Unitário Passo 1

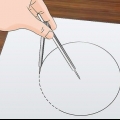
1. Desenhe duas linhas perpendiculares. Coloque uma bússola em uma grande folha de papel. Desenhe uma linha vertical e uma horizontal. Eles devem se cruzar perto do centro da página. Estes são os eixos x e y do gráfico.

Imagem intitulada Memorize o Círculo Unitário Passo 2

2. Desenhar um círculo. Usando uma bússola, desenhe um grande círculo centrado na interseção das duas linhas.

Imagem intitulada Memorize o Círculo Unitário Passo 3

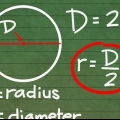
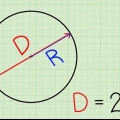
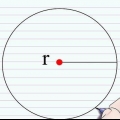
3. Entenda os radianos. Um radiano é uma medida de ângulo. É definido principalmente de tal forma que uma pessoa andando em um círculo com um Raio de 1 unidade se move em um ângulo de um radiano depois de caminhar 1 unidade ao redor do perímetro. Na próxima etapa, indicaremos os quatro pontos de coordenadas com o valor radiano. Se você se lembrar da fórmula para a relação entre a circunferência de um círculo e seu raio, poderá resolvê-la rapidamente, mas mesmo que não se lembre.

As medições em radianos do círculo unitário sempre assumem que você começa do ponto (0, 1). Para deixar claro a que ponto estamos nos referindo, descrevemos o círculo como uma rosa dos ventos:

Imagem intitulada Memorize o Círculo Unitário Passo 4

4. Lembre-se que a circunferência do círculo é 2π. A circunferência de um círculo é igual a 2πr, através do qual r representa o raio (o raio). Como o círculo unitário tem raio 1, podemos simplificar a circunferência para 2π. O valor radiano de qualquer ponto na circunferência pode ser encontrado simplesmente dividindo 2π pela parte do círculo que você tinha. Isso é muito mais fácil do que memorizar todos os valores do círculo.

Imagem intitulada Memorize o Círculo Unitário Passo 5

5. Indique os quatro pontos nos eixos x e y. Tudo o que você precisa fazer é dividir 2π em quartos:

`Leste` é o ponto de partida, então você tem 0 tinha radianos.

`Norte` = um quarto da circunferência do círculo = /₄ = /₂ radianos.

`Oeste` = metade do círculo = /₂ = π radianos.

`Sul` = três quartos do círculo = 2π * ¾ = /₂ radianos.

Se você caminhar ao longo de todo o perímetro, você retornará ao ponto de partida. Você pode indicar isso como 2π ou 0.

Imagem intitulada Memorize o Círculo Unitário Passo 6

6. Divida o círculo em oito pedaços. Agora desenhe uma linha diagonal através de cada quadrante, perfeitamente através do centro. Novamente, use a divisão para encontrar o valor em radianos:

/₄

(π/2, π, 3π/2 e 2π já foram indicados.)

Imagem intitulada Memorize o Círculo Unitário Passo 7

7. Divida o círculo em seis segmentos. Agora desenhe linhas adicionais que dividem o círculo em seis segmentos. (Você pode usar um transferidor para isso, começando no eixo x positivo, onde cada segmento mede 60 graus). Você pode usar a mesma abordagem acima para garantir que um sexto de um círculo seja igual a /₆ = /₃ radianos. Use este rótulo para os seguintes pontos no perímetro (um em cada quadrante):

/₃

(π e 2π já estão indicados)

Imagem intitulada Memorize o Círculo Unitário Passo 8

8. Desenhe os duodécimos nele. Os últimos pontos marcados na maioria dos círculos unitários indicam incrementos de um duodécimo da circunferência. Apenas quatro deles ainda não foram declarados:

/₆

Parte 2 de 2: Lembre-se das coordenadas x e y (cosseno, seno)

Imagem intitulada Memorize o Círculo Unitário Passo 9

1. Entenda o cosseno e o seno. O círculo unitário é especialmente útil para cálculos trigonométricos com ângulos retos. Qualquer coordenada x de um ponto no círculo é igual a cos(θ) e qualquer coordenada y é igual a sin(θ), onde θ é o valor do ângulo.

Se você achar difícil lembrar, pense em (cos, sin) `porque o seno vem por último`.
Você pode deduzir isso usando triângulos retângulos e a definição dessas funções - lembre-se de `soscastoa`?

Imagem intitulada Memorize o Círculo Unitário Passo 10

2. Anote as coordenadas em quatro pontos do círculo. Um `círculo unitário` é simplesmente um círculo com um raio de exatamente uma unidade. Use-os para encontrar as coordenadas x e y dos quatro pontos no círculo onde ele intercepta um eixo. (Nós os chamamos de `Leste`, `Norte`, etc. para facilitar a leitura, mas estes não são nomes oficiais).

As coordenadas de `Leste` são (1, 0).

As coordenadas de `Norte` são (0, 1).

As coordenadas de `Oeste` são (-1, 0).

As coordenadas de `Sul` são (0, -1).

Isso funciona como um gráfico normal. Você deve ser capaz de encontrar essas coordenadas sozinho, sem ter que memorizá-las.

Imagem intitulada Memorize the Unit Circle Step 11

3. Memorize as coordenadas do primeiro quadrante. O primeiro quadrante é o quarto superior direito do círculo, onde ambos os valores x Enquanto o y-os valores são positivos. Estas são as únicas coordenadas que você precisa lembrar:

Sobre /₆, são as coordenadas ( $\frac{\sqrt{3}}{2}, \frac{1}{2}$ ${frac{{sqrt{3}}}{2}},{frac{1}{2}}$ ).

Sobre /₄, são as coordenadas ( $\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}$ ${frac{{sqrt{2}}}{2}},{frac{{sqrt{2}}}{2}}$ ).

Sobre /₃, são as coordenadas ( $\frac{1}{2}, \frac{\sqrt{3}}{2}$ ${frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ).

Observe que existem apenas três contadores. Você está se movendo em uma direção positiva (da esquerda para a direita para o valores x, de baixo para cima para o valores y), então a sequência é a seguinte: 1 → √2 → √3.

Imagem intitulada Memorize o Círculo Unitário Passo 12

4. Desenhe linhas retas para preencher as outras coordenadas. Se você puder desenhar uma linha perfeitamente vertical ou perfeitamente horizontal entre dois pontos, eles terão o mesmo valor absoluto que as coordenadas x e y. Em outras palavras, você pode desenhar uma linha a partir de um ponto nos primeiros quadrantes, escrever as mesmas coordenadas no ponto em que você pousar e deixar espaço à direita para o sinal (+ ou -).

Por exemplo, você pode desenhar uma linha horizontal entre /₃ e /₃. Como as coordenadas no primeiro ponto (

\frac{1}{2}, \frac{\sqrt{3}}{2}

${frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ), as coordenadas do segundo ponto (?

\frac{1}{2}, ? \frac{\sqrt{3}}{2}

${frac{1}{2}},?{frac{{sqrt{3}}}{2}}$ ), através do qual `?` representa um sinal de mais ou menos (+ ou -).

Aqui está uma maneira mais rápida: verifique o denominador dos radianos. Todos os pontos que terminam em /3 têm as mesmas coordenadas absolutas, assim como todos os pontos que terminam em /4 e todos os pontos que terminam em /6.

Imagem intitulada Memorize o Círculo Unitário Passo 13

5. Use a simetria para descobrir se o sinal é positivo ou negativo. Existem várias maneiras de lembrar onde colocar os sinais de menos no círculo unitário:

Pense em regras fundamentais para gráficos. Acima de X-eixo os pontos são positivos, abaixo dele negativos. À esquerda do y é negativo, o direito é positivo.

Comece do quadrante 1 e desenhe linhas para outros pontos. Se a linha de y-eixo cruza o valor y mudará de sinal. Se a linha de X-eixo cruza, então o valor x muda de sinal.

Aprenda `All Students Test Calculus` (ASTC), no sentido anti-horário. O quadrante 1 tem umaapenas valores positivos, o Quadrante 2 tem apenas valores positivos svalores inus, o Quadrante 3 tem apenas valores positivos tvalores de angens, e o Quadrante 4 tem apenas valores positivos Cvalores de osina.

Independentemente do método escolhido, os sinais são (+, +) para o quadrante 1, (-, +) para o quadrante 2, (-, -) para o quadrante 3 e (+,-) para o quadrante 4.

Imagem intitulada Memorize the Unit Circle Step 14

6. Verifique seu trabalho. Aqui está a lista completa de valores de coordenadas para cada ponto rotulado no círculo (sem contar os quatro pontos nos eixos), no sentido horário. Lembre-se, você deve conseguir encontrar todos esses valores apenas memorizando os pontos do quadrante 1:

Quadrante 1: (

\frac{\sqrt{3}}{2}, \frac{1}{2}

${frac{{sqrt{3}}}{2}},{frac{1}{2}}$ ); (

\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}

${frac{{sqrt{2}}}{2}},{frac{{sqrt{2}}}{2}}$ ); (

\frac{1}{2}, \frac{\sqrt{3}}{2}

${frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ).

Quadrante 2: (

- \frac{1}{2}, \frac{\sqrt{3}}{2}

$-{frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ); (

- \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}

$-{frac{{sqrt{2}}}{2}},{frac{{sqrt{2}}}{2}}$ ); (

- \frac{\sqrt{3}}{2}, \frac{1}{2}

$-{frac{{sqrt{3}}}{2}},{frac{1}{2}}$ )

Quadrante 3: (

- \frac{\sqrt{3}}{2}, - \frac{1}{2}

$-{frac{{sqrt{3}}}{2}},-{frac{1}{2}}$ ); (

- \frac{\sqrt{2}}{2}, - \frac{\sqrt{2}}{2}

$-{frac{{sqrt{2}}}{2}},-{frac{{sqrt{2}}}{2}}$ ); (

- \frac{1}{2}, - \frac{\sqrt{3}}{2}

$-{frac{1}{2}},-{frac{{sqrt{3}}}{2}}$ )

Quadrante 4: (

\frac{1}{2}, - \frac{\sqrt{3}}{2}

${frac{1}{2}},-{frac{{sqrt{3}}}{2}}$ ); (

\frac{\sqrt{2}}{2}, - \frac{\sqrt{2}}{2}

${frac{{sqrt{2}}}{2}},-{frac{{sqrt{2}}}{2}}$ ); (

\frac{\sqrt{3}}{2}, - \frac{1}{2}

${frac{{sqrt{3}}}{2}},-{frac{1}{2}}$ )

Pontas

Se você tiver um teste ou ensaio no círculo unitário, primeiro desenhe o círculo em papel de rascunho para que você possa usá-lo como referência para cada problema.
O processo será consideravelmente mais rápido se você praticar muito. No futuro, talvez você só precise ver os eixos x e y para lembrar de tudo, ou talvez nem precise mais de um gráfico.