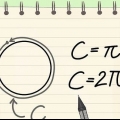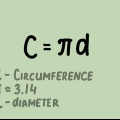Mesmo o botão π em uma calculadora não usa o valor exato de π, embora seja preciso o suficiente. 
C é apenas uma maneira mais curta de escrever `circunferência`. 
Você pode ter escrito o lado esquerdo como π2r, o que também está correto. As pessoas gostam de colocar os números antes dos símbolos para facilitar a leitura da equação, mas isso não altera o resultado da equação. Em uma equação matemática, você sempre pode multiplicar os lados esquerdo e direito pela mesma quantidade e ainda obter uma equação correta. 
Por exemplo, se o raio tem duas unidades de comprimento, então 2πr = 2 x (3,14) x (2 unidades) = 12,56 unidades = a circunferência. No mesmo exemplo, mas usando o botão π de uma calculadora para melhor precisão, você obtém 2 x π x 2 unidades = 12,56637... unidades, mas a menos que instruído de outra forma pelo seu professor, você pode arredondar o número para 12,57 unidades. 

Nós usamos d`, não2º lugar, porque seu problema de matemática lhe diz o que d meios. No entanto, é importante entender esta etapa para que você não fique confuso se seu professor ou livro de matemática 2º lugar usado onde você tem um d esperaria. 
Mesmo o botão π em uma calculadora não usa o valor exato de π, embora seja muito preciso. 

π x d = (C / d) x d πd = C 
Por exemplo, se o diâmetro for seis, você obtém (3,14) x (6) = 18,84. No mesmo exemplo, mas usando o botão π de uma calculadora para maior precisão, você obtém π x 6 = 18,84956... mas, salvo indicação em contrário, você pode arredondar o número para 18,85. 


A = r A / π = πr / π = r √(A/π) = √(r) = r r = √(A/π) 
C = 2πr C = 2π(√(A/π)) 
A resposta para este exemplo é 13,72937... mas, salvo indicação em contrário, você pode arredondar a resposta para 13,73. 


Certifique-se de enrolar a corda em torno dele mais de uma vez. Você deve terminar com um único laço para que não haja parte do círculo onde a corda seja enrolada duas vezes. 

Encontrando a circunferência de um círculo
Contente
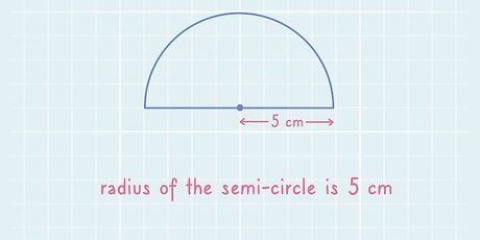
A circunferência de um círculo é a distância em torno de sua borda. Se um círculo tem uma circunferência de 2 milhas, então você tem que andar ao redor do círculo 2 milhas antes de retornar para onde você começou. No entanto, se você está trabalhando em um problema geométrico, não precisa sair da cadeira. Leia o problema cuidadosamente para descobrir se o `raio` (r), `diâmetro` (d) ou `área` (A) do círculo é dado, então encontre a parte deste artigo que se destina a ajudá-lo com a tarefa. Há também instruções para encontrar o perímetro de um objeto circular existente que você deseja medir.
Degraus
Método 1 de 4: Determinando o perímetro usando o raio

1. Desenhe um `raio` no círculo. Desenhe uma linha do centro do círculo para qualquer posição na borda do círculo. Esta linha é o `raio` do círculo, muitas vezes escrito como `r` em equações e fórmulas matemáticas.
- `Observação: se o raio não for fornecido no problema de matemática, essas podem não ser as instruções corretas. Veja se aqueles sobre o diâmetro ou superfície são mais úteis para a atribuição.

2. Desenhe um `diâmetro` sobre o círculo. Estenda a linha que você acabou de desenhar para que ela alcance a borda do círculo do outro lado. Você acabou de desenhar um segundo raio. Os dois raios adicionados têm um comprimento de `2 x o raio`, escrito como 2º lugar. O comprimento desta linha é o `diâmetro` do círculo, muitas vezes escrito como d.

3. Entenda π (`pi`). O símbolo π, também escrito como pi não é um número mágico que é usado nestes tipos de problemas de matemática. Na verdade, o número π foi originalmente `descoberto` medindo círculos: se você medir a circunferência de qualquer círculo (por exemplo, com uma fita métrica) e depois dividir pelo diâmetro, você sempre terá o mesmo número. Este número é incomum porque não pode ser escrito como uma simples fração ou decimal. Em vez disso, podemos arredondar para um número como 3,14, que é "bom o suficiente".

4. Escreva a definição de π como um problema de álgebra. Como explicado acima, π significa apenas `o número que você obtém quando divide a circunferência pelo diâmetro`. Na forma de uma fórmula matemática fica: π = C / d. Como sabemos que o diâmetro é igual a 2 x o raio, também podemos escrever isso como π = C / 2r.

5. Altere este problema para que você resolva este problema para o perímetro C. Queremos saber qual é o perímetro (C neste problema de matemática). Se você multiplicar ambos os lados por 2º lugar você consegue π x 2r = (C / 2r) x 2r, e é o mesmo que 2πr = C.

6. Substituir os números para resolver para C. Agora sabemos que 2πr = C. Retorne ao problema matemático original para ver o que r (o raio) é. Em seguida, substitua π por 3,14 ou use o botão π em sua calculadora para obter uma resposta mais precisa. Calcule 2πr com esses números. A resposta que você obtém é a circunferência.
Método 2 de 4: Determinando a circunferência usando o diâmetro

1. Entenda o que é um `diâmetro`. Coloque o lápis na borda do círculo. Desenhe uma linha no centro do círculo e a borda do outro lado. Esta linha (de borda a borda e através do centro) é o `diâmetro` do círculo, muitas vezes escrito como d em problemas de matemática.
- A linha passa pelo centro exato do círculo, não apenas em qualquer lugar do círculo.
- Observação: Se a instrução não indicar o comprimento do diâmetro, use outro método.

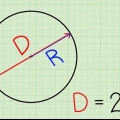
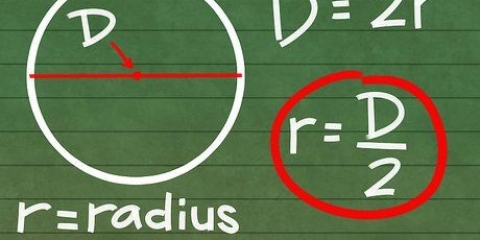
2. Saiba o que significa d = 2r. O `raio` do círculo, também escrito como r, é a distância do centro até a borda do círculo. Como o diâmetro passa pelo círculo de borda a borda, pelo centro, o diâmetro é igual a dois raios. Uma maneira fácil de escrever isso é d = 2r. Isso significa que você d sempre pode substituir por 2º lugar em um problema de matemática e vice-versa.

3. Entenda π (`pi`). O símbolo π, também escrito como pi não é um número mágico que é usado nestes tipos de problemas de matemática. Na verdade, o número π foi originalmente `descoberto` medindo círculos: se você medir a circunferência de qualquer círculo (por exemplo, com uma fita métrica) e depois dividir pelo diâmetro, você sempre terá o mesmo número. Este número é incomum porque não pode ser escrito como uma simples fração ou decimal. Em vez disso, podemos arredondar para um número como 3,14, que é "bom o suficiente".

4. Escreva a definição de π como um problema de álgebra. Como explicado acima, π significa apenas `o número que você obtém quando divide a circunferência pelo diâmetro`. Na forma de uma fórmula matemática é: π = circunferência / diâmetro ou π = C / d.

5. Altere este problema para que você resolva este problema para o perímetro C. Queremos saber qual é o perímetro, então precisamos obter C apenas de um lado. Faça isso multiplicando cada lado da equação por d:

6. Substitua os números e resolva para C. Retorne ao problema original para ver qual é o diâmetro e substitua o d nesta equação por esse número. Substitua π por um arredondamento como 3,14 ou use o botão π em sua calculadora para obter um resultado mais preciso. Multiplique os valores e d juntos e você obtém o perímetro C.
Método 3 de 4: Encontrando o perímetro usando a área

1. Entenda como a área de um círculo é calculada. Normalmente a área (uma) de um círculo não medido diretamente. Em vez disso, você mede o raio (r) do círculo e, em seguida, calcule a área com a fórmula A = r. A razão pela qual esta fórmula faz sentido é um pouco difícil de explicar, mas você pode aprender mais através deste link se você estiver interessado e disposto a chegar ao fundo de alguma álgebra mais pesada.
- Observação: Se o problema de matemática não mencionar a área do círculo, talvez seja necessário usar um método diferente deste artigo.

2. Aprenda uma fórmula para calcular a circunferência. A circunferência (C) é a distância ao redor do círculo. Você geralmente calcula isso com a fórmula C=2πr, mas porque ainda não sabemos qual é o raio (r), teremos que gastar algum tempo descobrindo o valor de r antes de resolvermos a equação.

3. Use a fórmula da área para obter r de um lado. Como A = πr, podemos reorganizar esta fórmula para resolver r em vez. Se você achar os passos abaixo difíceis de seguir, você pode tentar alguns problemas de álgebra mais simples primeiro ou praticar algumas técnicas para entender a álgebra.

4. Altere a fórmula do perímetro usando o que você encontrou. Toda vez que você tem uma equação como r = √(A/π), você pode substituir um lado da equação com o outro?. Vamos usar esta técnica para obter a fórmula da circunferência acima, C=2πr, mudar. Para este problema não sabemos o valor de r, mas sabemos o de A. Vamos alterá-lo assim para tornar o problema solucionável:

5. Substitua os números para encontrar o perímetro. Use a área dada no problema para encontrar o perímetro do perímetro. Por exemplo, se a área (uma) de um círculo é de 15 unidades quadradas, então preencha 2π(√(15/π)) em sua calculadora. Não se esqueça dos colchetes.
Método 4 de 4: Determinando a circunferência de um círculo real

1. Use este método para medir objetos circulares reais. Você pode medir a circunferência dos círculos que encontra no mundo real, não apenas em problemas. Experimente em uma roda de bicicleta, uma pizza ou uma moeda.

2. Pegue um pedaço de barbante e uma régua. A corda deve ser longa o suficiente para envolver o círculo uma vez e flexível o suficiente para caber firmemente. Você precisará de algo para medir a corda mais tarde, como uma régua ou fita métrica. A corda será mais fácil de medir se a régua for maior que o comprimento da corda.

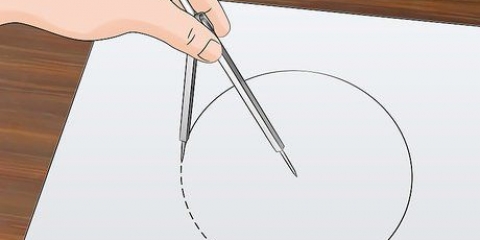
3. Enrole a corda uma vez ao redor do círculo. Comece colocando uma extremidade da corda ao longo da borda do círculo. Enrole a corda ao redor do círculo e puxe-a com força. Se você medir uma moeda ou outro objeto fino, talvez não consiga puxar a corda bem em volta dele. Coloque o objeto circular plano e arrume a corda ao redor dele, o mais apertado possível.

4. Marque ou corte a corda. Encontre o lugar na corda onde o laço termina e toca o final da corda com a qual você começou. Marque este lugar com um marcador, ou corte a corda neste lugar.

5. Solte a corda e meça com uma régua. Pegue a corda enrolada e meça com uma régua. Se você usou um marcador, meça apenas do final da corda até o marcador. Esta é a parte da corda que envolve o círculo e, como a circunferência de um círculo é apenas a distância ao redor do círculo, você encontrou a resposta! O comprimento desta corda é igual à circunferência do círculo.
Pontas
- Você pode escrever o plural de raio como raios ou como raios.
Artigos sobre o tópico "Encontrando a circunferência de um círculo"
Оцените, пожалуйста статью
Popular