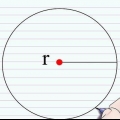
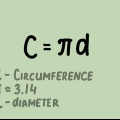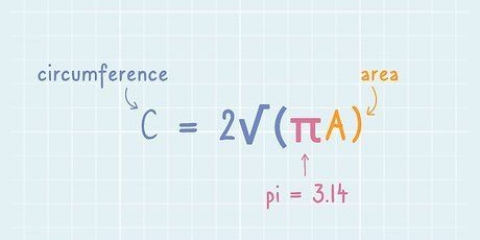O raio (r) de um círculo é a distância de um ponto no círculo ao centro do círculo. O diâmetro (d) de um círculo é a distância de um ponto no círculo a outro ponto diretamente oposto ao círculo, passando pelo centro do círculo. A letra grega pi (π) representa a razão da circunferência dividida pelo diâmetro e é representada pelo número 3,14159265..., um número irracional que não tem um dígito final nem um padrão reconhecível de dígitos repetidos. Esse número geralmente é arredondado para 3,14 para cálculos padrão. 
Na maioria dos problemas de matemática, o raio ou diâmetro é dado. 
Por exemplo: Qual é a circunferência de um círculo com um raio de 3 cm? Escreva a fórmula: C = 2πr Preencha as variáveis: C = 2π3 Multiplicar: C = (2*3*π) = 6π = 18,84 cm Por exemplo: Qual é a circunferência de um círculo com um diâmetro de 9 m? Escreva a fórmula: C = πd Preencha as variáveis: C = 9π Multiplicar: C = (9*π) = 28,26 m 
Determine a circunferência de um círculo com um diâmetro de 5 m. C = πd = 5π = 15,7 m Determine a circunferência de um círculo com um raio de 10 m. C = 2πr = C = 2π10 = 2 *10 *π = 62,8 m. 

O raio (r) de um círculo é a distância de um ponto no círculo ao centro do círculo. O diâmetro (d) de um círculo é a distância de um ponto no círculo a outro ponto diretamente oposto ao círculo, passando pelo centro do círculo. A letra grega pi (π) representa a razão da circunferência dividida pelo diâmetro e é representada pelo número 3,14159265..., um número irracional que não tem um dígito final nem um padrão reconhecível de dígitos repetidos. Esse número geralmente é arredondado para 3,14 para cálculos básicos. 
Na maioria dos problemas de matemática, o raio ou diâmetro é dado. 
Por exemplo: qual é a área de um círculo com um raio de 3 m? Escreva a fórmula: A = r. Preencha as variáveis: A = π3. Quadrado do raio: r = 3 = 9 Multiplique por pi: uma = 9π = 28,26 m Por exemplo: qual é a área de um círculo com um diâmetro de 4 m? Escreva a fórmula: A = π(d/2). Preencha as variáveis: A = π(4/2). Divida o diâmetro por 2: d/2 = 4/2 = 2 Quadrado o resultado: 2 = 4 Multiplique por pi: uma = 4π = 12,56 m 
Encontre a área de um círculo com um diâmetro de 7 m. A = π(d/2) = π(7/2) = π(3,5) = 12,25 * π= 38,47 m. Encontre a área de um círculo com um raio de 3 m. A = πr = π * 3 = 9 * π = 28,26 m 

Por exemplo: calcule a circunferência de um círculo com um raio de (x + 1). Escreva a fórmula: C = 2πr Preencha as informações fornecidas: C = 2π(x+1) 
Por exemplo: calcule a circunferência de um círculo com um raio de (x = 1). C = 2πr = 2π(x+1) = 2πx + 2π1 = 2πx +2π = 6,28x + 6,28 Se o valor de `x` for fornecido posteriormente no problema, você poderá conectá-lo e obter um número inteiro. 
Encontre a área de um círculo com um raio de 2x. A = πr = π(2x) = π4x = 12,56x Encontre a área de um círculo com um diâmetro de (x + 2). A = π(d/2) = π((x +2)/2) = ((x +2)/4)π
Calculando a circunferência e a área de um círculo
Contente
A circunferência (C) de um círculo é sua circunferência, ou a distância ao seu redor. A área (A) de um círculo é quanto espaço o círculo ocupa ou a área delimitada pelo círculo. Tanto a área quanto a circunferência podem ser calculadas com fórmulas simples a partir do raio ou diâmetro do círculo e do valor de pi.
Degraus
Parte 1 de 3: Calculando a circunferência

1. Aprenda a fórmula para a circunferência de um círculo. Existem duas fórmulas que podem ser usadas para calcular a circunferência de um círculo: C = 2πr ou C = d, onde π é a constante matemática e aproximadamente igual a 3,14,r é igual ao raio e d igual ao diâmetro.
- Como o raio de um círculo é igual a duas vezes seu diâmetro, essas equações são essencialmente as mesmas.
- As unidades para a circunferência podem ser qualquer unidade de medida de comprimento: quilômetros, metros, centímetros, etc.

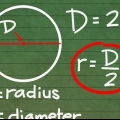
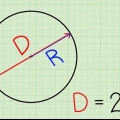
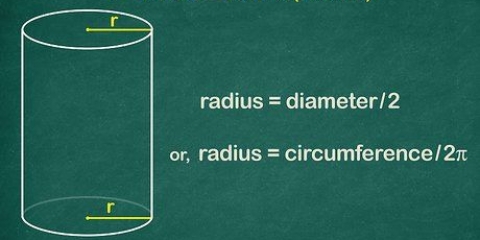
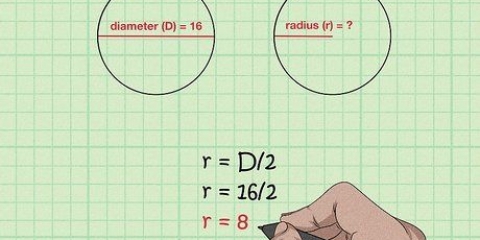
2. Entenda as diferentes partes da fórmula. Existem três componentes para encontrar a circunferência de um círculo: raio, diâmetro e π. O raio e o diâmetro estão relacionados: o raio é igual à metade do diâmetro, enquanto o diâmetro é igual ao dobro do raio.

3. Meça o raio ou diâmetro do círculo. Coloque uma régua em uma borda do círculo, passando pelo centro e para o outro lado do círculo. A distância do centro do círculo é o raio, enquanto a distância da outra extremidade do círculo é o diâmetro.

4. Processe e resolva as variáveis. Depois de determinar o raio e/ou diâmetro do círculo, você pode colocar essas variáveis na equação apropriada. Se você tiver o feixe, use C = 2πr, mas se você souber o diâmetro, use C = d.

5. Pratique com alguns exemplos. Agora que você aprendeu a fórmula, é hora de praticar com alguns exemplos. Quanto mais problemas você resolver, mais fácil será resolvê-los no futuro.
Parte 2 de 3: Calculando a área

1. Aprenda a fórmula para a área de um círculo. A área de um círculo pode ser calculada usando seu diâmetro ou seu raio, com duas fórmulas diferentes: A = r ou A = π(d/2), onde π é a constante matemática aproximadamente igual a 3,14,r o raio e d o diâmetro.
- Como o raio de um círculo é igual à metade de seu diâmetro, essas equações são essencialmente as mesmas.
- As unidades de área podem ser qualquer unidade de comprimento ao quadrado: km ao quadrado (km), metros ao quadrado (m), centímetros ao quadrado (cm), etc.

2. Entenda as diferentes partes da fórmula. Existem três componentes para encontrar a circunferência de um círculo: raio, diâmetro e π. O raio e o diâmetro estão relacionados entre si: o raio é igual à metade do diâmetro, enquanto o diâmetro é igual ao dobro do raio.

3. Meça o raio ou diâmetro do círculo. Coloque uma extremidade de uma régua em um ponto do círculo, passando pelo centro e para o outro lado do círculo. A distância do centro do círculo é o raio, enquanto a distância do outro ponto do círculo é o diâmetro.

4. Preencha as variáveis e resolva-as. Depois de determinar o raio e/ou diâmetro do círculo, você pode inserir essas variáveis na equação apropriada. Se você conhece o raio, use A = r, mas se você souber o diâmetro, use A = π(d/2).

5. Pratique com alguns exemplos. Agora que você aprendeu a fórmula, é hora de praticar com alguns exemplos. Quanto mais problemas você resolver, mais fácil será resolver outros problemas.
Parte 3 de 3: Calculando a área e o perímetro com variáveis

1. Determine o raio ou diâmetro do círculo. Alguns problemas dão um raio ou diâmetro com uma variável, como r = (x + 7) ou d = (x + 3). Neste caso, você ainda pode determinar a área ou o perímetro, mas sua resposta final também conterá essa variável. Anote o raio ou diâmetro conforme indicado na declaração.
- Por exemplo: calcule a circunferência de um círculo com um raio de (x = 1).

2. Escreva a fórmula com as informações fornecidas. Quer você queira calcular área ou perímetro, você ainda segue os passos básicos de preencher o que sabe. Escreva a fórmula para a área ou perímetro e, em seguida, preencha as variáveis fornecidas.

3. Resolva o problema como se a variável fosse um número. Neste ponto, você pode simplesmente resolver o problema como faria normalmente, tratando a variável como se fosse apenas mais um número. Você pode precisar de usando propriedade distributiva para simplificar a resposta final.

4. Pratique com alguns exemplos. Agora que você aprendeu a fórmula, é hora de praticar com alguns exemplos. Quanto mais problemas você resolver, mais fácil será resolver novos.
Artigos sobre o tópico "Calculando a circunferência e a área de um círculo"
Оцените, пожалуйста статью
Popular