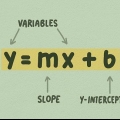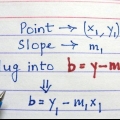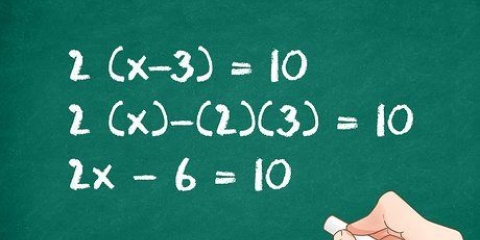Encontre a interseção de uma equação com o eixo Y

Contente

Degraus
Pontas

A interseção y de uma equação é o ponto onde o gráfico de uma equação cruza com o eixo y. Existem várias maneiras de encontrar esta interseção, dependendo das informações fornecidas no início do seu comando.

Degraus

Método 1 de 3: Encontrando a interseção com o eixo y, usando a inclinação

Imagem intitulada Find the Y Intercept Step 1

1. Observe a inclinação. A inclinação de `y sobre x` é um único número que indica a inclinação de uma linha. Este tipo de problema também lhe dá a (x,y)-coordenada de um ponto no gráfico. Se você não tiver esses dois detalhes, continue com os outros métodos abaixo.

Exemplo 1: Uma linha reta com inclinação 2 passa pelo ponto (-3,4). Determine a interseção com o eixo y desta linha usando as etapas abaixo.

Imagem intitulada Find the Y Intercept Step 2

2. Aprenda a forma usual de uma equação linear. Qualquer linha reta pode ser escrita como y = mx + b. Quando a equação está nesta forma, é m a inclinação e a constante b a interseção com o eixo y.

Imagem intitulada Find the Y Intercept Step 3

3. Substitua a inclinação nesta equação. Escreva a equação linear, mas em vez de m você usa a inclinação da sua linha.

Exemplo 1 (continuação):y = mx + b
m = inclinação = 2
y = 2x + b

Imagem intitulada Find the Y Intercept Step 4

4. Substitua x e y pelas coordenadas do ponto. Se você tem as coordenadas de um ponto na linha, você pode X e y-substitui as coordenadas do X e y na sua equação linear. Faça isso para a comparação de sua tarefa.

Exemplo 1 (continuação): O ponto (3,4) está nesta linha. neste ponto, x = 3 e y = 4.
Substitua esses valores em y = 2X +b:
4 = 2(3) + b

Imagem intitulada Find the Y Intercept Step 5

5. Resolva para b. Não esqueça, b é a intersecção com o eixo y da linha. Agora b é a única variável na equação, reorganize a equação para resolver essa variável e encontre a resposta.

Exemplo 1 (continuação):4 = 2(3) + b
4 = 6 + b
4 - 6 = b
-2 = b
A interseção desta linha com o eixo y é -2.

Imagem intitulada Find the Y Intercept Step 6

6. Escreva isso como uma coordenada. A interseção com o eixo y é o ponto onde a linha cruza com o eixo y. Como o eixo y passa pelo ponto x = 0, a coordenada x da interseção com o eixo y é sempre 0.

Exemplo 1 (continuação): A interseção com o eixo y está em y = -2, então o ponto coordenado é (0, -2).

Método 2 de 3: Usando dois pontos

Imagem intitulada Find the Y Intercept Step 7

1. Observe as coordenadas dos dois pontos. Este método lida com problemas em que apenas dois pontos são dados em uma linha reta. Escreva cada coordenada na forma (x,y).

Imagem intitulada Find the Y Intercept Step 8

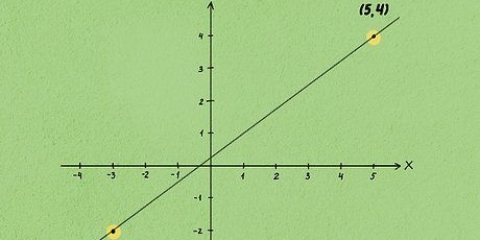
2. Exemplo 2: Uma linha reta passa pelos pontos (1, 2) e (3, -4). Determine a interseção com o eixo y desta linha usando as etapas abaixo.

Imagem intitulada Find the Y Intercept Step 9

3. Calcule os valores de x e y. A inclinação ou inclinação é uma medida de quanto a linha se move na direção vertical para cada passo na direção horizontal. Você pode saber isso como `y sobre x` (

\frac{y}{X}

${frac{y}{x}}$ ). Veja como determinar esses valores usando dois pontos:

A mudança de `y` é a mudança na direção vertical, ou a diferença entre o y-valores dos dois pontos.

A mudança de `x` é a mudança na direção horizontal, ou a diferença entre o X-valores dos dois pontos.

Exemplo 2 (continuação): Os valores de y dos dois pontos são 2 e -4, então a linha aumenta na direção vertical com (-4) - (2) = -6.
Os valores x dos dois pontos (na mesma ordem) são 1 e 3, então a linha aumenta horizontalmente em 3 - 1 = 2.

Imagem intitulada Find the Y Intercept Step 10

4. Divida y por x para determinar a inclinação. Agora que você conhece esses dois valores, você pode usá-los em `

\frac{y}{X}

${frac{y}{x}}$ ` para determinar a inclinação da linha.

Exemplo 2 (continuação):

s eu O p e = \frac{y}{X} = - 6 2 =

$inclinação={frac{y}{x}}={frac{-6}{2}}=$ -3.

Imagem intitulada Find the Y Intercept Step 11

5. Dê outra olhada na forma padrão de uma equação linear. Você pode descrever uma linha reta com a fórmula y = mx + b, através do qual m a inclinação é e b a interseção com o eixo y. Agora que temos a inclinação m e um ponto (x,y), podemos usar esta equação para encontrar b para resolver (a interseção com o eixo y).

Imagem intitulada Find the Y Intercept Step 12

6. Preencha a inclinação e o ponto na equação. Pegue a equação na forma padrão e substitua m pela inclinação que você calculou. Substitua as variáveis X e y pelas coordenadas de um único ponto na linha. Não importa qual ponto você usa.

Exemplo 2 (continuação): y = mx + b
Inclinação = m = -3, então y = -3x + b
A linha passa por um ponto com (x,y)-coordenadas (1,2), então 2 = -3(1) + b.

Imagem intitulada Find the Y Intercept Step 13

7. Resolva para b. Agora a única variável que resta na equação é b, a interseção com o eixo y. Reorganize a equação para que b em um lado da equação, e você tem sua resposta. Lembre-se de que a interseção com o eixo y sempre tem uma coordenada x de 0.

Exemplo 2 (continuação): 2 = -3(1) + b
2 = -3 + b
5 = b
A interseção com o eixo y é (0,5).

Método 3 de 3: Usando uma equação

Imagem intitulada Find the Y Intercept Step 14

1. Escreva a equação da reta. Se você tiver a equação da linha, poderá determinar a interseção com o eixo y com um pouco de álgebra.

Exemplo 3: Qual é a interseção com o eixo y da linha x + 4y = 16?
Nota: O exemplo 3 é uma linha reta. Veja o final desta seção para um exemplo de uma equação quadrática (usando uma variável elevada à potência de 2).

Imagem intitulada Find the Y Intercept Step 15

2. Substituir 0 por x. O eixo y é uma linha vertical passando por x = 0. Isso significa que qualquer ponto no eixo y tem uma coordenada x de 0, incluindo a interseção da linha com o eixo y. Digite 0 para x na equação.

Exemplo 3 (continuação): x + 4y = 16
x = 0
0 + 4a = 16
4a = 16

Imagem intitulada Find the Y Intercept Step 16

3. Resolva para y. A resposta é a interseção da linha com o eixo y.

Exemplo 3 (continuação): 4 anos = 16

4 y 4 = \frac{16}{4}

${frac{4y}{4}}={frac{16}{4}}$
y = 4.
A interseção da linha com o eixo y é 4.

Imagem intitulada Find the Y Intercept Step 17

4. Confirme isso desenhando um gráfico (opcional). Verifique sua resposta fazendo um gráfico da equação com a maior precisão possível. O ponto onde a linha passa pelo eixo y é a interseção com o eixo y.

Imagem intitulada Find the Y Intercept Step 18

5. Encontre a interseção com o eixo y de uma equação quadrática. Uma equação quadrática tem uma variável (x ou y) elevada à segunda potência. Usando a mesma substituição, você pode resolver para y, mas como a equação quadrática é uma curva, ela pode cruzar o eixo y em 0, 1 ou 2 pontos. Isso significa que você terminará com 0, 1 ou 2 respostas.

Exemplo 4: Para encontrar a interseção de

y 2 = X + 1

$y^{2}=x+1$ com o eixo y, você substitui x = 0 e resolva a equação do segundo grau.
Neste caso podemos

y 2 = 0 + 1

$y^{2}=0+1$ resolva tirando a raiz quadrada de ambos os lados. Lembre-se de que você obtém duas respostas ao extrair uma raiz quadrada: uma resposta negativa e uma resposta positiva.

\sqrt{y} 2 = \sqrt{1}

${sqrt{y^{2}}}={sqrt{1}}$
y = 1 ou y = -1. Ambos são interseção com o eixo y desta curva.

Pontas

Alguns países usam um c ou qualquer outra variável para b na equação y = mx + b. Seu significado, no entanto, permanece o mesmo; é apenas uma notação diferente.
Para equações mais complicadas, você pode usar os termos com y isolar em um lado da equação.
Ao calcular a inclinação entre dois pontos, você pode X e y-subtrair coordenadas em qualquer ordem, desde que você coloque o ponto na mesma ordem para y e x. Por exemplo, a inclinação entre (1, 12) e (3, 7) pode ser calculada de duas maneiras diferentes:

Segundo ponto – primeiro ponto: $7 - 12 3 - 1 = - 5 2 = - 2.5$ ${frac{7-12}{3-1}}={frac{-5}{2}}=-2,5$
Primeiro ponto – segundo ponto: $12 - 7 1 - 3 = 5 - 2 = - 2.5$ ${frac{12-7}{1-3}}={frac{5}{-2}}=-2,5$