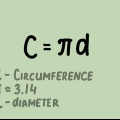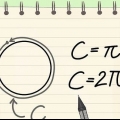Como Calcular o Raio de um Círculo

Contente

Degraus

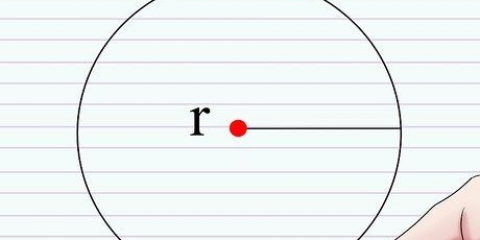
O raio de um círculo é a distância do centro do círculo até a borda. O diâmetro de um círculo é o comprimento da linha reta que pode ser traçada entre dois pontos na esfera ou círculo e através de seu centro.Muitas vezes você é solicitado a calcular o raio de um círculo com base em outros dados. Neste artigo, você aprenderá a calcular o raio de um círculo com base em um determinado diâmetro, circunferência e área. O quarto método é um método mais avançado de determinar o centro e o raio de um círculo com base nas coordenadas de três pontos no círculo.

Degraus

Método 1 de 3: Calcule o raio se você souber o diâmetro

Imagem intitulada Calcule o raio de um círculo Passo 1

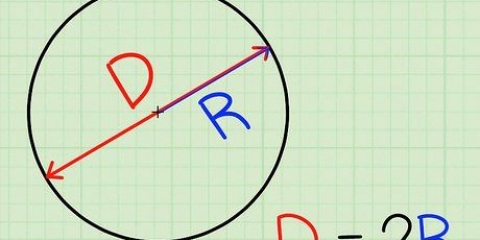
1. Lembre-se de qual é o diâmetro. O diâmetro de um círculo é o comprimento da linha reta que pode ser traçada entre dois pontos na esfera ou círculo e através de seu centro. O diâmetro é a linha mais longa que pode ser traçada através de um círculo e divide o círculo em duas metades. O comprimento do diâmetro também é igual ao comprimento de duas vezes o raio. A fórmula para o diâmetro é a seguinte: D = 2r, onde "d" significa diâmetro e "r" para viga. A fórmula para o raio pode ser derivada da fórmula anterior e é, portanto: r = D/2.

Imagem intitulada Calcule o raio de um círculo Passo 2

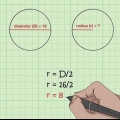
2. Divida o diâmetro por 2 para encontrar o raio. Se você sabe o diâmetro de um círculo, tudo que você precisa fazer é dividi-lo por 2 para encontrar o raio.

Por exemplo, se o diâmetro de um círculo é 4, então a reta é 4/2, ou 2.

Método 2 de 3: Calcule o raio se você souber a circunferência

Imagem intitulada Calcule o raio de um círculo Passo 3

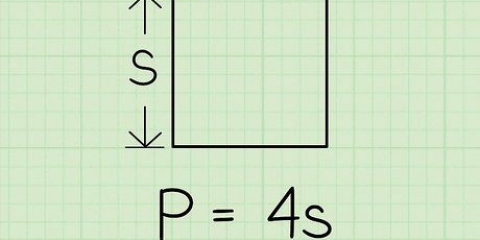
1. Você se lembra da fórmula para a circunferência de um círculo?. A circunferência de um círculo é a distância ao redor do círculo. Outra maneira de olhar para isso é esta: o perímetro é o comprimento da linha que você obtém se você cortar o círculo aberto em um ponto e colocar a linha reta. A fórmula para a circunferência de um círculo é O = 2πr, onde "r" é o raio e π é a constante pi, ou 3,14159... A fórmula para o raio é então r = O/2π.

Normalmente você pode arredondar pi para dois dígitos após o ponto decimal (3,14), mas verifique com seu professor primeiro.

Imagem intitulada Calcule o raio de um círculo Passo 4

2. Calcule o raio com a circunferência dada. Para calcular o raio com base na circunferência, divida a circunferência por 2π, ou 6,28

Por exemplo, se a circunferência é 15, então o raio é r = 15/2π, ou 2,39.

Método 3 de 3: Calcule o raio se você souber as coordenadas de três pontos no círculo

Imagem intitulada Calcule o raio de um círculo Passo 9

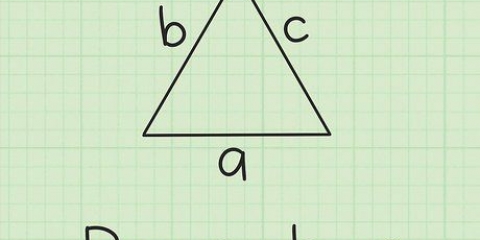
1. Entenda que três pontos podem definir um círculo. Quaisquer três pontos em uma grade definem um círculo tangente aos três pontos. É o círculo circunscrito do triângulo que forma os pontos. O centro do círculo pode cair dentro ou fora do triângulo, dependendo da posição dos três pontos, e ao mesmo tempo é o "interseção" do triângulo.É possível calcular o raio do círculo se você souber as coordenadas xy dos três pontos em questão.

Como exemplo, vamos pegar três pontos definidos da seguinte forma: P1 = (3,4), P2 = (6, 8) e P3 = (-1, 2).

Imagem intitulada Calcule o raio de um círculo Passo 10

2. Use a fórmula da distância para calcular os comprimentos dos três lados do triângulo, que chamamos de a, b e c. A fórmula para a distância entre duas coordenadas (x₁, y₁) e (x₂, y₂) é o seguinte: distância = √(( x₂ - X₁) + (s₂ - y₁)). Agora processe as coordenadas dos três pontos nesta fórmula para encontrar os comprimentos dos três lados do triângulo.

Imagem intitulada Calcule o raio de um círculo Passo 11

3. Calcule o comprimento do primeiro lado a, que vai do ponto P1 ao P2. Em nosso exemplo, as coordenadas de P1 (3,4) e de P2 (6,8), então o comprimento do lado a = √((6 - 3) + (8 - 4)).

a = √(3 + 4)

a = √(9 + 16)

a = √25

a = 5

Imagem intitulada Calcule o raio de um círculo Passo 12

4. Repita o processo para encontrar o comprimento do segundo lado b, que vai de P2 a P3. Em nosso exemplo, as coordenadas de P2 (6,8) e de P3 são (-1,2), então o comprimento do lado b = √((-1 - 6) + (2 - 8)).

b= √(-7 + -6)

b = √(49 + 36)

b = √85

b = 9.23

Imagem intitulada Calcule o raio de um círculo Passo 13

5. Repita o processo para encontrar o comprimento do terceiro lado c, que vai de P3 a P1. No nosso exemplo, as coordenadas de P3 (-1,2) e de P1 (3,4), então o comprimento do lado c =√((3 - -1) + (4 - 2)).

c= √(4 + 2)

c = √(16 + 4)

c = √20

c = 4.47

Imagem intitulada Calcule o raio de um círculo Passo 14

6. Use estes comprimentos na fórmula para encontrar o raio: (abc)/(√(a + b + c)(b + c - a)(c + a - b)(a + b - c)).. O resultado é o raio do nosso círculo!

Os comprimentos do triângulo são os seguintes: a = 5, b = 9.23 ec = 4.47. Então a fórmula para o raio fica assim: r = (5 * 9.23*4.47)/(√(5 + 4.47 + 9.23)(4.47 + 9.23 - 5)(9.23 + 5 - 4.47)(5 + 4.47 - 9.23)).