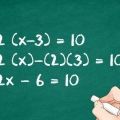Suponha que sabemos que a hipotenusa tem um comprimento de 5 e um dos outros lados tem um comprimento de 3. O comprimento do lado restante é desconhecido. Como dois dos lados são conhecidos, podemos prosseguir para calcular o comprimento do lado desconhecido! Usaremos este exemplo novamente mais tarde. Se o comprimento de dois dos lados são desconhecidos, então você tem que determinar o comprimento de pelo menos mais um lado para poder usar o teorema de Pitágoras. As funções trigonométricas básicas podem ajudá-lo com isso, desde que você conheça um dos outros ângulos não retos do triângulo. 
Em nosso exemplo, conhecemos o comprimento de um lado e o da hipotenusa (3 & 5), então escrevemos nossa equação assim: 3² + b² = 5² 
Em nosso exemplo, elevamos ao quadrado 3 e 5 para obter resp. 9 e 25 para obter. Agora podemos reescrever a equação como 9 + b² = 25. 
Em nosso exemplo, a equação agora é 9 + b² = 25. para B² subtraímos 9 de ambos os lados da equação. Isso nos deixa com b² = 16. 
No nosso exemplo, b² = 16, a equação depois de extrair raízes quadradas é b = 4. Assim, podemos dizer que o comprimento do lado desconhecido do nosso triângulo é igual a 4. 
Vamos dar um exemplo do mundo real. Uma escada se inclina contra uma parede. A base da escada está a 5 metros da parede. A escada chega a 20 metros medidos da parte inferior da parede. Qual o comprimento da escada? "5 metros é a distância até a parede” e "a escada tem 20 metros de altura”. Isso dá uma indicação do comprimento dos lados do triângulo. Como a parede e o chão devem formar um ângulo reto e a escada é diagonal à parede em um ângulo, podemos considerar esse arranjo como um triângulo retângulo, cujos lados têm comprimento a = 5 e b = 20. O comprimento da escada é a hipotenusa, a variável desconhecida c. Vamos aplicar o teorema de Pitágoras aqui: a² + b² = c² (5)² + (20)² = c² 25 + 400 = c² 425 = c² sqrt(425) = c c = 20,6 . O comprimento da escada é (aproximado) 20,6 metros. 


Suponha que temos os pontos (6.1) e (3.5). O comprimento do lado horizontal do nosso triângulo é: |x1 - X2| |3 - 6| | -3 | = 3 O comprimento do lado vertical é: |y1 - y2| |1 - 5| | -4 | = 4 Então podemos dizer que o comprimento dos lados do nosso triângulo retângulo é igual a a = 3 e b = 4. 
Em nosso exemplo, conhecemos os pontos (3,5) e (6.1), e os comprimentos dos lados são a= 3 e b=4, então determinamos a hipotenusa da seguinte forma: sqrt(x) significa "a raiz quadrada de x". Não se esqueça de sempre verificar suas respostas. Se parecer que uma resposta não está certa, verifique seus cálculos ou comece de novo. Se você conhece apenas um lado do triângulo, mas também um dos outros ângulos (do que o ângulo reto), primeiro calcule outro lado usando o que você sabe sobre trigonometria (sen, cos, tan) ou as proporções 30-60-90 / 45-45-90. Outra verificação - o lado mais longo se opõe ao maior ângulo e o lado mais curto se opõe ao menor ângulo.
Usando o teorema de pitágoras
Contente
O teorema de Pitágoras descreve o comprimento dos lados de um triângulo retângulo de uma forma tão elegante e prática que ainda hoje é amplamente utilizado. Isso afirma que para qualquer triângulo retângulo, a soma dos quadrados dos catetos retos é igual ao quadrado da hipotenusa. Em outras palavras, para um triângulo retângulo (um triângulo com lados perpendiculares entre si), com lados de comprimento a e b e uma hipotenusa de comprimento c: a + b = c. O teorema de Pitágoras é um dos pilares da geometria e possui inúmeras aplicações práticas – por exemplo, usando este teorema é muito fácil encontrar a distância entre dois pontos em um plano.
Degraus
Método 1 de 2: O comprimento dos lados de um triângulo retângulo

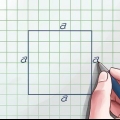
1. Verifique se você está lidando com um triângulo retângulo. O Teorema de Pitágoras só pode ser usado para triângulos retângulos, portanto, antes de prosseguir, é importante estabelecer que seu triângulo atende à definição de triângulo retângulo. Felizmente, há apenas um fator decisivo aqui - um dos cantos do triângulo deve ser um ângulo de 90 graus.
- Uma pista é que os ângulos retos geralmente são marcados com um pequeno colchete para indicar que este é um ângulo de 90 graus. Veja se existe tal colchete em um dos cantos do seu triângulo.

2. Atribua as variáveis a, b e c aos lados do seu triângulo. No teorema de Pitágoras, as variáveis a e b referem-se aos lados retos do triângulo, e a variável c à hipotenusa – o lado maior oposto ao ângulo reto. Então, para começar, você atribui as variáveis a e b (a ordem não importa) aos lados retos e atribui c à hipotenusa.

3. Determine qual lado do triângulo você quer saber. O teorema de Pitágoras permite que você encontre o comprimento de qualquer lado de um triângulo, desde que dois dos lados sejam conhecidos. Determine qual dos lados tem um comprimento desconhecido--uma, b, e/ouc. Se apenas um é desconhecido, então você pode seguir em frente.

4. Calcular usando a equação e os conhecidos. Insira os valores para os comprimentos dos lados do seu triângulo na equação a + b = c. Lembre-se que a e b são os lados retos e c é a hipotenusa.

5. Calcule os quadrados. Para resolver sua equação, comece elevando ao quadrado cada um dos lados conhecidos. Se você achar isso mais fácil, você pode deixar o poder e nivelá-lo mais tarde.

6. Isole a variável desconhecida em um lado do sinal de igual. Opcionalmente, use operações algébricas padrão para obter a incógnita de um lado do sinal de igual e os quadrados do outro lado. Se você está tentando encontrar a hipotenusa, então c já está na posição de um lado, então você pode pular essa etapa.

7. Tire a raiz quadrada de ambos os lados da equação. Agora você deve ter um quadrado (variável) em um lado da equação e um número no outro lado. Agora subtraia a raiz quadrada de ambos os lados para encontrar o comprimento da incógnita.

8. Use o teorema de Pitágoras na prática. A razão pela qual o teorema de Pitágoras é tão usado é porque é aplicável para resolver muitos problemas práticos. Aprenda a reconhecer triângulos retângulos no mundo ao seu redor – sempre que você puder identificar um triângulo retângulo com um ou mais objetos, o teorema de Pitágoras pode ser usado para encontrar o comprimento de um dos lados, desde que haja dois lados ou ângulos famosos.
Método 2 de 2: Calcular a distância entre dois pontos no plano

1. Defina dois pontos no plano. O teorema de Pitágoras pode ser usado muito facilmente para determinar a distância em linha reta entre dois pontos no plano. Tudo que você precisa são as coordenadas x e y de quaisquer dois pontos. Normalmente essas coordenadas são escritas como (x, y).
- Para encontrar a distância entre esses dois pontos, consideramos cada um dos pontos como um dos vértices de um triângulo retângulo, que não pertence ao ângulo reto. Isso torna muito fácil encontrar o comprimento de a e b, após o qual c (a hipotenusa e a distância entre os dois pontos) podem ser calculados.

2. Trace os dois pontos em um gráfico. Em um plano X-Y, para cada ponto (x, y), x é um ponto no eixo x horizontal e y é um ponto no eixo y vertical. Você pode encontrar a distância entre os dois sem representá-los graficamente, mas isso lhe dará uma referência visual para verificar se sua resposta faz sentido.

3. Encontre o comprimento dos lados retos do seu triângulo. Considerando seus dois pontos como os ângulos do triângulo adjacente à hipotenusa, você pode encontrar os comprimentos dos lados a e b. Você pode fazer isso usando o gráfico ou usando as fórmulas |x1 - X2| para o lado horizontal e |y1 - y2| para o lado vertical, onde (x1,y1) é o primeiro ponto e (x2,y2) o segundo ponto.

4. Use o teorema de Pitágoras para encontrar a hipotenusa. A distância entre os dois pontos é o comprimento da hipotenusa do triângulo. Use o teorema de Pitágoras para encontrar a hipotenusa do triângulo, com lados a, b e c.
- (3)²+(4)²= c²
- c= sqrt(9+16)
- c = sqrt(25)
- c = 5. A distância entre (3.5) e (6.1) é 5.
Pontas
- Se o triângulo não é um triângulo retângulo, então você não pode simplesmente usar o teorema de Pitágoras.
- A hipotenusa é sempre:
- a linha oposta ao ângulo reto
- o maior lado do triângulo retângulo
- a variável c no teorema de Pitágoras
Artigos sobre o tópico "Usando o teorema de pitágoras"
Оцените, пожалуйста статью
Popular