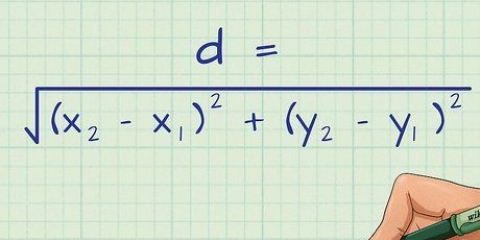Os dois lados mais curtos do triângulo são os lados do quadrado: cada um tem um comprimento s. A hipotenusa é a diagonal do quadrado, d. 


Simplificar: 
Divida os dois lados por dois: 
Área = 
Área = 

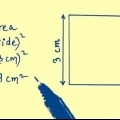
Por exemplo, suponha que um quadrado tenha uma diagonal de 10 cm. Área = 
=
= 50 centímetros. Por exemplo, um quadrado com uma diagonal de 10 cm tem lados de comprimento  cm.
cm. Se você deseja encontrar o comprimento de um lado e a área da diagonal, você pode primeiro usar esta fórmula e depois elevar ao quadrado a resposta para a área: Área  cm. Isso é um pouco menos preciso, porque
cm. Isso é um pouco menos preciso, porque  é um número irracional que pode ter erros de arredondamento.
é um número irracional que pode ter erros de arredondamento. Desenhe um quadrado no papel. Certifique-se de que todos os lados são iguais. Meça a diagonal. Desenhe um segundo quadrado com esse comprimento como os lados do quadrado. Trace uma cópia do seu primeiro quadrado para que você tenha dois. Recorte os três quadrados. Corte os dois quadrados menores em formas que caibam dentro do quadrado grande. Eles devem preencher o espaço perfeitamente, para mostrar que a área do quadrado grande é exatamente o dobro da área do quadrado menor.
Calculando a área de um quadrado usando a diagonal
Contente
A fórmula mais comum para a área de um quadrado é simples: é o comprimento de um de seus lados ao quadrado, ou s. Mas às vezes você só sabe o comprimento da diagonal de um quadrado, a linha entre dois vértices opostos. Se você estiver familiarizado com triângulos retângulos, poderá derivar uma nova fórmula com a diagonal como a única variável.
Degraus
Parte 1 de 2: Calculando a área de um quadrado

1. Desenhe seu quadrado. Um quadrado tem quatro lados iguais. Digamos que cada lado tenha um comprimento de `s`.

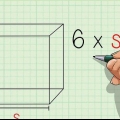
2. Use a fórmula padrão para a área de um quadrado. A área de um quadrado é igual ao seu comprimento vezes a sua largura. Porque cada lado s é se torna fórmula Área = s x s = s. Isso será útil em breve.

3. Conecte dois cantos opostos para fazer uma diagonal. A medida desta diagonal torna-se d unidades. Esta diagonal divide o quadrado em dois triângulos retângulos.

4.Use o teorema de Pitágoras para um dos triângulos. O Teorema de Pitágoras é uma fórmula para encontrar a hipotenusa (lado maior) de um triângulo retângulo: (lado A) + (lado B) = (hipotenusa) ou  . Agora que o quadrado foi dividido ao meio, você pode usar esta fórmula em um dos triângulos retângulos:
. Agora que o quadrado foi dividido ao meio, você pode usar esta fórmula em um dos triângulos retângulos:
 . Agora que o quadrado foi dividido ao meio, você pode usar esta fórmula em um dos triângulos retângulos:
. Agora que o quadrado foi dividido ao meio, você pode usar esta fórmula em um dos triângulos retângulos:

5. Organize a equação de modo que s esteja de um lado. Lembre-se que sabemos que a área do quadrado é s. Se você pode isolar s de um lado, então você tem uma nova equação para a área:






6. Use esta fórmula com um quadrado de exemplo. Esses passos provaram que a fórmula Área =  aplica-se a todos os quadrados. Insira o comprimento da diagonal para d e resolver.
aplica-se a todos os quadrados. Insira o comprimento da diagonal para d e resolver.
 aplica-se a todos os quadrados. Insira o comprimento da diagonal para d e resolver.
aplica-se a todos os quadrados. Insira o comprimento da diagonal para d e resolver.
=

= 50 centímetros.
Parte 2 de 2: Informações adicionais
1. Encontre a diagonal do comprimento de um lado. O teorema de Pitágoras para um quadrado com lado s e diagonal d dar-lhe a fórmula  sobre. Resolva para `d` se você conhece os comprimentos dos lados e deseja determinar o comprimento da diagonal:
sobre. Resolva para `d` se você conhece os comprimentos dos lados e deseja determinar o comprimento da diagonal:
 sobre. Resolva para `d` se você conhece os comprimentos dos lados e deseja determinar o comprimento da diagonal:
sobre. Resolva para `d` se você conhece os comprimentos dos lados e deseja determinar o comprimento da diagonal: - Por exemplo, se um quadrado tem lados de 7 cm, então a diagonal é d = 7√2 cm, ou cerca de 9,9 cm.
- Se você não tiver uma calculadora, você pode usar 1,4 como uma estimativa de √2.
2. Determine o comprimento de um lado usando a diagonal. A diagonal é dada e você sabe que a diagonal de um quadrado  então você pode dividir ambos os lados por
então você pode dividir ambos os lados por  para
para  para obter.
para obter.
 então você pode dividir ambos os lados por
então você pode dividir ambos os lados por  para
para  para obter.
para obter. cm.
cm. cm. Isso é um pouco menos preciso, porque
cm. Isso é um pouco menos preciso, porque  é um número irracional que pode ter erros de arredondamento.
é um número irracional que pode ter erros de arredondamento.3. Interprete a fórmula da superfície. A fórmula Área =  parece ser matematicamente correto, mas existe uma maneira de testar isso diretamente? Nós vamos,
parece ser matematicamente correto, mas existe uma maneira de testar isso diretamente? Nós vamos,  é a área de um segundo quadrado com a diagonal como lado. Porque a fórmula completa
é a área de um segundo quadrado com a diagonal como lado. Porque a fórmula completa  você pode raciocinar que este segundo quadrado tem exatamente o dobro da área do quadrado original. Você mesmo pode testar isso:
você pode raciocinar que este segundo quadrado tem exatamente o dobro da área do quadrado original. Você mesmo pode testar isso:
 parece ser matematicamente correto, mas existe uma maneira de testar isso diretamente? Nós vamos,
parece ser matematicamente correto, mas existe uma maneira de testar isso diretamente? Nós vamos,  é a área de um segundo quadrado com a diagonal como lado. Porque a fórmula completa
é a área de um segundo quadrado com a diagonal como lado. Porque a fórmula completa  você pode raciocinar que este segundo quadrado tem exatamente o dobro da área do quadrado original. Você mesmo pode testar isso:
você pode raciocinar que este segundo quadrado tem exatamente o dobro da área do quadrado original. Você mesmo pode testar isso:Pontas
- Esta equação simples é usada em muitos campos, incluindo cristalografia, química e arte. Por exemplo, você pode usá-lo para calcular a área de uma paisagem que você vê durante o levantamento, ou ao usar perspectiva em fotografia ou pintura, medindo a distância que você andou e imaginando uma grade dessa distância como diagonal.
- Se você quer ter uma abordagem mais visual da matemática, ou aprender a usar gráficos e tabelas na arte, ou explorar o caminho espiral de uma partícula, confira alguns artigos sobre Microsoft Excel, matemática, planilhas e gráficos.
- Se você não tem uma calculadora, mas precisa de uma estimativa mais precisa da raiz quadrada de dois, existem maneiras de para fazer isso à mão. Um exemplo disso é o método de Newton-Raphson.
Artigos sobre o tópico "Calculando a área de um quadrado usando a diagonal"
Оцените, пожалуйста статью
Similar
Popular