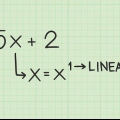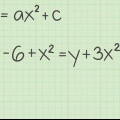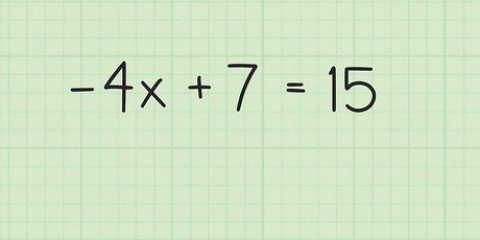Usando a propriedade distributiva para resolver uma equação

Contente

Degraus
Pontas

A propriedade distributiva é uma regra em matemática para simplificar uma equação com parênteses. Você provavelmente aprendeu desde cedo que precisa fazer as operações entre parênteses primeiro, mas com expressões algébricas, isso nem sempre é possível. A propriedade distributiva permite que você multiplique o termo fora dos parênteses pelos termos dentro dele. Você tem que ter cuidado para fazer da maneira certa, caso contrário você pode perder informações e a comparação não está mais correta. Você também pode usar a propriedade distributiva para simplificar equações com frações.

Degraus

Método 1 de 4: Usando a Propriedade Distributiva Fundamental

Imagem intitulada Use a propriedade distributiva para resolver uma equação Etapa 1

1. Multiplique o termo fora dos parênteses por qualquer termo dentro dos parênteses. Para fazer isso, você basicamente divide o termo externo entre os termos internos. Multiplique o termo fora dos parênteses pelo primeiro termo dentro dos parênteses. Então você multiplica pelo segundo termo. Se houver mais de dois termos, continue a distribuir o termo fora dos parênteses em todos os termos dentro dos parênteses. Basta deixar os operadores (mais ou menos) dentro dos parênteses.

$2 (X - 3) = 10$ $2(x-3)=10$
$2 (X) - (2) (3) = 10$ $2(x)-(2)(3)=10$
$2 X - 6 = 10$ $2x-6=10$

Imagem intitulada Use a propriedade distributiva para resolver uma equação Etapa 2

2. Combinar termos semelhantes. Antes de resolver a equação, você deve combinar termos semelhantes. Combine todos os termos numéricos entre si. Além disso, você combina todos os termos variáveis separadamente. Para simplificar a equação, ordene os termos de forma que as variáveis fiquem de um lado do sinal de igual e as constantes (apenas os números) do outro lado.

2 X - 6 = 10

$2x-6=10$ ....(problema original)

2 X - 6 (+ 6) = 10 (+ 6)

$2x-6(+6)=10(+6)$ .... (adicione 6 em ambos os lados)

2 X = 16

$2x=16$ .... (Variável à esquerda; constante à direita)

Imagem intitulada Use a propriedade distributiva para resolver uma equação Etapa 3

3. Resolva a equação. solto

X

$X$ dividindo ambos os lados da equação pelo coeficiente da variável.

2 X = 16

$2x=16$ ....(problema original)

2 X / 2 = 16 / 2

$2x/2=16/2$ ....(dividir ambos os lados por 2)

X = 8

$x=8$ ....(solução)

Método 2 de 4: Distribuir coeficientes negativos

Imagem intitulada Use a propriedade distributiva para resolver uma equação Etapa 4

1. Distribuir um número negativo junto com o sinal de menos. Se você for multiplicar um termo ou termos entre parênteses por um número negativo, certifique-se de aplicar o sinal de menos a cada termo dentro dos parênteses.

Lembre-se das regras básicas para multiplicar por números negativos:

Menos x Menos = Mais.
Menos x Mais = Menos.

Observe o seguinte exemplo:

- 4 (9 - 3 X) = 48

$-4(9-3x)=48$ .... (problema original)

- 4 (9) - (- 4) (3 X) = 48

$-4(9)-(-4)(3x)=48$ ....(multiplique -4 por cada termo)

- 36 - (- 12 X) = 48

$-36-(-12x)=48$ ....(simplifique a multiplicação)

- 36 + 12 X = 48

$-36+12x=48$ ....(note que `menos -12` é o mesmo que +12)

Imagem intitulada Use a propriedade distributiva para resolver uma equação Etapa 5

2. Combinar termos semelhantes. Depois de concluir a distribuição, você precisa simplificar a equação, movendo todos os termos variáveis para um lado do sinal de igual e todos os números sem variáveis para o outro lado. Você faz isso por meio de uma combinação de adição ou subtração.

- 36 + 12 X = 48

$-36+12x=48$ ....(problema original)

- 36 (+ 36) + 12 X = 48 + 36

$-36(+36)+12x=48+36$ ....(adicione 36 para cada lado)

12 X = 84

$12x=84$ ....(simplifique a adição para isolar a variável)

Imagem intitulada Use a propriedade distributiva para resolver uma equação Etapa 6

3. Compartilhe para obter a solução final. Resolva a equação dividindo ambos os lados da equação pelo coeficiente da variável. Isso deve resultar em uma única variável em um lado da equação, com o resultado no outro lado.

12 X = 84

$12x=84$ ....(problema original)

12 X / 12 = 84 / 12

$12x/12=84/12$ ....(dividir ambos os lados por 12)

X = 7

$x=7$ ....(solução)

Imagem intitulada Use a propriedade distributiva para resolver uma equação Etapa 7

4. Trate a subtração como adição (de -1). Quando você vê um sinal de menos em um problema de álgebra, especialmente se estiver antes de um parêntese, ele essencialmente diz + (-1). Isso ajuda a distribuir corretamente o sinal de menos em todos os termos entre parênteses. Então resolva o problema como antes.

Por exemplo, considere o problema,

4 X - (X + 2) = 4

$4x-(x+2)=4$ . Para garantir que você distribuiu corretamente o sinal de menos, reescreva o problema assim:

4 X + (- 1) (X + 2) = 4

$4x+(-1)(x+2)=4$

Então você distribui -1 pelos termos entre parênteses, como segue:

4 X + (- 1) (X + 2) = 4

$4x+(-1)(x+2)=4$ ....(edição modificada)

4 X - X - 2 = 4

$4x-x-2=4$ ....(multiplique -1 por x e por 2)

3 X - 2 = 4

$3x-2=4$ ....(combinar termos)

3 X - 2 + 2 = 4 + 2

$3x-2+2=4+2$ ....(adicione 2 em ambos os lados)

3 X = 6

$3x=6$ ....(simplifique os termos)

3 X / 3 = 6 / 3

$3x/3=6/3$ ....(dividir ambos os lados por 3)

X = 2

$x=2$ ....(solução)

Método 3 de 4: Use a propriedade distributiva para simplificar frações

Imagem intitulada Use a propriedade distributiva para resolver uma equação Etapa 8

1. Descubra se existem coeficientes fracionários ou constantes. Às vezes você pode precisar resolver um problema com frações como coeficientes ou constantes. Você pode deixá-los como estão e aplicar as regras fundamentais da álgebra a eles, para resolver o problema. No entanto, usando a propriedade distributiva, muitas vezes você pode simplificar a solução convertendo as frações em inteiros.

Confira o exemplo a seguir $X - 3 = \frac{X}{3} + \frac{1}{6}$ $x-3={frac{x}{3}}+{frac{1}{6}}$ . As frações neste exemplo são $\frac{X}{3}$ ${frac{x}{3}}$ e $\frac{1}{6}$ ${frac{1}{6}}$ .

Imagem intitulada Use a propriedade distributiva para resolver uma equação Etapa 9

2. Encontre o Mínimo Múltiplo Comum (MLC) para todos os denominadores. Nesta etapa você pode ignorar todos os números inteiros. Basta olhar para as frações e determinar o LCF para todos os denominadores. Determine o kgf procurando o menor número que é um múltiplo dos denominadores de ambas as frações na equação. Neste exemplo, os denominadores são 3 e 6, então 6 é o kgf.

Imagem intitulada Use a propriedade distributiva para resolver uma equação Etapa 10

3. Multiplique todos os termos da equação pelo kgf. Lembre-se, você pode aplicar qualquer operação a uma equação matemática, desde que a faça em ambos os lados. Multiplicando cada termo da equação pelo lcg, os termos se cancelam e `tornam-se` inteiros. Coloque seus parênteses ao redor de todos os lados esquerdo e direito da equação, então faça a distribuição:

X - 3 = \frac{X}{3} + \frac{1}{6}

$x-3={frac{x}{3}}+{frac{1}{6}}$ ....(equação original)

(X - 3) = (\frac{X}{3} + \frac{1}{6})

$(x-3)=({frac{x}{3}}+{frac{1}{6}})$ ....(aplicar parênteses)

6 (X - 3) = 6 (\frac{X}{3} + \frac{1}{6})

$6(x-3)=6({frac{x}{3}}+{frac{1}{6}})$ ....(multiplique ambos os lados pelo kgf)

6 X - 6 (3) = 6 (\frac{X}{3}) + 6 (\frac{1}{6})

$6x-6(3)=6({frac{x}{3}})+6({frac{1}{6}})$ ....(distribuir a multiplicação)

6 X - 18 = 2 X + 1

$6x-18=2x+1$ ....(simplifique a multiplicação)

Imagem intitulada Use a propriedade distributiva para resolver uma equação Etapa 11

4. Combinar termos semelhantes. Combine todos os termos de modo que todas as variáveis fiquem de um lado da equação e todas as constantes do outro lado. Use as operações básicas de adição e subtração para mover termos de um lado da equação para o outro.

6 X - 18 = 2 X + 1

$6x-18=2x+1$ ....(problema simplificado)

6 X - 2 X - 18 = 2 X - 2 X + 1

$6x-2x-18=2x-2x+1$ ....(subtrair 2x de ambos os lados)

4 X - 18 = 1

$4x-18=1$ ....(simplifique menos a soma)

4 X - 18 + 18 = 1 + 18

$4x-18+18=1+18$ ....(adicione 18 em ambos os lados)

4 X = 19

$4x=19$ ....(simplifique a adição)

Imagem intitulada Use a propriedade distributiva para resolver uma equação Etapa 12

5. Resolva a equação. Encontre a solução final dividindo ambos os lados da equação pelo coeficiente da variável. Isso deixa você com x de um lado da equação e a solução numérica do outro.

4 X = 19

$4x=19$ ....(questão personalizada)

4 X / 4 = 19 / 4

$4x/4=19/4$ ....(dividir ambos os lados por 4)

X = \frac{19}{4} ou 4 \frac{3}{4}

$x={frac{19}{4}}{text{ ou }}4{frac{3}{4}}$ ....(solução final)

Método 4 de 4: Distribuir uma fração com uma equação

Imagem intitulada Use a propriedade distributiva para resolver uma equação Etapa 13

1. Interpretar uma fração com uma equação como uma divisão distribuída. Às vezes você vê um problema com vários termos no numerador de uma fração, acima de um denominador comum. Você tem que tratar isso como um problema distributivo e aplicar o denominador a cada termo do numerador. Você pode reescrever a fração para mostrar a distribuição. Do seguinte modo:

$4 X + 8 2 = 4$ ${frac{4x+8}{2}}=4$ .....(problema original)
$4 X 2 + \frac{8}{2} = 4$ ${frac{4x}{2}}+{frac{8}{2}}=4$ .....(multiplique o denominador por cada termo do numerador)

Imagem intitulada Use a propriedade distributiva para resolver uma equação Etapa 14

2. Simplifique cada numerador como fração separada. Depois de distribuir o divisor em cada termo, você pode simplificar cada termo individualmente.

4 X 2 + \frac{8}{2} = 4

${frac{4x}{2}}+{frac{8}{2}}=4$ .....(questão personalizada)

2 X + 4 = 4

$2x+4=4$ .....(simplifique as frações)

Imagem intitulada Use a propriedade distributiva para resolver uma equação Etapa 15

3. Isolar a variável. Continue resolvendo o problema isolando a variável em um lado da equação e movendo os termos constantes para o outro lado. Faça isso através de uma combinação de adição e subtração, quando necessário.

2 X + 4 = 4

$2x+4=4$ .....(questão personalizada)

2 X + 4 - 4 = 4 - 4

$2x+4-4=4-4$ .....(subtrair 4 de ambos os lados)

2 X = 0

$2x=0$ .....(isolar x de um lado)

Imagem intitulada Use a propriedade distributiva para resolver uma equação Etapa 16

4. Divida pelo coeficiente para resolver o problema. Na última etapa você divide pelo coeficiente da variável. Isso dá a solução final, com a única variável de um lado da equação e a solução numérica do outro.

2 X = 0

$2x=0$ .....(questão personalizada)

2 X / 2 = 0 / 2

$2x/2=0/2$ .....(dividir ambos os lados por 2)

X = 0

$x=0$ .....(solução)

Imagem intitulada Use a propriedade distributiva para resolver uma equação Etapa 17

5. Evite o erro comum de compartilhar apenas um termo. É tentador (mas incorreto) dividir o primeiro termo do numerador pelo denominador e eliminar a fração. Um erro como este ficaria assim para o problema acima:

4 X + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(problema original)

2 X + 8 = 4

$2x+8=4$ .....(apenas 4x é dividido por 2, em vez do contador completo)

2 X + 8 - 8 = 4 - 8

$2x+8-8=4-8$

2 X = - 4

$2x=-4$

X = - 2

$x=-2$ ..... (solução errada)

Imagem intitulada Use a propriedade distributiva para resolver uma equação Etapa 18

6. Verifique a correção da sua solução. Você sempre pode verificar seu trabalho inserindo sua solução no problema original. Quando você quer simplificar, você tem que chegar a uma afirmação verdadeira. Se você simplificar e receber uma afirmação incorreta como resposta, sua solução está incorreta. Neste exemplo, você testa as duas soluções para x = 0 e x =-2 para ver qual está correta.

Comece com a solução x=0:

4 X + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(problema original)

4 (0) + 8 2 = 4

${frac{4(0)+8}{2}}=4$ .....(substitua 0 por x)

0 + 8 2 = 4

${frac{0+8}{2}}=4$

\frac{8}{2} = 4

${frac{8}{2}}=4$

4 = 4

$4=4$ .....(Verdadeiro. Esta é a solução certa.)

Tente a `solução errada para x=-2:

4 X + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(problema original)

4 (- 2) + 8 2 = 4

${frac{4(-2)+8}{2}}=4$ .....(insira -2 para x)

- 8 + 8 2 = 4

${frac{-8+8}{2}}=4$

\frac{0}{2} = 4

${frac{0}{2}}=4$

0 = 4

$0=4$ .....(Declaração incorreta. Portanto x=-2 é falso.)

Pontas

Você também pode usar a propriedade distributiva para simplificar algumas multiplicações. Você pode dividir os números em dezenas com um resto para tornar a aritmética mental mais fácil. Por exemplo, você pode reescrever 8 x 16 como 8(10+6). Este é então simplesmente 80 + 48 = 128. Outro exemplo, 7 x 24 = 7(20 + 4) = 7(20) + 7(4) = 140 + 28 = 168. Pratique-os de cor e a aritmética mental se tornará muito mais fácil.