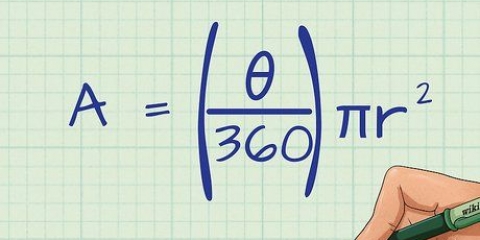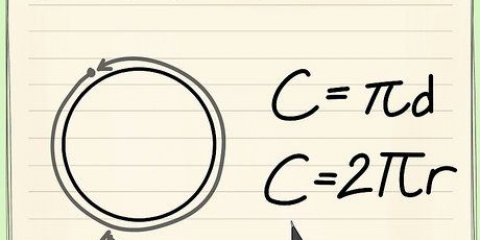Calculando a circunferência por área: 10 passos (com imagens)

Contente

Degraus
- Método 1 de 2: Usando a equação do perímetro
- Método 2 de 2: Corrija o problema ao contrário

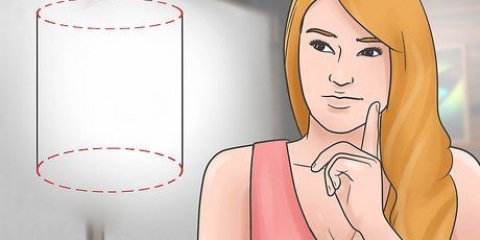
A fórmula para calcular a circunferência (C) de um círculo, C = πD ou C = 2πR, é simples se você souber o diâmetro do círculo (D) ou o raio (R). Mas o que você faz se você conhece apenas a área do círculo? Como muitas coisas em matemática, existem várias soluções para este problema. A fórmula C = 2√πA é projetada para encontrar a circunferência de um círculo usando a área (A). Você também pode reverter a equação A = πR para encontrar R e inserir R na equação do perímetro. Ambas as equações dão o mesmo resultado.

Degraus

Método 1 de 2: Usando a equação do perímetro

Imagem intitulada Encontre a circunferência de um círculo usando sua área Passo 1

1. Use a fórmula C=2√πA para resolver o problema. Esta fórmula calcula a circunferência de um círculo se você conhece apenas sua área. C representa o perímetro e A a área. Escreva esta fórmula para começar a resolver o problema.

O símbolo π, que significa pi, é uma dízima periódica com (agora) milhares de dígitos após o ponto decimal. Para simplificar, use 3,14 como o valor de pi.
Como você precisa converter pi para sua forma numérica de qualquer maneira, use 3,14 na equação desde o início. Escreva como C = 2√3,14 x A.

Imagem intitulada Encontre a circunferência de um círculo usando sua área Passo 2

2. Inclua a área como A na equação. Como você já conhece a área do círculo, esse é o valor de A. Em seguida, prossiga para resolver o problema usando a ordem das operações.

Digamos que a área do círculo seja 500 cm. Então você resolve a equação da seguinte forma: 2√3,14 x 500.

Imagem intitulada Encontre a circunferência de um círculo usando sua área Passo 3

3. Multiplique pi pela área do círculo. Na ordem das operações, as operações dentro do símbolo de raiz quadrada vêm primeiro. Multiplique pi pela área do círculo que você conectou. Em seguida, insira esse resultado na equação.

Se o cálculo for igual a 2√3,14 x 500, então você primeiro calcula 3,14 x 500 = 1570. Então calcule 2√1.570.

Imagem intitulada Encontre a circunferência de um círculo usando sua área Passo 4

4. Especialraiz quadrada da soma. Existem várias maneiras de calcular a raiz quadrada. Se estiver usando uma calculadora, pressione a função √ e digite o número. Você também pode resolver o problema manualmente usando fatores primos.

A raiz quadrada de 1570 é 39,6.

Imagem intitulada Encontre a circunferência de um círculo usando sua área Passo 5

5. Multiplique a raiz quadrada por 2 para encontrar o perímetro. Finalmente, você completa o cálculo multiplicando o resultado por 2. Isso retorna um número final, a circunferência.

Calcular 39,6 x 2 = 79,2. Isso significa que a circunferência é 79,2 cm, o que resolve a fórmula.

Método 2 de 2: Corrija o problema ao contrário

Imagem intitulada Encontre a circunferência de um círculo usando sua área Passo 6

1. Use a fórmula A = πR em. Esta é a fórmula para a área de um círculo. A representa a área e R o raio. Normalmente você usaria se soubesse o raio, mas também pode preencher a área para resolver a equação.

Novamente, use 3,14 como o valor arredondado para pi.

Imagem intitulada Encontre a circunferência de um círculo usando sua área Passo 7

2. Insira a área como valor para A. Use a área do círculo na equação. Coloque isso à esquerda da equação como o valor para A.

Suponha que a área do círculo seja 200 cm. A equação então se torna 200 = 3,14 x R.

Imagem intitulada Encontre a circunferência de um círculo usando sua área Passo 8

3. Divida ambos os lados da equação por 3,14. Para resolver esse tipo de equação, você deve eliminar gradualmente os passos da direita fazendo as operações opostas. Como você sabe o valor de pi, você divide cada lado por esse valor. Isso elimina pi à direita e fornece um novo valor numérico à esquerda.

Se você dividir 200 por 3,14, o resultado será 63,7. Então a nova equação é 63,7 = R.

Imagem intitulada Encontre a circunferência de um círculo usando sua área Passo 9

4. Especialraiz quadrada do resultado para obter o raio do círculo. Então o expoente do lado direito da equação é eliminado. O oposto de `exponenciação` é encontrar a raiz quadrada do número. Encontre a raiz quadrada de cada lado da equação. Isso remove o expoente à direita e coloca o raio à esquerda.

A raiz quadrada de 63,7 é 7,9. A equação então se torna 7,9 = R, o que significa que o raio do círculo é 7,9. Isso lhe dará todas as informações necessárias para encontrar o perímetro.

Imagem intitulada Encontre a circunferência de um círculo usando sua área Passo 10

5.Determine a circunferência do círculo usando o raio. Existem duas fórmulas para encontrar o perímetro (C). A primeira é C = πD, onde D é o diâmetro. Multiplique o raio por 2 para encontrar o diâmetro. A segunda é C = 2πR. Multiplique 3,14 por 2 e depois multiplique o resultado pelo raio. Ambas as fórmulas lhe darão o mesmo resultado.

Use a primeira opção, 7,9 x 2 = 15,8, o diâmetro do círculo. Este diâmetro vezes 3,14 é 49,6.

Para a segunda opção, o cálculo passa a ser 2 x 3,14 x 7,9. Primeiro você calcula 2 x 3,14 = 6,28, e isso multiplicado por 7,9 é 49,6. Observe como os dois métodos fornecem a mesma resposta.