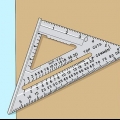
Usando a Regra 3 4 5 para Determinar Ângulos Retos: 4 Passos (com Imagens)

Contente

Degraus
- Método 1 de 1: usando a regra 3-4-5
Pontas
Necessidades

Um dos desafios de fazer cantos é deixá-los quadrados. É claro que sua sala não precisa ter ângulos perfeitamente retos, mas é sempre útil se aproximar de 90 graus o mais próximo possível. Caso contrário, você verá que as paredes não estão completamente niveladas com carpete ou azulejos. O método 3-4-5 também é útil para pequenos projetos de marcenaria, para garantir que todas as peças se encaixem exatamente como planejado.

Degraus

Método 1 de 1: usando a regra 3-4-5

Imagem intitulada Use a regra 3 4 5 para construir cantos quadrados Passo 1

1. Entenda o método 3-4-5. Se um triângulo tem lados de 3, 4 e 5 metros respectivamente (ou qualquer outra unidade), então estamos lidando com um triângulo retângulo com um ângulo de 90º entre os lados curtos. Se você pode `encontrar` este triângulo no seu canto, então você sabe com certeza que o canto é quadrado. Isso é baseado em o teorema de Pitágoras , você pode se lembrar da matemática: A + B = C em um triângulo retângulo. C é o lado mais longo (hipotenusa) e A e B são os dois lados mais curtos.

3-4-5 é uma medida fácil de verificar porque os números são pequenos e porque são números inteiros. A fórmula está absolutamente correta: 3 + 4=9 + 16=25=5.

Imagem intitulada Use a regra 3 4 5 para construir cantos quadrados Passo 2

2. Meça três unidades do canto ao longo de um lado. Isso pode ser metros ou centímetros, ou outras unidades. Coloque uma marca no final de três unidades.

Você pode multiplicar qualquer número pelo mesmo número e ainda funcionará. Por exemplo, você também pode usar 30-40-50 centímetros ou, no caso de uma sala grande, 6-8-10 ou 9-12-15 metros.

Imagem intitulada Use a regra 3 4 5 para construir cantos quadrados Passo 3

3. Meça quatro unidades do canto ao longo do outro lado. Usando a mesma unidade, meça (espero) em um ângulo de 90 ao longo do outro lado. Marque o ponto no final das quatro unidades.

Imagem intitulada Use a regra 3 4 5 para construir cantos quadrados Passo 4

4. Mede a distância entre as marcas. Se a distância for 5 unidades você tem um ângulo reto.

Se a distância for menor que 5 unidades, então o ângulo é menor que 90º. Em seguida, afaste ligeiramente os lados.

Se a distância for superior a 5 unidades, então o ângulo é superior a 90º. Em seguida, mova os lados um para o outro.

Pontas

Este método pode fornecer resultados mais precisos do que um quadrado quadrado, porque geralmente são muito pequenos para fazer medições precisas em uma escala maior.
Quanto maior a unidade, mais preciso o resultado.