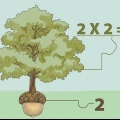
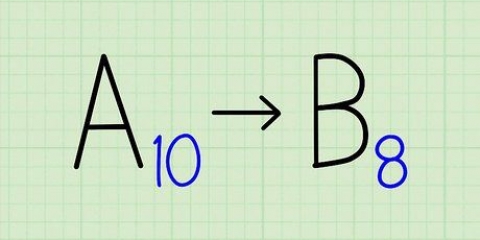No nosso exemplo tiramos as raízes quadradas de 25 e 16. Ver abaixo: Quadrado(25×16) Quadrado(25) × Quadrado(16) 5 × 4 = 20 
Vamos pegar a raiz quadrada de 147 como exemplo. 147 não é o produto de dois quadrados perfeitos, então não podemos obter um bom valor inteiro. Mas é o produto de um quadrado perfeito e outro número - 49 e 3. Podemos usar essas informações para escrever nossa resposta nos termos mais simples: sqrt(147) = Quadrado(49 × 3) = Quadrado(49) × Quadrado(3) = 7 × Quadrado(3) 
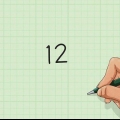
Vamos voltar ao nosso exemplo. Como 2 = 4 e 1 = 1, sabemos que Sqrt(3) está entre 1 e 2 – provavelmente mais próximo de 2 do que 1. Estimamos que 1,7. 7 × 1,7 = 11,9. Verificando isso com a calculadora, vemos que estamos bem próximos da resposta: 12.13. Isso também funciona para os números maiores. Por exemplo, Sqrt(35) está aproximadamente entre 5 e 6 (provavelmente mais próximo de 6). 5 = 25 e 6 = 36. 35 está entre 25 e 36, então a raiz quadrada estará entre 5 e 6. Como 35 está logo abaixo de 36, podemos dizer com alguma confiança que sua raiz quadrada somente é inferior a 6. Verificando com uma calculadora nos dá uma resposta de cerca de 5,92 - estávamos certos. 
Um exemplo: determinamos a raiz quadrada de 45 usando este método. Sabemos que 45 = 9 × 5 e que 9 = 3 × 3. Então podemos escrever a raiz quadrada assim: Sqrt(3 × 3 × 5). Basta remover os 3 e colocar um 3 fora do radical para obter uma raiz quadrada simplificada: (3) Quadrado(5). Agora você pode facilmente estimar. Um último exemplo; determinamos a raiz quadrada de 88: sqrt(88) = Quadrado(2 × 44) = Quadrado(2 × 4 × 11) = Quadrado(2 × 2 × 2 × 11). Temos vários 2s em nossa raiz quadrada. Como 2 é primo, podemos remover um par e colocar um 2 fora da raiz quadrada. = Nossa raiz quadrada em termos mais simples é (2) Sqrt(2 × 11) ou (2) Quadrado(2) Quadrado(11). Agora podemos aproximar Sqrt(2) e Sqrt(11) e encontrar uma resposta estimada, se quisermos. 

No nosso exemplo, o dígito mais à esquerda é o número 7. Porque sabemos que 2 = 4 7 < 3 = 9, podemos dizer que n = 2 porque é o maior inteiro cujo quadrado é menor ou igual a 7. Escreva 2 no quadrante superior direito. Este é o primeiro dígito da resposta. Escreva 4 (o quadrado de 2) no quadrante inferior direito. Este número é importante para a próxima etapa. 
Em nosso exemplo, escrevemos um 4 sob 7 e subtraímos. Isto dá 3 como resposta. 
Em nosso exemplo, o número a seguir é "80". Nota "80" ao lado do 3 no quadrante esquerdo. Em seguida, multiplique o número no canto superior direito por 2. Este número é 2, então 2 × 2 = 4. Nota "`4"` no canto inferior direito, seguido por _×_=. 
Em nosso exemplo, preenchemos 8, e isso dá 4(8) × 8 = 48 × 8 = 384. Isso é maior que 380. Então 8 é muito grande, mas 7 provavelmente não é. Preencha 7 e resolva: 4(7) × 7 = 329. 7 é bom porque 329 é menor que 380. Nota 7 no canto superior direito. Este é o segundo dígito da raiz quadrada de 780,14. 
Em nosso exemplo, subtraímos 329 de 380, e isso nos dá 51 como resultado. 
Em nossa resposta, agora escrevemos uma vírgula porque também encontramos isso em 780.14. Mova o próximo par (14) para baixo no quadrante esquerdo. 27 x 2 = 54, então escrevemos "54 _×_=" no quadrante inferior direito. 
Em nosso exemplo, 549 × 9 = 4941, que é menor ou igual ao número à esquerda (5114). 549 × 10 = 5490, que é muito alto, então 9 é nossa resposta. Escreva 9 como o próximo número no canto superior direito e subtraia o resultado da multiplicação do número da esquerda: 5114 -4941 = 173. 
Calcular a raiz quadrada de um número sem calculadora
Contente
Antes do advento das calculadoras, alunos e professores tinham que calcular raízes quadradas com caneta e papel. Várias técnicas foram desenvolvidas na época para lidar com essa tarefa às vezes pesada, com algumas fornecendo uma estimativa aproximada e outras calculando o valor exato. Continue lendo para saber como encontrar a raiz quadrada de um número em algumas etapas fáceis.
Degraus
Método 1 de 2: Enraizamento com fatores primos

1. Divida seu número em quadrados. Este método usa os fatores de um número para encontrar a raiz quadrada de um número (dependendo do número, isso pode ser uma resposta exata ou uma estimativa). O fatores de um determinado número são uma sequência aleatória de números multiplicados para formar esse número específico. Por exemplo, você pode dizer que os fatores de 8 são iguais a 2 e 4 porque 2 × 4 = 8. Quadrados perfeitos, por outro lado, são inteiros que são o produto de outros inteiros. Por exemplo: 25, 36 e 49 são quadrados perfeitos porque são iguais a 5, 6 e 7 . respectivamente. Os segundos fatores de potência são, como você deve ter entendido, fatores que também são quadrados perfeitos. Para encontrar uma raiz quadrada usando fatores primos, primeiro tente dividir o número em seus fatores cúbicos.
- Tome o seguinte exemplo. Vamos encontrar a raiz quadrada de 400. Para começar, dividimos o número em quadrados. Como 400 é um múltiplo de 100, sabemos que é divisível por 25 - um quadrado perfeito. A memorização rápida nos diz que 400 / 25 = 16. 16 também é um quadrado perfeito. Então os fatores quadráticos de 400 são 25 e 16 porque 25 × 16 = 400.
- Escrevemos isso como: Sqrt(400) = Sqrt(25 × 16)

2. Pegue as raízes quadradas de suas raízes quadradas. A regra do produto de raízes quadradas afirma que para qualquer número dado uma e b, Sqrt(a × b) = Sqrt(a) × Sqrt(b). Por causa dessa propriedade, agora podemos pegar as raízes quadradas dos fatores do cubo e multiplicá-las para obter a resposta.

3. Se o seu número não puder ser fatorado perfeitamente, simplifique-o. Na realidade, os números dos quais você deseja encontrar as raízes quadradas não serão bons números arredondados com boas raízes quadradas como 400. Nestes casos, pode não ser possível obter um número inteiro como resposta. Em vez disso, usando todos os cubos que encontrar, você pode determinar a resposta como uma raiz quadrada menor e mais fácil de usar. Você faz isso reduzindo o número a uma combinação de fatores de cubo e outros fatores e, em seguida, simplificando-o.

4. Simplifique, se necessário. Usando a raiz quadrada nos termos mais simples, geralmente é bastante fácil obter uma estimativa aproximada da resposta estimando as raízes quadradas restantes e multiplicando-as. Uma maneira de melhorar seus palpites é encontrar os quadrados perfeitos em ambos os lados do número em sua raiz quadrada. Você sabe que o valor decimal do número em sua raiz quadrada está em algum lugar entre esses dois números, então seu palpite deve estar entre esses números também.

5. Alternativamente, como primeiro passo, você pode simplificar o número para omínimo múltiplo comum. A busca por fatores quadrados não é necessária se você puder encontrar facilmente os fatores primos de um número (fatores que também são primos ao mesmo tempo). Escreva o número em termos de mínimos múltiplos comuns. Em seguida, pesquise entre seus fatores por pares correspondentes de números primos. Se você encontrar dois fatores primos que combinam, remova-os da raiz quadrada e coloque uma desses números fora do radical.
Método 2 de 2: Encontrando raízes quadradas sem calculadora
Com uma longa divisão

1. Divida os dígitos do seu número em pares. Este método é semelhante à divisão longa, que permite exato encontrar a raiz quadrada de um número dígito por dígito. Embora não seja essencial, dividir um número em partes viáveis pode facilitar a resolução, especialmente se for longo. Primeiro desenhe uma linha vertical dividindo a área de trabalho em 2 áreas, depois uma linha mais curta perto do topo da área direita, dividindo-a em uma parte superior menor e uma parte maior abaixo. Em seguida, divida o número em pares de números, começando do ponto decimal. De acordo com esta regra, 79520789182.47897 torna-se igual a "7 95 20 78 91 82,47 89 70". Escreva este número na área superior esquerda.
- Como exemplo, vamos calcular a raiz quadrada de 780,14. Divida seu espaço de trabalho conforme indicado acima e anote "7 80, 14" no canto superior esquerdo. Tudo bem se houver apenas um número na extrema esquerda, em vez de dois. Você então escreve a resposta (a raiz quadrada de 780,14) no topo da área direita.

2. Encontre o maior inteiro n cujo quadrado é menor ou igual ao dígito ou número mais à esquerda. Encontre o maior quadrado que é menor ou igual a este número, então encontre a raiz quadrada deste quadrado. Este número é n. Observe que na área superior direita e escreva o quadrado de n no quadrante inferior dessa área.

3. Subtraia o número que você calculou do dígito ou número mais à esquerda. Tal como acontece com a divisão longa, o próximo passo é subtrair o quadrado do número que acabamos de calcular. Escreva este número sob o número mais à esquerda e subtraia-os um do outro. Escreva a resposta abaixo.

4. Mover o próximo número para baixo. Coloque-o ao lado do valor encontrado na edição anterior. Multiplique o número no canto superior direito por dois e anote no canto inferior direito. Economize espaço ao lado do número que você acabou de anotar para a soma da multiplicação que você fará na próxima etapa. Escreva aqui `"_×_="`.

5. Digite os números à direita. No espaço vazio da soma (à direita), insira o maior inteiro que fará com que o resultado da soma da multiplicação à direita seja menor ou igual ao número atual à esquerda.

6. Subtraia o número que você acabou de calcular do número atual à esquerda. Então você subtrai o resultado da multiplicação à direita da resposta atual à esquerda. Escreva sua resposta diretamente abaixo.

7. Repita o passo 4. Mova o próximo par de números de 780,14 para baixo. Se você chegar a uma vírgula, escreva essa vírgula na resposta à direita. Em seguida, multiplique o número no canto superior direito por 2 e escreva a resposta ao lado de ("_ × _") como acima.

8. Repita os passos 5 e 6. Encontre o maior número que dá uma resposta menor ou igual ao número atual à esquerda. Resolver.

9. Para tornar o resultado preciso, repita o procedimento anterior até encontrar a resposta com o número de casas decimais (centésimos, milésimos) que você precisa.
Entendendo o procedimento
- Observe que se você dividir 88962 por 7 usando a divisão longa, o primeiro passo é o mesmo: você está lidando com o primeiro dígito de 88962 (8) e deseja que o maior dígito multiplicado por 7 seja menor ou igual a 8. Essencialmente você decide d de modo que 7×d ≤ 8 < 7×(d+1). Neste caso d é igual a 1.
- Em nosso exemplo (10A+B)² = L = S = 100A² + 2×10A×B + B². Lembre-se que 10A+B representa nossa resposta L junto com B na posição das unidades e A na posição das dezenas. Por exemplo, se A=1 e B=2, então 10A+B é o número 12. (10A+B)² é a área de todo o quadrado, enquanto 100A² é a área do maior quadrado interno, B² é a área do menor quadrado e 10A×B é a área de cada um dos retângulos restantes. Através deste procedimento longo e complicado, podemos encontrar a área de todo o quadrado somando as áreas dos quadrados e retângulos que o compõem.

1. Considere o número cuja raiz quadrada você deseja calcular como a área S de um quadrado. Como a área de um quadrado é L, onde L é o comprimento de um de seus lados, então, tirando a raiz quadrada do seu número, você tenta calcular o comprimento L do lado desse quadrado.

2. Dê a cada dígito da sua resposta uma letra. Dê a variável A como o primeiro dígito de L (a raiz quadrada que estamos tentando calcular). B é o segundo dígito, C é o terceiro, e assim por diante.

3. Entregue uma carta a cada "par de números" do número com o qual você começa. Dê a variável Suma ao primeiro par de dígitos em S (o valor inicial), Sb para o segundo par de dígitos, etc.

4. Entenda a relação entre esse método e a divisão longa. Esse método de encontrar uma raiz quadrada é essencialmente uma divisão longa, dividindo o valor inicial por sua raiz quadrada e tomando a raiz quadrada como resposta "dado". Assim como na divisão longa, onde você está interessado apenas no próximo dígito de cada vez, você está interessado apenas nos próximos dois dígitos de cada vez (que correspondem ao próximo dígito da raiz quadrada).

5. Encontre o maior número cujo quadrado é menor ou igual a Suma é. O primeiro dígito A em nossa resposta é então o maior inteiro cujo quadrado não é maior que Suma (A tal que A² ≤ Sa < (A+1)²). Em nosso exemplo, S. éuma = 7 e 2² ≤ 7 < 3², então A = 2.

6. Visualize o quadrado que você deseja encontrar a área de. Sua resposta, a raiz quadrada do valor inicial, é L, descrevendo o comprimento de um quadrado de área S (o valor inicial). Os valores para A, B e C representam os números no valor L. Outra maneira de dizer isso é que para uma resposta de 2 dígitos, 10A + B = L, e para uma resposta de 3 dígitos, 100A +10B + C = L, e assim por diante.

7. Subtraia A² de Suma. Traga um par de números (Sb) abaixo do número S. suma sb é quase a área total do quadrado, da qual você acabou de subtrair a área do maior quadrado interno. O resto é dizer o número N1, que obtivemos na etapa 4 (N1 = 380 em nosso exemplo). N1 é igual a 2×10A×B + B² (a área dos 2 retângulos mais a área do pequeno quadrado).

8. Veja N1 = 2×10A×B + B², também escrito como N1 = (2×10A + B) × B. Em nosso exemplo você já conhece N1 (380) e A (2), então agora você precisa encontrar B. B provavelmente não é um número inteiro, então você precisa na verdade encontre o maior inteiro B, tal que (2×10A + B) × B ≤ N1. Então agora você tem: N1 < (2×10A + (B+1)) × (B+1).)

9. Resolva a equação. Para resolver esta equação, multiplique A por 2, desloque-o para as dezenas (multiplique por 10), coloque B nas unidades e multiplique o resultado por B. Em outras palavras, (2 × 10A + B) × B. Isso é exatamente o que você faz quando escreve "N_×_=" (com N=2×A) no quadrante inferior direito na etapa 4. Na etapa 5, você determina o maior inteiro B que se encaixa abaixo da linha, tal que (2×10A + B) × B ≤ N1.

10. Subtraia a área (2×10A + B) × B da área total. Isso produz a área S-(10A+B)² que você ainda não levou em consideração (e que você usa para calcular os seguintes números da mesma maneira).

11. Para calcular o próximo dígito C, repita o procedimento. Mova o próximo par de números de S para baixo (Sc) para obter N2 à esquerda e procure o maior C, então agora você tem: (2×10×(10A+B)+C) × C ≤ N2 (igual a duas vezes o número de dois dígitos "A B" Seguido por "_×_=" . Agora determine o maior número que você pode inserir aqui, que lhe dará uma resposta menor ou igual a N2.
Pontas
- Movendo o ponto decimal duas casas (um fator de 100) move o ponto decimal na raiz quadrada correspondente em uma casa (um fator de 10).
- No exemplo, 1,73 pode ser considerado como "descanso": 780,14 = 27,9² + 1,73.
- Este método funciona para qualquer sistema numérico, não apenas o sistema decimal (dez decimais).
- Sinta-se à vontade para colocar os cálculos onde quiser. Algumas pessoas escrevem acima do número que querem calcular a raiz quadrada de.
- Um método alternativo é o seguinte: √z = √(x^2+y) = x + y/(2x + y/(2x + y/(2x) + ...))). Por exemplo, para calcular a raiz quadrada de 780,14, você pegaria o número inteiro ao quadrado mais próximo de 780,14 (28), então =780,14, x=28 e y=-3,86. Preencher e estimar nos dá x + y/(2x) e isso dá (termos simplificados) 78207/2800 ou cerca de 27.931(1); o próximo mandato, 4374188/156607 ou cerca de 27.930986(5). Cada termo adiciona aproximadamente 3 casas decimais de precisão ao anterior.
Avisos
- Certifique-se de dividir o número em pares a partir do ponto decimal. Dividindo 79520789182.47897 como "79 52 07 89 18 2.4 78 97" dá um resultado que não está correto.
Artigos sobre o tópico "Calcular a raiz quadrada de um número sem calculadora"
Оцените, пожалуйста статью
Similar
Popular