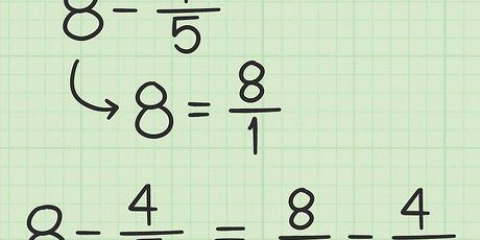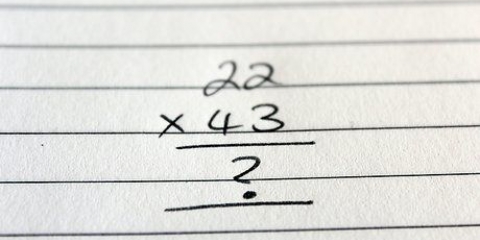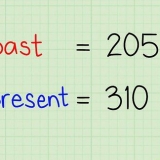Subtraindo Números

Contente

Degraus
Pontas
Avisos

Subtrações são aquelas somas em que você subtrai dois números um do outro. É bem simples se você quiser subtrair números inteiros uns dos outros, mas fica um pouco mais complicado quando você está trabalhando com frações ou decimais. Depois de dominar a subtração, você pode passar para os conceitos matemáticos mais complicados e adicionar, multiplicar e dividir números será muito mais fácil.

Degraus

Método 1 de 6: Subtraia inteiros grandes por empréstimo

1. Anote o número maior. Suponha que você trabalhe com a soma 32 - 17. Anote 32 primeiro.

2. Escreva o número menor diretamente abaixo dele. Certifique-se de que as dezenas e as unidades estejam bem alinhadas de modo que o 3 em "32" diretamente acima de 1 em "17" estado, e os 2 em "32" diretamente acima do "7" aos 17.

3. Subtraia o número inferior do superior. Isso pode ser um pouco complicado se o número de baixo for maior que o de cima. Neste caso 7 é maior que 2. Aqui está o que fazer:

voce terá que "emprestar" dos 3 em "32" fazer o 2 a 12.

Atravesse o 3 de "32" e faça um 2, então faça a unidade 2 um 12.

Agora você tem 12 – 7 = 5. Escreva um 5 sob a coluna de unidades.

4. Subtraia o dez no número inferior do dez no número superior. Não se esqueça que o 3 de 32 se tornou um 2. Agora subtraia o 1 em 17 do 2 acima dele, então 2-1 = 1. Escreva 1 na coluna das dezenas. Se tudo estiver bem, agora você tem 15 como resposta, então 32 - 17 = 15.

5. Verifique seu trabalho. Se você quiser ter certeza de que fez o cálculo corretamente, tudo o que você precisa fazer é adicionar a resposta ao menor número para obter o maior número de volta. Então, para verificar: 15 + 17 = 32, então você fez certo. Excelente!

Método 2 de 6: subtraia pequenos números inteiros

1. Determine qual número é maior. Um exercício como 15 - 9 requer uma abordagem diferente de 2 - 30.

Na soma 15 - 9, o primeiro número, 15, é o maior.
Na soma 2 - 30, o segundo número, 30 é o maior.

2. Decida se sua resposta deve ser positiva ou negativa. Se o primeiro número for o maior, então a resposta é positiva. Se o segundo número for o maior, a resposta é negativa.

Então na primeira soma, 15 - 9, a resposta se torna positiva, porque 15 é maior que 9.

Então, na segunda soma, 2 - 30, a resposta se torna negativa, porque 2 é menor que 30.

3. Encontre a diferença entre os dois números. Para subtrair dois números, calcule a diferença entre eles.

Para o problema 15 - 9, pegue 15 moedas. Remova 9 e conte quantos restam (6). Então, 15 - 9 = 6. Ou use uma linha numérica e desenhe os números de 1 a 15 ao longo da linha, depois risque 9 de 15 para baixo para chegar a 6.

Com a soma 2 – 30 é mais fácil virar os números e dar a resposta negativa. Então, 30 - 2 = 28, e com isso 2 - 30 é -28.

Método 3 de 6: Subtraindo decimais

1. Escreva o número maior acima do número menor para que os decimais fiquem alinhados. Suponha que você tenha o seguinte problema: 10,5 - 8,3. Escreva o 10,5 acima de 8,3 de forma que as vírgulas fiquem uma acima da outra.

Se você tiver um problema em que um número tem mais casas decimais que o outro, preencha o espaço vazio com zeros. Por exemplo, se você tiver o problema 5,32 - 4,2, você pode reescrevê-lo como 5,32 = 4,20. Isso não altera o valor de um número, mas você garante que ambos os números possam ser subtraídos mais facilmente um do outro.

2. Subtraia os décimos um do outro. A subtração desses números é a mesma que com os inteiros, exceto que você deve prestar atenção ao ponto decimal, alinhado e incluído na resposta. Neste caso você tem que subtrair 3 de 5. 5 - 3 = 2, então você escreve um 2 sob o 3 em 8,3.

Não se esqueça de incluir o ponto decimal (a vírgula) na resposta. Agora fica assim: ,2.

3. Agora subtraia as unidades umas das outras. Agora subtraia 8 de 0. Pegue emprestado uma dúzia do 1 (ao lado do 0) para fazer 10, agora subtraia 8 de 10. Você também pode calcular imediatamente a soma 10 – 8 = 2, sem a etapa intermediária de empréstimo, porque o número inferior não possui dez. Escreva a resposta em 8.

4. Então a resposta final será 2,2.

Método 4 de 6: Subtraindo frações

1. Junte os numeradores e os denominadores. Suponha que você esteja trabalhando com o problema 13/10 - 3/5. Escreva este problema de modo que ambos os numeradores, 13 e 3, e ambos os denominadores, 10 e 5, estejam próximos um do outro, separados por um sinal de menos. Isso lhe dá uma melhor visão geral do problema e torna mais fácil encontrar uma solução.

2. Encontre o mínimo múltiplo comum. Este é o menor múltiplo de dois números. O LCF de 10 e 5 neste exemplo é 10.

Observe que o lcm de dois números nem sempre é um dos dois números. Por exemplo, em 3 e 2, o LCF é 6, porque não há número menor que 6 que é um múltiplo de cada um dos números.

3. Reescreva as frações com os mesmos denominadores. A fração 13/10 pode permanecer inalterada porque o denominador não mudou, mas a fração 3/5 se torna igual a 6/10 porque o denominador vai duas vezes para o múltiplo comum de 10. Agora você igualou as duas frações. 3/5 é igual a 6/10, mas com a diferença de que agora não é mais um problema subtrair as duas frações uma da outra.

Então a nova tarefa será: 13/10 - 6/10.

4. Subtraia ambos os numeradores um do outro. Então 13 - 6 = 7. Não subtraia os denominadores.

5. Coloque o novo numerador acima do novo denominador (o LCF calculado anteriormente) para a resposta final. O novo numerador é 7 e o denominador de ambas as frações é 10. Então a resposta final é 7/10.

6. Verifique seu trabalho. Se você quiser ter certeza de que fez o cálculo corretamente, tudo o que você precisa fazer é adicionar a resposta ao menor número para obter o maior número de volta. Então, para verificar: 7/10 + 6/10 = 13/10. Agora você está pronto.

Método 5 de 6: Subtraia uma fração de um número inteiro

1. Escreva a tarefa. Suponha que temos o seguinte problema: 5 - 3/4. Observe isso.

2. Converta o número inteiro em uma fração com o mesmo denominador da fração dada. Faça uma fração do 5 com o denominador 4. Primeiro considere que 5 é igual à fração 5/1. Então você multiplica o numerador e o denominador da nova fração por 4 para obter duas frações com o mesmo denominador. Isso mantém o valor da fração igual, mas com números diferentes. Então, 5/1 x 4/4 = 20/4.

3. Reescreva a tarefa. Isso agora pode ser escrito como: 20/4 - 3/4.

4. Subtraia os numeradores das frações e mantenha as frações iguais. Então, 20 - 3 = 17. Então o numerador final se torna 17 e o denominador é 4.

5. Então a resposta para o problema é 17/4. Para converter essa fração imprópria em uma fração composta, divida 17 por 4 para obter o número 4 com resto 1. A resposta fica assim: 4 1/4.

Método 6 de 6: Subtraindo Variáveis

1. Escreva a tarefa. Suponha que você esteja trabalhando no seguinte problema: 3x - 5x + 2y - z - (2x + 2x + y). Escreva a primeira equação acima da segunda.

2. Subtraia todos os termos semelhantes uns dos outros. Ao trabalhar com variáveis, você só pode subtrair termos com a mesma variável e com o mesmo poder. Isso significa que você pode fazer 4x -7x, mas não 4x -7x. Então você pode dividir essa tarefa assim:

3x - 2x = x

-5x - 2x = -7x

2y - y = y

-z - 0 = -z

3. Dê sua resposta final. Agora que você subtraiu todos os termos iguais, você pode imediatamente dar sua resposta final. Aqui está a resposta:

3x - 5x + 2y - z - (2x + 2x + y) = x - 7x + y - z

Pontas

Divida números maiores em pedaços menores. Tirar: 63 - 25.Ninguém está dizendo que você tem que subtrair todos os 25 de uma vez. Você pode primeiro subtrair 3 para obter 60; então subtraia 20 para obter 40 e depois os últimos 2. Resultado: 38. E agora você não precisa pedir emprestado.

Avisos

Se você tem uma mistura de números positivos e negativos, as coisas ficam muito mais complicadas.Continue procurando artigos que possam te ajudar com isso.