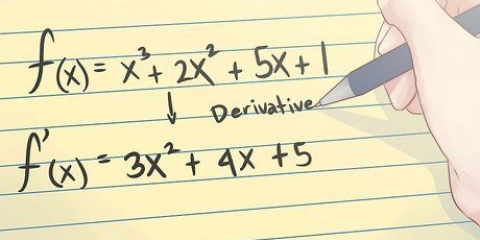(Escreva a função original.)
(Escreva a função original.) (Reescreva a raiz como um expoente.)
(Reescreva a raiz como um expoente.) (Encontre a derivada usando a regra da potência.)
(Encontre a derivada usando a regra da potência.) (Simplifique o expoente.)
(Simplifique o expoente.)
Continuando com a raiz quadrada da função x de cima, a derivada pode ser simplificada da seguinte forma: 




Por exemplo: suponha que você tenha a derivada de  quero encontrar. Em seguida, defina as duas partes da seguinte forma:
quero encontrar. Em seguida, defina as duas partes da seguinte forma: 





Em seguida, determine a derivada da segunda função: 







Na função  , é o número raiz
, é o número raiz  . A derivada é
. A derivada é  .
. Na função  , é o número raiz
, é o número raiz  . A derivada é
. A derivada é  .
. Na função  , é o número raiz
, é o número raiz  . A derivada é
. A derivada é  .
. 
E se  , então
, então 
E se  , então
, então 
E se  , então
, então 

E se  , então
, então 
E se  , então
, então 
E se  , então
, então 

E se  , então
, então 
E se  , então
, então 
E se  , então
, então 
Encontrando a derivada da raiz quadrada de x
Contente
Se você estudou matemática na escola, deve ter aprendido a regra da potência para determinar a derivada de funções simples. No entanto, quando a função contém uma raiz quadrada ou radical, como 
Degraus
Método 1 de 3: Aplicando a regra de potência

1. Dê outra olhada na regra de potência para derivadas. A primeira regra que você provavelmente aprendeu para encontrar derivadas é a regra da potência. Esta regra diz que para uma variável  à potência de um número
à potência de um número  , é a derivada, e é calculada da seguinte forma:
, é a derivada, e é calculada da seguinte forma:
 à potência de um número
à potência de um número  , é a derivada, e é calculada da seguinte forma:
, é a derivada, e é calculada da seguinte forma: - Dê uma olhada nas seguintes funções de exemplo e suas derivadas:
- E se
, então
- E se
, então
- E se
, então
- E se
, então

2. Reescreva a raiz quadrada como expoente. Para encontrar a derivada de uma função de raiz quadrada, lembre-se de que a raiz quadrada de um número ou variável também pode ser escrita como um expoente. O termo sob o radical é escrito como uma base e é elevado à potência 1/2. O termo também é usado como um expoente da raiz quadrada. Observe os exemplos a seguir:




3. Aplicar a regra do poder. Se a função é a raiz quadrada mais simples,  , então aplique a regra da potência da seguinte forma para encontrar a derivada:
, então aplique a regra da potência da seguinte forma para encontrar a derivada:
 , então aplique a regra da potência da seguinte forma para encontrar a derivada:
, então aplique a regra da potência da seguinte forma para encontrar a derivada: (Escreva a função original.)
(Escreva a função original.) (Reescreva a raiz como um expoente.)
(Reescreva a raiz como um expoente.) (Encontre a derivada usando a regra da potência.)
(Encontre a derivada usando a regra da potência.) (Simplifique o expoente.)
(Simplifique o expoente.)
4. Simplifique o resultado. Nesta fase, você deve saber que um expoente negativo significa que você toma o inverso do que seria o número com o expoente positivo. O expoente de  significa que a raiz quadrada da base se torna o denominador de uma fração.
significa que a raiz quadrada da base se torna o denominador de uma fração.
 significa que a raiz quadrada da base se torna o denominador de uma fração.
significa que a raiz quadrada da base se torna o denominador de uma fração.


Método 2 de 3: Aplicando a regra da cadeia para funções de raiz quadrada

1. Revisar a regra da cadeia para funções. A regra da cadeia é uma regra para derivadas que você usa quando a função original combina uma função dentro de outra função. A regra da cadeia diz que, para duas funções  e
e  , a derivada da combinação das duas funções pode ser encontrada da seguinte forma:
, a derivada da combinação das duas funções pode ser encontrada da seguinte forma:
 e
e  , a derivada da combinação das duas funções pode ser encontrada da seguinte forma:
, a derivada da combinação das duas funções pode ser encontrada da seguinte forma: - E se
, então
.

2. Defina as funções da regra da cadeia. O uso da regra da cadeia exige que você primeiro defina as duas funções que compõem sua função combinada. Para funções de raiz quadrada, a função mais externa é  a função raiz quadrada e a função mais interna
a função raiz quadrada e a função mais interna  a função sob o radical.
a função sob o radical.
 a função raiz quadrada e a função mais interna
a função raiz quadrada e a função mais interna  a função sob o radical.
a função sob o radical. quero encontrar. Em seguida, defina as duas partes da seguinte forma:
quero encontrar. Em seguida, defina as duas partes da seguinte forma:


3. Encontre as derivadas das duas funções. Para aplicar a regra da cadeia à raiz quadrada de uma função, você deve primeiro encontrar a derivada da função raiz quadrada geral:






4. Combine as funções na regra da cadeia. A regra da cadeia é  . Combine as derivadas da seguinte forma:
. Combine as derivadas da seguinte forma:
 . Combine as derivadas da seguinte forma:
. Combine as derivadas da seguinte forma:


Método 3 de 3: Encontrando as derivadas das funções de raiz rapidamente

1. Determinar derivadas de uma função de raiz quadrada usando um método rápido. Quando você deseja encontrar a derivada da raiz quadrada de uma variável ou função, pode aplicar uma regra simples: a derivada sempre será a derivada do número sob o radical, dividido pelo dobro da raiz quadrada original. Simbolicamente, isso pode ser representado como:
- E se
, então

2. Encontre a derivada do número sob o radical. Este é um número ou função sob o sinal da raiz quadrada. Para usar este método rápido, basta encontrar a derivada do número sob o radical. Confira os exemplos a seguir:
 , é o número raiz
, é o número raiz  . A derivada é
. A derivada é  .
. , é o número raiz
, é o número raiz  . A derivada é
. A derivada é  .
. , é o número raiz
, é o número raiz  . A derivada é
. A derivada é  .
.
3. Escreva a derivada do número raiz como o numerador de uma fração. A derivada de uma função de raiz quadrada conterá uma fração. O numerador desta fração é a derivada do número raiz. Então, nas funções de exemplo acima, a primeira parte da derivada ficará assim:
 , então
, então 
 , então
, então 
 , então
, então 

4. Escreva o denominador como o dobro da raiz quadrada original. Com este método rápido, o denominador é duas vezes a função raiz quadrada original. Assim, nas três funções de exemplo acima, os denominadores das derivadas são:
 , então
, então 
 , então
, então 
 , então
, então 

5. Combine o numerador e o denominador para encontrar a derivada. Junte as duas metades da fração e o resultado será a derivada da função original.
 , então
, então 
 , então
, então 
 , então
, então 
Artigos sobre o tópico "Encontrando a derivada da raiz quadrada de x"
Оцените, пожалуйста статью
Popular