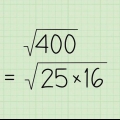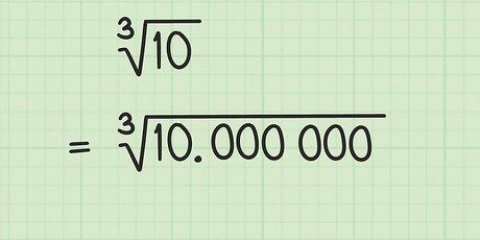Como Calcular uma Raiz Quadrada Sem Calculadora

Contente

Degraus
Pontas

Calcular a raiz quadrada é fácil ao lidar com um número inteiro. Caso contrário, existe um procedimento lógico que você pode seguir para calcular a raiz quadrada sistematicamente, com ou sem calculadora. No entanto, para isso você deve primeiro multiplicar, adicionar e dividir.

Degraus

Método 1 de 3: Determinando a raiz quadrada de um número inteiro

Imagem intitulada Encontre uma raiz quadrada sem uma calculadora Passo 1

1. Encontre a raiz quadrada perfeita com uma multiplicação. O raiz quadrada de um número é qualquer número que, multiplicado por ele mesmo, é igual ao primeiro número. Outra maneira de dizer isso é: `O que podemos fazer com nós mesmos? multiplicar para obter o número da atribuição?`

Por exemplo, a raiz quadrada de 1 é 1, porque 1 multiplicado por 1 é igual a 1 (1 x 1=1). No entanto, a raiz quadrada de 4 é 2, porque 2 multiplicado por 2 é igual a 4 (2 x 2 = 4). Pense no conceito de raiz quadrada imaginando um carvalho. Um carvalho cresce de uma bolota. Portanto, é maior que, mas relacionado à bolota, que está na raiz da árvore. No exemplo acima, 4 é a raiz e 2 é a bolota.
Então a raiz quadrada de 9 é 3 (3 x 3=9), de 16 é 4 (4 x 4=16), de 25 é 5 (5 x 5=25), de 36 é 6 (6 x 6=36 ), de 49 é 7 (7 x 7=49), de 64 é 8 (8 x 8=64), de 81 é 9 (9 x 9=81), e de 100 é 10 (10 x 10=100).

Imagem intitulada Encontre uma raiz quadrada sem uma calculadora Passo 2

2. Usopartes para encontrar a raiz quadrada. Para encontrar a raiz quadrada de um inteiro, você pode dividir o inteiro até obter uma resposta que seja igual ao número pelo qual você divide o inteiro.

Por exemplo: 16 dividido por 4 é 4, e 4 dividido por 2 é 2, etc. Então, nesses exemplos, 4 é a raiz quadrada de 16 e 2 é a raiz quadrada de 4.

Raízes quadradas perfeitas não têm frações ou decimais, porque são números inteiros.

Imagem intitulada Encontre uma raiz quadrada sem uma calculadora Passo 3

3. Use os símbolos corretos para a raiz quadrada. Os matemáticos usam um símbolo especial, o sinal de radical, para indicar a raiz quadrada. Isso se parece com uma marca de seleção com uma linha horizontal no topo apontando para a direita.

N é igual ao número que você deseja determinar a raiz quadrada de. Isso será colocado dentro do sinal de radical (abaixo da linha horizontal).

Então, se você quer encontrar a raiz quadrada de 9, você escreve a fórmula com o `N` (9) dentro do radical, então um sinal de igual e o 3. Isso significa que a `raiz quadrada de 9 é igual a 3.`

Método 2 de 3: Encontrando a raiz quadrada de outros números

Imagem intitulada Encontre uma raiz quadrada sem uma calculadora Passo 4

1. Faça uma estimativa e use um processo de eliminação. É mais difícil determinar as raízes quadradas de números que não sejam inteiros. Mas é possível.

Suponha que você queira determinar a raiz quadrada de 20. Você sabe que 16 é um inteiro perfeito cuja raiz quadrada é 4 (4 x 4=16). Da mesma forma, 25 tem a raiz quadrada de 5 (5 x 5 = 25), então a raiz quadrada de 20 deve cair em algum lugar entre.
Você pode estimar que a raiz quadrada de 20 é igual a 4,5. Agora você quadrado 4,5 para verificar sua resposta. Isso significa multiplicar o número por ele mesmo: 4,5 x 4,5. Verifique se esta resposta está acima ou abaixo de 20. Se seu palpite parecer errado, tente outro palpite (talvez 4,6 ou 4,4) e reduza seu palpite até chegar a 20.
Por exemplo, 4,5 x 4,5 = 20,25, então você deve tentar um número menor, algo como 4,4. 4,4 x 4,4 = 19,36. Então a raiz quadrada ou de 20 está entre 4,5 e 4,4. Que tal 4,445 x 4,445? Isso é 19.758. Estamos nos aproximando. Se você continuar fazendo isso, eventualmente chegará a 4,475 x 4,475 = 20,03. Arredondado, são 20.

Imagem intitulada Encontre uma raiz quadrada sem uma calculadora Passo 5

2. Usar médias. Em princípio, você também tenta encontrar os inteiros mais próximos entre os quais seu número cai.

Em seguida, divida seu número por um dos números de raiz quadrada. Pegue a resposta e encontre a média desse número e o número pelo qual você dividiu (a média é a soma de dois números dividido por dois). Em seguida, pegue o número original e divida-o pela média que você obteve. No final você encontra a média dessa resposta com a primeira média que você obteve.

Isso soa complicado? Um exemplo é provavelmente mais fácil de seguir. Por exemplo, 10 está entre os dois quadrados perfeitos 9 (3 x 3=9) e 16 (4 x 4=16). As raízes quadradas desses números são 3 e 4. Então divida 10 pelo primeiro número, 3. Isso dá 3,33. Pegue a média de 3 e 3,33 (somar e dividir por dois). Isso dá 3,1667. Agora divida 10 por 3,1667. A resposta é 3,1579. Pegue a média de 3,1579 e 3,1667. Agora você receberá 3,1623 como resposta.

Verifique seu trabalho multiplicando sua resposta (neste caso 3,1623) por ela mesma. E de fato: 3,1623 multiplicado por 3,1623 é igual a 10,001.

Método 3 de 3: Quadrando números negativos

Imagem intitulada Encontre uma raiz quadrada sem uma calculadora Passo 6

1. Números negativos quadrados usando o mesmo processo. Lembre-se que um número negativo multiplicado por um número negativo produz um número positivo. Então, elevar ao quadrado um número negativo formará um número positivo.

Por exemplo, -5 x -5 =25. No entanto, lembre-se que 5 x 5 = 25. Então a raiz quadrada de 25 é -5 ou 5. Em princípio, esse número tem duas raízes quadradas.
Da mesma forma, 3 x 3=9 e -3 x -3=9, então a raiz quadrada de 9 é 3 e -3. O número positivo tem a raiz primária, então neste ponto a única resposta que você precisa é.

Imagem intitulada Encontre uma raiz quadrada sem uma calculadora Passo 7

2. Finalmente, use uma calculadora. É bom entender como fazer esses cálculos à mão, mas existem muitas calculadoras online que podem calcular a raiz quadrada de um número.

Veja também se sua calculadora regular tem um símbolo de raiz quadrada.

Uma calculadora online pedirá que você insira o número do qual deseja calcular a raiz quadrada e pressione um botão específico. O computador então gera a raiz quadrada desse número.

Pontas

É altamente recomendável memorizar os primeiros quadrados perfeitos:

0=0, 1=1, 3=9, 4=16, 5=25, 6=36, 7=49, 8=64, 9=81, 10=100,
Aprenda também: 11=121, 12=144, 13 169, 14=196, 15=225, 16=256, 17=289...
Mais exemplos para facilitar a matemática: 10=100, 20=400, 30=900, 40=1600, 50=2500, ...