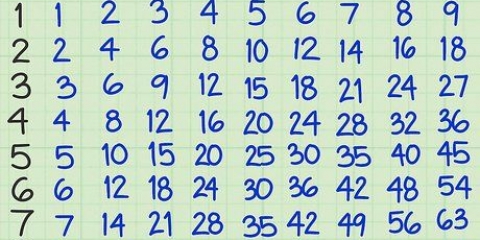
Se encaixa 15 em 34? Sim, claro, e assim podemos começar a calcular a resposta. (O primeiro número não precisa se encaixar perfeitamente, só precisa ser menor que o segundo número). 
Precisamos resolver 34 ÷ 15, ou `quantas vezes 15 cabe em 34`? Você está procurando um número que pode ser multiplicado por 15 para obter um número menor que 34, mas bem próximo: Funciona 1? 15 x 1 = 15, isso é menos que 34, mas continue adivinhando. Funciona 2? 15 x 2 = 30. Isso ainda é menor que 34, então 2 é uma resposta melhor do que 1. Funciona 3? 15 x 3 = 45, maior que 34. Muito alto! A resposta é 2. 
Como você está calculando 34 ÷ 15, você escreveria como resposta, 2, na linha de resposta acima do `4`. 
Sua resposta foi 2 e o menor número no problema é 15, então calculamos 2 x 15 = 30. Escreva `30` em `34`. 
Resolva 34 – 30 e escreva a resposta abaixo em uma nova linha. A resposta é 4. Este 4 ainda é `o resto` depois de dividir 34 por 15 duas vezes, então vamos usá-lo na próxima etapa. 
Deixe o 4 onde está e abaixe o `7` de `3472` para fazer 47. 
Resolvemos: 47 ÷ 15: 47 é maior que nosso último número, então a resposta será maior. Vamos tentar quatro: 15 x 4 = 60. Não, muito grande! Em vez disso, tentamos três: 15 x 3 = 45. Menor que 47, mas perto disso. Perfeito. A resposta é 3, então escrevemos isso acima do `7` na linha de resposta. (Se terminarmos com uma soma como 13 ÷ 15, onde o primeiro número é menor, temos que reduzir um terceiro dígito antes de poder resolvê-lo). 
Lembre-se, calculamos 47 ÷ 15 = 3 e agora queremos encontrar o que resta: 3 x 15 = 45, então escreva `45` em 47. 47 - 45 = 2. Escreva `2` abaixo de 45. 
O próximo problema é 2 ÷ 15, o que não faz muito sentido. Abaixe um número para torná-lo 22 ÷ 15. 15 vai para 22 uma vez, então escrevemos `1` como o último dígito da resposta. Nossa resposta agora é 231. 
1 x 15 = 15, então escreva 15 sob 22. Calcular 22 - 15 = 7. Não há mais números para anotar, então, em vez de continuar a dividir, escrevemos `rest 7` após nossa resposta. A resposta final: 3472 ÷ 15 = 231 restante 7.


Se você achar isso difícil, basta contar em triplicado e adicionar um 0 no final. Conte até ficar maior que o maior número do problema (143) e pare por aí. 
30 (um dedo), 60 (dois dedos), 90 (três dedos), 120 (quatro dedos). Então 30x quatro = 120. 150 (cinco dedos), então 30 x cinco = 150. 4 e 5 são as duas respostas mais prováveis para o nosso problema. 
27 x 4 = 108 27 x 5 = 135 
27 x 6 = 162. Isso é maior que 143, então não pode ser a resposta certa. 27 x 5 chegou mais perto sem ultrapassar, então 143 ÷ 27 = 5 (mais um resto 8, porque 143-135 = 8).
Dividir por um número com dois ou mais dígitos
Contente
Dividir por um número com dois ou mais dígitos é muito semelhante à divisão longa com um dígito, mas leva um pouco mais de tempo e requer um pouco mais de prática. Como a maioria de nós não se lembra da tabela de 47, isso exige um pouco de adivinhação, mas há um truque legal que você pode aprender para fazer isso mais rápido. Também fica mais fácil com alguma prática, então não fique frustrado se parecer lento no começo.
Degraus
Parte 1 de 2: Dividindo por um número de dois dígitos

1. Olhe para o primeiro dígito do número maior. Escreva o problema como divisão longa. Como um problema de divisão mais simples, você basicamente olha para o número menor e se pergunta: "Ele se encaixa no primeiro dígito do número maior??`
- Suponha que você tenha o problema 3472 ÷ 15. Cabe 15 em 3? Como 15 é definitivamente maior que 3, a resposta é `não` e vamos para o próximo passo.

2. Olhe para os dois primeiros números. Como um número de dois dígitos não pode caber em um número de um dígito, vamos agora olhar para dois dígitos, assim como faríamos com um problema de divisão regular. Se ainda for impossível dividir, você terá que olhar para os três primeiros dígitos, mas no nosso exemplo não é necessário:

3. Use algumas suposições. Verifique quantas vezes o primeiro número se encaixa no outro. Você pode já saber a resposta, mas se não, faça uma estimativa e verifique sua resposta com uma multiplicação.

4. Escreva a resposta acima do último número que você usou. Escrever isso como uma divisão longa deve parecer familiar.

5. Multiplique sua resposta pelo número menor. Isso é o mesmo que a divisão longa normal, mas aqui estamos usando um número de dois dígitos.

6. Subtraia os dois números um do outro. A última coisa que você escreveu foi abaixo do número maior original (ou parte dele). Trate isso como uma soma negativa e escreva a resposta abaixo em uma nova linha.

7. Abaixe o próximo número. Assim como um problema de divisão regular, continuamos calculando o próximo dígito da resposta até terminarmos.

8. Resolva o seguinte subproblema. Para obter o próximo número, repita os mesmos passos acima para o novo problema. Você pode voltar a estimar para encontrar a resposta:

9. Continuar com divisão longa. Repita a divisão longa como fizemos antes para multiplicar nossa resposta pelo número menor, escreva o resultado abaixo do número maior e subtraia-o para o próximo resto.

10. Determine o último dígito. Como antes, reduzimos o próximo dígito do problema original para que possamos resolver o próximo subproblema. Repita as etapas acima até encontrar todos os dígitos da resposta.

11. Determinar o resto. Agora apenas uma soma negativa para encontrar o descanso final, e terminamos. Na verdade, se a resposta para a soma negativa for 0, você não precisa escrever nenhum resto.

Parte 2 de 2: Aprendendo a estimar bem

1. Arredonde para a dezena mais próxima. Nem sempre é fácil ver quantas vezes um número de dois dígitos cabe em um número maior. Um truque útil é arredondar para o múltiplo de 10 mais próximo para facilitar a adivinhação. Isso é útil para problemas de divisão menores ou divisão longa.
- Por exemplo, digamos que precisamos resolver 143 ÷ 27, mas não sabemos quantas vezes 27 cabe em 143. Então vamos fingir que temos que resolver 143 ÷ 30.

2. Conte o número menor em seus dedos. No nosso exemplo podemos começar a calcular com 30 e não com 27. Contar em passos de 30 é bem fácil quando você pega o jeito: 30, 60, 90, 120, 150.

3. Determine as duas respostas mais prováveis. O número não se encaixava exatamente em 143, mas conhecemos números próximos: 120 e 150. Vamos ver quantos dedos temos que contar para chegar lá:

4. Teste esses dois números com o problema real. Agora que temos dois bons palpites, podemos testá-los no problema original, 143 ÷ 27:

5. Certifique-se de que você não pode chegar mais perto. Como ambos os números terminam abaixo de 143, podemos tentar chegar ainda mais perto tentando mais uma multiplicação:

Pontas
- Se você não quiser multiplicar manualmente durante a divisão longa, tente dividir o problema em números e resolver cada parte de cor. Por exemplo, 14 x 16 = (14 x 10) + (14 x 6). Anote 14 x 10 = 140 para não esquecer. Então: 14 x 6 = (10 x 6) + (4 x 6). 10 x 6 = 60 e 4 x 6 = 24. Faça 140 + 60 + 24 = 224 e você terá a resposta.
Avisos
- Se a qualquer momento sua soma negativa resultar em um número maior que o divisor, sua estimativa não foi alta o suficiente. Apague todo esse passo e tente estimar maiores.
- Se a qualquer momento sua soma negativa resultar em um negativo número, então sua estimativa foi muito alta. Apague todo esse passo e tente estimar.
Outros recursos
Artigos sobre o tópico "Dividir por um número com dois ou mais dígitos"
Оцените, пожалуйста статью
Similar
Popular