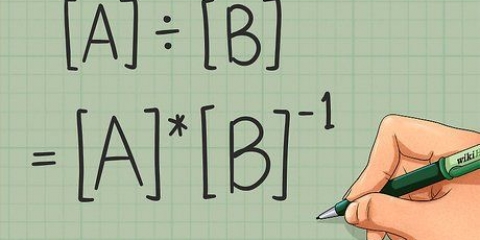Transposição da matriz A = A Primeira coluna de A:
1
2
3 
uma =
1 4 7
2 5 8
3 6 9 
matriz z =
4 7 2 1
3 9 8 6 matriz z =
4 3
7 9
2 8
1 6 
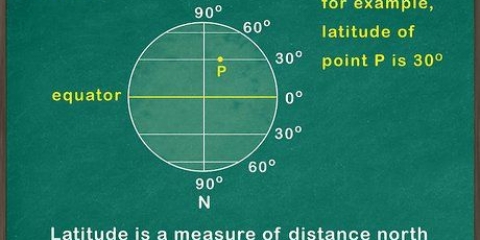
Se a matriz B é uma m X n matriz (m linhas e n colunas), então a matriz transposta B é uma n X m matriz (n linhas e m colunas). Para cada elemento bxy (X-a, y-a coluna) em B, a matriz B tem um elemento igual em byx (y-a fila, X-a coluna). 

Se você não conseguir visualizar isso, desenhe uma matriz 4x4 em um pedaço de papel. Agora dobre sobre a diagonal principal. Você vê como os elementos de um14 e um41 tocar um ao outro? Eles trocam de lugar na transposição, como qualquer outro par que se toca quando dobrado. 


Conjugação complexa de C =
2-eu 3+2eu
0-eu 5-0eu 
Transposição conjugada de C = C =
2-eu 0-eu
3+2eu 5-0eu
Transpor uma matriz
Contente
Uma transposição de matrizes é uma ferramenta matemática útil para entender a estrutura de matrizes. Funções que você já conhece de matrizes, como quadrado e simetria, influenciam os resultados da transposição de maneira óbvia. A transposição também serve para expressar vetores como matrizes, ou calcular os produtos de vetores. Ao lidar com matrizes complexas, o conceito intimamente relacionado de uma transposição conjugada o ajudará com muitos problemas.
Degraus
Parte 1 de 3: Transpondo uma matriz

1. Comece com qualquer matriz. Você pode transpor qualquer matriz independentemente do número de linhas e colunas. Matrizes quadradas, com um número igual de linhas e colunas, são as mais transpostas, então usaremos uma matriz quadrada simples como exemplo:
- matriz uma =
1 2 3
4 5 6
7 8 9

2. Faça da primeira linha da matriz a primeira coluna da transposição. Reescreva a primeira linha da matriz como uma coluna:
1
2
3

3. Repita para as linhas restantes. A segunda linha da matriz original torna-se a segunda coluna da transposição. Repita esse padrão até transformar cada linha em uma coluna:
1 4 7
2 5 8
3 6 9

4. Pratique em uma matriz não quadrada. A transposição é exatamente a mesma para uma matriz não quadrada. Você reescreve a primeira linha como a primeira coluna, a segunda linha como a segunda coluna e assim por diante. Aqui está um exemplo codificado por cores para mostrar onde os elementos terminam:
4 7 2 1
3 9 8 6
4 3
7 9
2 8
1 6

5. Expresse a transposição matematicamente. O conceito é bastante simples, mas é bom poder descrevê-lo em termos matemáticos. Nenhum jargão é necessário fora da notação matricial básica:
Parte 2 de 3: Casos especiais

1. (M = M. A transposição de uma transposição é a matriz original. Isso faz muito sentido, já que você está apenas trocando as linhas e colunas. Trocá-los novamente o levará de volta ao início.

2. Incline as matrizes quadradas sobre a diagonal principal. Em uma matriz quadrada, uma transposição `inclinará` a matriz ao longo da diagonal principal. Em outras palavras, os elementos em uma linha diagonal do elemento a11 no canto inferior direito permanecem os mesmos. Os outros elementos se moverão na diagonal e terminarão na mesma distância da diagonal, no lado oposto.

3. Transpor uma matriz simétrica. Uma matriz simétrica é simétrica em relação à diagonal principal. Se usarmos o `tilt` ou `fold` como descrito acima, podemos ver imediatamente que nada muda. Todos os pares de elementos que trocam de lugar já eram idênticos. Na verdade, esta é a maneira padrão de definir uma matriz simétrica. Se a matriz A = A, então a matriz A é simétrica.
Parte 3 de 3: Transposição conjugada de uma matriz complexa

1. Comece com uma matriz complexa. Matrizes complexas têm elementos com um componente real e imaginário. Embora você possa fazer uma transposição regular dessas matrizes, a maioria dos cálculos práticos são transposições conjugadas.
- Matriz C =
2+eu 3-2eu
0+eu 5+0eu

2. Pegue a conjugação complexa. A conjugação complexa altera o sinal dos componentes imaginários, sem alterar os componentes reais. Execute esta operação para todos os elementos da matriz.
2-eu 3+2eu
0-eu 5-0eu

3. Transponha os resultados. Faça uma conversão comum do resultado. A matriz que você obtém é a transposição conjugada da matriz original.
2-eu 0-eu
3+2eu 5-0eu
Pontas
- Este artigo usa a notação A para denotar a conversão da matriz A. A notação A` ou à significa o mesmo.
- Este artigo refere-se à conversão conjugada da matriz A como A, a notação mais comum em álgebra linear. Os físicos quânticos costumam usar A em vez. A* é outra opção, mas tente evitar isso, pois algumas fontes usarão este símbolo para indicar uma conjugação complexa.
Artigos sobre o tópico "Transpor uma matriz"
Оцените, пожалуйста статью
Popular