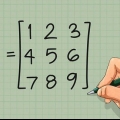Determinando o Determinante de uma Matriz 3x3: 12 Passos (com Imagens)

Contente

Degraus
- Parte 1 de 2: Determinando o determinante
- Parte 2 de 2: Simplificando o problema
Pontas

O determinante de uma matriz é amplamente utilizado em matemática, álgebra linear e geometria superior. Fora do mundo científico, engenheiros e programadores de computação gráfica costumam usar os determinantes das matrizes. Leia este artigo para determinar o determinante de uma matriz 3x3.

Degraus

Parte 1 de 2: Determinando o determinante

Imagem intitulada Encontre o Determinante de uma Matriz 3X3 Passo 1

1. Anote sua matriz 3 x 3. Começamos com uma matriz 3 x 3 A e tentamos o determinante |A| gostar disso. Usamos a seguinte notação geral para a matriz (e esta é a nossa matriz de exemplo):

$m = (\begin{matrix} uma \end{matrix} 11 {uma}_{12} {uma}_{13} {uma}_{21} & {uma}_{22} & {uma}_{23} {uma}_{31} & {uma}_{32} & {uma}_{33}) = (\begin{matrix} 1 & 5 & 3 \\ 2 & 4 & 7 \\ 4 & 6 & 2 \end{matrix})$ $M={begin{pmatrix}a_{{11}}&a_{{12}}&a_{{13}}\a_{{21}}&a_{{22}}&a_{ {23}}\a_{{31}}&a_{{32}}&a_{{33}}end{pmatrix}}={begin{pmatrix}1&5&3\2& 4&7\4&6&2end{pmatrix}}$

Imagem intitulada Encontre o Determinante de uma Matriz 3X3 Passo 2

2. Escolha uma linha ou coluna. Esta será a sua linha ou coluna de referência. Você receberá a mesma resposta, não importa qual você escolha. Agora é só escolher a primeira linha. Mais tarde, vamos aconselhá-lo sobre como escolher a opção mais fácil de calcular.

Vamos escolher a primeira linha da nossa matriz de exemplo A. Circule o 1 5 3. Em termos gerais, circule um₁₁ uma₁₂ uma₁₃.

Imagem intitulada Encontre o Determinante de uma Matriz 3X3 Passo 3

3. Risque a linha e a coluna do primeiro elemento. Olhe para a linha ou coluna que você circulou e selecione o primeiro elemento. Desenhe uma linha através da linha e coluna correspondentes. Se tudo correr bem, isso agora produz quatro números. Tratamos isso como uma matriz 2 x 2.

Em nosso exemplo, a linha de referência é 1 5 3. Isto primeiro elemento está na linha 1 e na coluna 1. Risque a linha 1 e a coluna 1 completamente. Anote os elementos restantes como ummatriz 2 x 2:

~~1 5 3~~
2 4 7
4 6 2

Imagem intitulada Encontre o Determinante de uma Matriz 3X3 Passo 4

4. Determine o determinante da matriz 2 x 2. Não se esqueça: a matriz

(\begin{matrix} uma & b \\ c & d \end{matrix})

${begin{pmatrix}a&b\c&dend{pmatrix}}$ tem um determinante de anúncio - bc. Você sabe disso desenhando uma cruz (X) através da matriz 2 x 2. Multiplique os dois números conectados pelo do X. Em seguida, subtraia o produto dos dois números conectados pelo /. Use esta fórmula para calcular o determinante da matriz que você acabou de encontrar.

No nosso exemplo, o determinante da matriz é

(\begin{matrix} 4 & 7 \\ 6 & 2 \end{matrix})

${begin{pmatrix}4&7\6&2end{pmatrix}}$ = 4 * 2 - 7 * 6 = -34.

Esse determinante é chamado de menor do elemento que escolhemos em nossa matriz original. Neste caso temos o menor de uma₁₁ encontrei.

Imagem intitulada Encontre o Determinante de uma Matriz 3X3 Passo 5

5. Multiplique a resposta pelo elemento escolhido. Lembre-se de que você selecionou um elemento de sua linha (ou coluna) de referência quando decidiu qual linha e coluna riscar. Multiplique este elemento pelo determinante que você acabou de calcular para a matriz 2x2.

No nosso exemplo temos um₁₁ selecionado, que tem um valor de 1. Multiplique isso por -34 (o determinante da matriz 2x2) para obter 1*-34 = -34 para obter.

Imagem intitulada Encontre o Determinante de uma Matriz 3X3 Passo 6

6. Determine o sinal de sua resposta. Agora multiplique a resposta por 1 ou por -1 para obter o cofator do seu elemento escolhido. Qual você usa depende da posição do elemento na matriz 3x3. Memorize a seguinte tabela simples para descobrir qual elemento causa o quê:

+ - +
- + -
+ - +

Porque nós uma₁₁ escolheu, marcado com um +, multiplicamos o número por +1 (ou seja, não fazemos nada com ele). A resposta ainda é -34.

Outra maneira de determinar o sinal é com a fórmula (-1), onde eu e j formar a linha e a coluna do elemento.

Imagem intitulada Encontre o Determinante de uma Matriz 3X3 Passo 7

7. Repita este processo para o segundo elemento em sua linha ou coluna de referência. Continue com a matriz 3x3 original, com a linha ou coluna que você circulou anteriormente. Repita o mesmo processo com este elemento:

Cruze a linha e a coluna desse elemento. Neste caso, você seleciona o elemento a₁₂ (com valor 5). Cruze a primeira linha (1 5 3) e a segunda coluna

(\begin{matrix} 5 \\ 4 \\ 6 \end{matrix})

${begin{pmatrix}5\4\6end{pmatrix}}$ .

Trate os elementos restantes como uma matriz 2x2. No nosso exemplo, a matriz é

(\begin{matrix} 2 & 7 \\ 4 & 2 \end{matrix})

${begin{pmatrix}2&7\4&2end{pmatrix}}$

Determine o determinante desta matriz 2x2. Use a fórmula ad - bc. (2*2 - 7*4 = -24)

Multiplique isso pelo elemento escolhido da matriz 3x3. -24 * 5 = -120

Determine se multiplica por -1. Use a tabela de caracteres ou a fórmula (-1). temos o elemento a₁₂ escolhido, e isso é um – na tabela de caracteres. Precisamos mudar o sinal da nossa resposta: (-1)*(-120) = 120.

Imagem intitulada Encontre o Determinante de uma Matriz 3X3 Passo 8

8. Repita para o terceiro elemento. Agora você tem que encontrar um cofator. Calcule i para o terceiro termo em sua linha ou coluna de referência. Aqui está uma explicação rápida de como calcular o cofator de ₁₃ em nosso exemplo:

Cruze a linha 1 e a coluna 3 e obtenha

(\begin{matrix} 2 & 4 \\ 4 & 6 \end{matrix})

${begin{pmatrix}2&4\4&6end{pmatrix}}$

Seu determinante é 2*6 - 4*4 = -4.

Multiplique isso pelo elemento a₁₃: -4 * 3 = -12.

elemento a₁₃ é um + na tabela de caracteres, então a resposta é -12.

Imagem intitulada Encontre o Determinante de uma Matriz 3X3 Passo 9

9. Adicione os três resultados juntos. Este é o passo final. Você calculou cofatores, um para cada elemento em uma única linha ou coluna. Adicione-os e você encontrou o determinante da matriz 3x3.

No nosso exemplo, o determinante é -34 + 120 + -12 = 74.

Parte 2 de 2: Simplificando o problema

Imagem intitulada Encontre o Determinante de uma Matriz 3X3 Passo 10

1. Escolha a referência com mais zeros. Não se esqueça que você cada pode escolher linha ou coluna como referência. Você receberá a mesma resposta, não importa o que você escolher. Se você escolher uma linha ou coluna com zeros, você só precisa calcular o cofator dos elementos que não são zero. O motivo é o seguinte:

Suponha que você escolha a linha 2, com os elementos a₂₁, uma₂₂, e um₂₃. Para resolver este problema, olhamos para três matrizes 2x2 diferentes. Suponha que chamemos isso de A₂₁, uma₂₂ e A₂₃.
O determinante da matriz 3x3 é um₂₁|A₂₁| - uma₂₂|A₂₂| + um₂₃|A₂₃|.
Se os termos um₂₂ e um₂₃ são ambos 0, então nossa fórmula se torna₂₁|A₂₁| - 0*|A₂₂| + 0*|A₂₃| = um₂₁|A₂₁| - 0 + 0 = um₂₁|A₂₁|. Agora só precisamos calcular o cofator de um único elemento.

Imagem intitulada Encontre o Determinante de uma Matriz 3X3 Passo 11

2. Some as linhas para simplificar a matriz. Se você pegar os valores de uma linha e adicioná-los a outra linha, o determinante da matriz não mudará. O mesmo vale para as colunas. Você pode fazer isso repetidamente - ou multiplicar os valores por uma constante antes de adicionar - para obter o maior número possível de zeros na matriz. Isso pode poupar muito trabalho.

Por exemplo, suponha que você tenha uma matriz 3x3:

(\begin{matrix} 9 & - 1 & 2 \\ 3 & 1 & 0 \\ 7 & 5 & - 2 \end{matrix})

${begin{pmatrix}9&-1&2\3&1&0\7&5&-2end{pmatrix}}$

A cada 9 na posição um₁₁ para se livrar dele, podemos multiplicar a segunda linha por -3 e adicionar o resultado à primeira. A nova primeira linha torna-se então [9 -1 2] + [-9 -3 0] = [0 -4 2].

A nova matriz é

(\begin{matrix} 0 & - 4 & 2 \\ 3 & 1 & 0 \\ 7 & 5 & - 2 \end{matrix})

${begin{pmatrix}0&-4&2\3&1&0\7&5&-2end{pmatrix}}$ Tente usar o mesmo truque para as colunas, para₁₂ para fazer um 0.

Imagem intitulada Encontre o Determinante de uma Matriz 3X3 Passo 12

3. Aprenda o truque para resolver matrizes triangulares. Nesses casos especiais, o determinante é simplesmente o produto dos elementos ao longo da diagonal principal, de um₁₁ superior esquerdo para um₃₃ canto inferior direito. Ainda estamos falando de matrizes 3x3, mas matrizes `triangulares` possuem padrões especiais de valores que não zero são:

Matriz Triângulo Superior: Todos os elementos diferentes de zero estão na diagonal principal ou acima dela. Todos os valores abaixo são zero.

Matriz Triângulo Inferior: Todos os elementos diferentes de zero estão na diagonal principal ou abaixo dela.

Matriz diagonal: Todos os elementos diferentes de zero estão na diagonal principal. (Um subconjunto do acima.)

Pontas

Este método pode ser usado para matrizes quadradas de qualquer tamanho. Por exemplo, se você usar isso para uma matriz 4x4, você mantém após o "descartar" uma matriz 3x3, para a qual você pode calcular o determinante conforme indicado acima. Esteja avisado, porque fazer isso à mão será muito chato!
Se todos os elementos de uma linha ou coluna são iguais a 0, então o determinante dessa matriz é igual a 0.