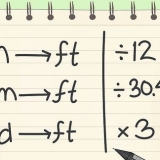Compartilhamento de matrizes

Contente

Se você sabe como multiplicar duas matrizes entre si, então você está no caminho certo para poder `dividir` uma matriz por outra matriz. A divisão está entre aspas porque as matrizes tecnicamente não podem ser divididas. Em vez disso, multiplicamos uma matriz pela inverso de outra matriz. Esses cálculos são frequentemente usados ​​para resolver sistemas de equações lineares.

Degraus

Parte 1 de 3: Entenda que `compartilhar` é impossível

Imagem intitulada Divide Matrices Step 1
1. Entenda o que significa `compartilhar` uma matriz. Tecnicamente não existe divisão matricial. A divisão de matrizes não é uma função definida. O mais próximo disso é multiplicar pela inversa de outra matriz. Em outras palavras, embora [A] ÷ [B] não esteja definido, você pode resolver o problema [A] * [B]. Como essas duas equações são equivalentes a escalares, isso "parece" uma divisão de matrizes, mas é importante usar a terminologia correta.
  • Observe que [A] * [B] e [B] * [A] não são o mesmo problema. Você pode ter que resolver ambos para encontrar todas as respostas possíveis.
  • Por exemplo, em vez de (13263913)÷(7423){displaystyle {begin{pmatrix}13&26\39&13end{pmatrix}}div {begin{pmatrix}7&4\2&3end{pmatrix}}}{begin{pmatrix}13&26\39&13end{pmatrix}}div {begin{pmatrix}7&4\2&3end{pmatrix}}, escrever (13263913)*(7423)-1{displaystyle {begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}7&4\2&3end{pmatrix}}^{-1}}{begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}7&4\2&3end{pmatrix}}^{{-1}}.
    talvez você devesse também (7423)-1*(13263913){displaystyle {begin{pmatrix}7&4\2&3end{pmatrix}}^{-1}*{begin{pmatrix}13&26\39&13end{pmatrix}}}{begin{pmatrix}7&4\2&3end{pmatrix}}^{{-1}}*{begin{pmatrix}13&26\39&13end{pmatrix}} calcular, o que pode gerar apenas uma resposta diferente.
Imagem intitulada Divide Matrices Step 2
2. Verifique se a `matriz divisora` é quadrada é. Para poder determinar a inversa de uma matriz, ela deve ser uma matriz quadrada, portanto, com o mesmo número de linhas e colunas. Se a matriz da qual você deseja encontrar a inversa não for uma matriz quadrada, então não há solução única para o problema.
  • O termo `matriz divisora` é um pouco solto, porque não se trata realmente de um problema de divisão. Para [A] * [B], isso se refere à matriz [B]. No nosso exemplo isso é (7423){displaystyle {begin{pmatrix}7&4\2&3end{pmatrix}}}{begin{pmatrix}7&4\2&3end{pmatrix}}.
  • Uma matriz com uma inversa é chamada `invertível` ou `não singular.` Matrizes sem inversa são `singulares.`
    • Imagem intitulada Divide Matrices Step 3
    3. Verifique se as duas matrizes podem ser multiplicadas. Para multiplicar duas matrizes, o número de colunas da primeira matriz deve ser igual ao número de linhas da segunda matriz. Se isso não funcionar em ambos os casos ([A] * [B] ou [B] * [A]), não há solução para o problema.
  • Por exemplo, se [A] for uma matriz 4 x 3 (4 linhas, 3 colunas) e [B] for uma matriz 2 x 2 (2 linhas, 2 colunas), então não há solução. [A] * [B] não funciona porque 3 ≠ 2, e [B] * [A] não funciona porque 2 ≠ 4.
  • Saiba que a inversa [B] sempre tem o mesmo número de linhas e colunas que a matriz original [B]. Não é necessário calcular o inverso para concluir esta etapa.
  • Em nosso problema de exemplo, ambas as matrizes são 2 x 2, então elas podem ser multiplicadas em qualquer ordem.
    • Imagem intitulada Divide Matrices Step 4
    4. Determine o determinante de uma matriz 2 x 2. Há mais uma verificação necessária antes que você possa determinar a inversa de uma matriz. O determinante da matriz não pode ser zero. Se o determinante é zero, então a matriz não tem inversa. Veja como determinar o determinante no caso mais simples (a matriz 2 x 2):
  • Matriz 2×2: o determinante da matriz (umabcd){displaystyle {begin{pmatrix}a&b\c&dend{pmatrix}}}{begin{pmatrix}a&b\c&dend{pmatrix}} é anúncio - bc. Em outras palavras, pegue o produto da diagonal principal (superior esquerdo para inferior direito) e subtraia o produto da antidiagonal (superior direito para inferior esquerdo) de lá.
  • Por exemplo, a matriz (7423){displaystyle {begin{pmatrix}7&4\2&3end{pmatrix}}}{begin{pmatrix}7&4\2&3end{pmatrix}} tem o determinante (7)(3) - (4)(2) = 21 - 8 = 13. Isso não é zero, então é possível determinar o inverso.
    • Imagem intitulada Divide Matrices Step 5
    5. Determine o determinante de uma matriz maior. Se sua matriz for 3 x 3 ou maior, será necessário mais algum trabalho para determinar o determinante:
  • matriz 3 x 3: Escolha um elemento e cruze a linha e a coluna a que pertence. Determine o determinante da matriz 2 x 2 restante, multiplique pelo elemento escolhido e mantenha uma tabela de sinais da matriz para determinar o sinal. Repita para os outros dois elementos na mesma linha e coluna do primeiro que você escolheu e, em seguida, adicione todos os três determinantes. Leia este artigo para obter instruções passo a passo e dicas para fazer isso mais rápido.
  • Matrizes maiores: O uso de uma calculadora gráfica ou software é recomendado aqui. O método é semelhante ao de uma matriz 3 x 3, mas leva muito tempo se você fizer isso manualmente. Por exemplo, para encontrar o determinante de uma matriz 4 x 4, você deve primeiro encontrar os determinantes de quatro matrizes 3 x 3.
    • Imagem intitulada Divide Matrices Step 6
    6. Continuar. Se sua matriz não for um quadrado, ou se seu determinante for zero, escreva-o como `sem solução única`. O problema está resolvido. Se a matriz for um quadrado e seu determinante não for zero, pule para a próxima parte para o próximo passo: encontrar a inversa.

    Parte 2 de 3: Invertendo a matriz

    Imagem intitulada Divide Matrices Step 7
    1. Troque as posições dos elementos da diagonal principal 2 x 2. Se você estiver lidando com uma matriz 2 x 2, você pode usar um atalho para tornar esse cálculo muito mais fácil. A primeira etapa desta solução rápida envolve a troca do elemento superior esquerdo pelo elemento inferior direito. Por exemplo:
    • (7423){displaystyle {begin{pmatrix}7&4\2&3end{pmatrix}}}{begin{pmatrix}7&4\2&3end{pmatrix}} → (3427){displaystyle {begin{pmatrix}3&4\2&7end{pmatrix}}}{begin{pmatrix}3&4\2&7end{pmatrix}}
    • Observação: A maioria das pessoas usa uma calculadora para determinar a inversa de uma matriz 3 x 3 (ou maior). Se você ainda quiser calcular isso manualmente, veja o final desta parte.
    Imagem intitulada Divide Matrices Step 8
    2. Pegue o oposto dos outros dois elementos, mas deixe-os nessa posição. Em outras palavras, multiplique o topo juiz e inferior deixou-elementos com-1:
  • (3427){displaystyle {begin{pmatrix}3&4\2&7end{pmatrix}}}{begin{pmatrix}3&4\2&7end{pmatrix}} → (3-4-27){displaystyle {begin{pmatrix}3&-4\-2&7end{pmatrix}}}{begin{pmatrix}3&-4\-2&7end{pmatrix}}
    • Imagem intitulada Divide Matrices Step 9
    3. Pegue o inverso do determinante. Você encontrou o determinante desta matriz na seção acima, então não há necessidade de calculá-lo novamente. Basta escrever o recíproco de 1/(determinante):
  • No nosso exemplo, o determinante é 13. A recíproca disso é 113{displaystyle {frac {1}{13}}}{frac{1}{13}}.
    • Imagem intitulada Divide Matrices Step 10
    4. Multiplique a nova matriz pelo inverso do determinante. Multiplique cada elemento da nova matriz pelo recíproco que você acabou de encontrar. A matriz resultante é a inversa da matriz 2 x 2:
  • 113*(3-4-27){displaystyle {frac {1}{13}}*{begin{pmatrix}3&-4\-2&7end{pmatrix}}}{frac{1}{13}}*{begin{pmatrix}3&-4\-2&7end{pmatrix}}
    =(313-413-213713){displaystyle {begin{pmatrix}{frac {3}{13}}&{frac {-4}{13}}\{frac {-2}{13}}&{frac {7}{13}}end{pmatrix}}}{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}}\{frac{-2}{13}}&{frac{7} {13}}end{pmatrix}}
    • Imagem intitulada Divide Matrices Step 11
    5. Confirme se a inversa está correta. Para verificar seu trabalho, multiplique a inversa pela matriz original. Se a inversa estiver correta, então seu produto é sempre a identidade da matriz, (1001){displaystyle {begin{pmatrix}1&0\0&1end{pmatrix}}}{begin{pmatrix}1&0\0&1end{pmatrix}} Se estiver matematicamente correto, continue para a próxima seção para concluir a elaboração do problema.
  • Para o propósito do problema de exemplo, multiplicamos (313-413-213713)*(7423)=(1001){displaystyle {begin{pmatrix}{frac {3}{13}}&{frac {-4}{13}}\{frac {-2}{13}}&{frac {7}{13}}end{pmatrix}}*{begin{pmatrix}7&4\2&3end{pmatrix}}={begin{pmatrix}1&0\0&1end{pmatrix}}}{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}}\{frac{-2}{13}}&{frac{7} {13}}end{pmatrix}}*{begin{pmatrix}7&4\2&3end{pmatrix}}={begin{pmatrix}1&0\0&1end{pmatrix} }}.
  • Veja o wikihow para mais informações sobre multiplicação de matrizes.
  • Nota: A multiplicação de matrizes não é comutativa: a ordem dos fatores é importante. Ao multiplicar uma matriz pela sua inversa, ambas resultarão na matriz identidade.
    • Imagem intitulada Divide Matrices Step 12
    6.Determine a inversão de matriz de uma matriz 3 x 3 ou maior. A menos que você seja novo neste processo, você pode economizar muito tempo usando uma calculadora gráfica ou software de matemática em matrizes maiores. Se você precisar calculá-lo manualmente, aqui está um resumo rápido de um método que você pode usar:
  • Adicione a matriz identidade I ao lado direito da sua matriz. Por exemplo, [B] → [B | EU ]. A matriz identidade tem elementos `1` ao longo da diagonal principal e elementos `0` em todas as outras posições.
  • Faça operações de linha para reduzir a matriz até que o lado esquerdo esteja na forma escalonada de linha, então continue reduzindo até que o lado esquerdo seja a matriz identidade.
  • Quando toda a operação estiver concluída, sua matriz estará no formato [I | B]. Em outras palavras, o lado direito se torna o inverso da matriz original.

    • Parte 3 de 3: Multiplique as matrizes para completar o problema

    Imagem intitulada Divide Matrices Step 13
    1. Escreva as duas equações possíveis. Na "matemática comum" com escalares, a multiplicação é comutativa; 2 x 6 = 6 x 2. Isso não se aplica a matrizes, então você pode ter que resolver dois problemas:
    • [A] * [B] é a solução X por problema X[B] = [A].
    • [B] * [A] é a solução X para o problema [B]X = [A].
    • Se isso for parte de uma equação, certifique-se de aplicar a mesma operação em ambos os lados da equação. Se [A] = [C], então [B][A] é não igual a [C][B], porque [B] está à esquerda de [A], mas à direita de [C].
    Imagem intitulada Divide Matrices Step 14
    2. Determine as dimensões da sua resposta. As dimensões da matriz final são as dimensões externas dos dois fatores. Tem o mesmo número de linhas que a primeira matriz e o mesmo número de colunas que a segunda matriz.
  • Voltando ao exemplo original: ambos (13263913){displaystyle {begin{pmatrix}13&26\39&13end{pmatrix}}}{begin{pmatrix}13&26\39&13end{pmatrix}} e (313-413-213713){displaystyle {begin{pmatrix}{frac {3}{13}}&{frac {-4}{13}}\{frac {-2}{13}}&{frac {7}{13}}end{pmatrix}}}{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}}\{frac{-2}{13}}&{frac{7} {13}}end{pmatrix}} são matrizes 2 x 2, então as dimensões da resposta também são 2 x 2.
  • Para dar um exemplo um pouco mais complicado: se [A] é um 4 x é uma matriz 3 e [B] é uma matriz 3 x 3 matriz, então a matriz [A] * [B] tem dimensões 4 x 3.
    • Imagem intitulada Divide Matrices Step 15
    3. Determine o valor do primeiro elemento. Confira o artigo vinculado para obter instruções detalhadas ou atualize seu conhecimento com este resumo:
  • Para encontrar a linha 1, coluna 1 de [A][B], encontre o produto escalar de [A] linha 1 e [B] coluna 1. Então, para uma matriz 2 x 2, você calcula uma1,1*b1,1+uma1,2*b2,1{displaystyle a_{1,1}*b_{1,1}+a_{1,2}*b_{2,1}}a_{{1,1}}*b_{{1,1}}+a_{{1,2}}*b_{{2,1}}.
  • Em nosso exemplo (13263913)*(313-413-213713){displaystyle {begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}{frac {3}{13}}&{frac {-4}{13}}\{frac {-2}{13}}&{frac {7}{13}}end{pmatrix}}}{begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}} \{frac{-2}{13}}&{frac{7}{13}}end{pmatrix}}, é a linha 1 coluna 1 da sua resposta:
    (13*313)+(26*-213){displaystyle (13*{frac {3}{13}})+(26*{frac {-2}{13}})}(13*{frac{3}{13}})+(26*{frac{-2}{13}})
    =3+-4{displaystyle =3+-4}=3+-4
    =-1{estilo de exibição =-1}=-1
    • Imagem intitulada Divide Matrices Step 16
    4. Calcule o produto escalar para cada posição em sua matriz. Por exemplo, o elemento na posição 2.1 é o produto escalar de [A] linha 2 e [B] coluna 1. Tente resolver o exemplo você mesmo. Você deve obter as seguintes respostas:
  • (13263913)*(313-413-213713)=(-1107-5){displaystyle {begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}{frac {3}{13}}&{frac {-4}{13}}\{frac {-2}{13}}&{frac {7}{13}}end{pmatrix}}={begin{pmatrix}-1&10\7&-5end{pmatrix}}}{begin{pmatrix}13&26\39&13end{pmatrix}}*{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}} \{frac{-2}{13}}&{frac{7}{13}}end{pmatrix}}={begin{pmatrix}-1&10\7&-5end {pmatrix}}
  • E a outra solução: (313-413-213713)*(13263913)=(-92193){displaystyle {begin{pmatrix}{frac {3}{13}}&{frac {-4}{13}}\{frac {-2}{13}}&{frac {7}{13}}end{pmatrix}}*{begin{pmatrix}13&26\39&13end{pmatrix}}={begin{pmatrix}-9&2\19&3end{pmatrix}}}{begin{pmatrix}{frac{3}{13}}&{frac{-4}{13}}\{frac{-2}{13}}&{frac{7} {13}}end{pmatrix}}*{begin{pmatrix}13&26\39&13end{pmatrix}}={begin{pmatrix}-9&2\19&3end{ pmmatrix}}

    • Pontas

    • Você pode dividir uma matriz por um escalar, dividindo cada elemento da matriz pelo escalar.
    • Por exemplo, a matriz (6824){displaystyle {begin{pmatrix}6&8\2&4end{pmatrix}}}{begin{pmatrix}6&8\2&4end{pmatrix}} dividido por 2 = (3412){displaystyle {begin{pmatrix}3&4\1&2end{pmatrix}}}{begin{pmatrix}3&4\1&2end{pmatrix}}

    Avisos

    • As calculadoras nem sempre são 100% precisas na matemática matricial. Por exemplo, se sua calculadora indicar que um elemento tem um valor muito pequeno (por exemplo,. 2E), então o valor é provavelmente zero.

    Pr.FaqCartx.info / Educação e comunicação
    Оцените, пожалуйста статью
    Novo
    Tratando o eczema ao redor dos olhos
    Tratando o eczema ao redor dos olhos
    Converter pés quadrados para pés cúbicos
    Converter pés quadrados para pés cúbicos
    Escreva um cartão postal
    Escreva um cartão postal
    Sapato sperry com cadarço
    Sapato sperry com cadarço
    Alimentando veados
    Alimentando veados
    Hackear um site com código html simples
    Hackear um site com código html simples