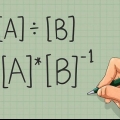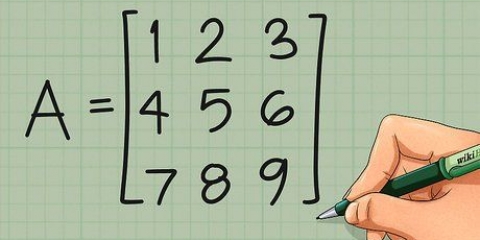Se você tiver mais variáveis, apenas continue a linha o tempo que for necessário. Por exemplo, se você estivesse tentando resolver um sistema de seis variáveis, sua forma padrão seria Au+Bv+Cw+Dx+Ey+Fz=G. Neste artigo vamos focar em sistemas com apenas três variáveis. Resolver um sistema maior é exatamente o mesmo, mas leva mais tempo e mais etapas. Observe que na forma padrão as operações entre os termos são sempre uma adição. Se houver uma subtração em sua equação, em vez de uma adição, você terá que trabalhar com isso mais tarde, tornando seu coeficiente negativo. Para tornar isso mais fácil de lembrar, você pode reescrever a equação e adicionar a operação e tornar o coeficiente negativo. Por exemplo, você pode reescrever a equação 3x-2y+4z=1 como 3x+(-2y)+4z=1. 
Suponha que você tenha um sistema que consiste nas três equações 3x+y-z=9, 2x-2y+z=-3 e x+y+z=7. A linha superior da sua matriz conterá os números 3, 1, -1, 9, pois esses são os coeficientes e a solução da primeira equação. Observe que qualquer variável que não tenha um coeficiente é assumida como tendo um coeficiente de 1. A segunda linha da matriz torna-se 2, -2, 1, -3 e a terceira linha 1, 1, 1, 7. Certifique-se de alinhar os coeficientes x na primeira coluna, os coeficientes y na segunda, os coeficientes z na terceira e os termos de solução na quarta. Quando você terminar de trabalhar com a matriz, essas colunas serão importantes ao escrever sua solução. 

Você pode indicar qualquer posição específica em uma matriz usando uma combinação de R e C. Por exemplo, para denotar um termo na segunda linha, terceira coluna, você poderia chamá-lo de R2C3. 

É comum usar frações na multiplicação escalar porque muitas vezes você deseja obter uma linha diagonal de 1s. Acostume-se a trabalhar com frações. Também será mais fácil (para a maioria das etapas na resolução da matriz) poder escrever suas frações na forma imprópria e convertê-las novamente em números mistos para a solução final. É por isso que o número 1 2/3 é mais fácil de trabalhar se você escrevê-lo como 5/3. Por exemplo, a primeira linha (R1) do nosso problema de exemplo começa com os termos [3.1,-1,9]. A matriz de solução deve conter um 1 na primeira posição da primeira linha. Para `transformar` o 3 em 1, podemos multiplicar a linha inteira por 1/3. Isso cria o novo R1 de [1.1/3,-1/3.3]. Certifique-se de deixar quaisquer sinais negativos onde eles pertencem. 
Você pode usar a notação abreviada e declarar esta operação como R2-R1=[0,-1,2,6]. Lembre-se que adição e subtração são apenas formas opostas da mesma operação. Você pode pensar nisso como adicionar dois números ou subtrair o oposto. Por exemplo, se você começar com a equação simples 3-3=0, você pode pensar nisso como um problema de adição de 3+(-3)=0. O resultado é o mesmo. Isso parece simples, mas às vezes é mais fácil considerar um problema de uma forma ou de outra. Apenas fique de olho em seus sinais negativos. 
Casal; que existe uma linha 1 de [1,1,2,6] e uma linha 2 de [2,3,1,1]. Você quer um termo 0 na primeira coluna de R2. Ou seja, você quer mudar o 2 para um 0. Para fazer isso, você precisa subtrair um 2. Você pode obter um 2 multiplicando primeiro a linha 1 pela multiplicação escalar 2 e, em seguida, subtraindo a primeira linha da segunda linha. Em forma abreviada, isso pode ser escrito como R2-2*R1. Primeiro multiplique R1 por 2 para obter [2,2,4,12]. Então subtraia isso de R2 para obter [(2-2),(3-2),(1-4),(1-12)]. Simplifique isso e seu novo R2 se torna [0,1,-3,-11]. 
Um erro comum ocorre ao executar uma etapa combinada de multiplicação e adição em um movimento. Por exemplo, suponha que você precise subtrair R1 de R2 duas vezes. Quando você multiplica R1 por 2 para fazer este passo, lembre-se que R1 não muda na matriz. Você só faz a multiplicação para mudar R2. Copie R1 em sua forma original primeiro e depois faça a alteração para R2. 
1. Faça um 1 na primeira linha, primeira coluna (R1C1). 2. Faça um 0 na segunda linha, primeira coluna (R2C1). 3. Faça um 1 na segunda linha, segunda coluna (R2C2). 4. Faça um 0 na terceira linha, primeira coluna (R3C1). 5. Faça um 0 na terceira linha, segunda coluna (R3C2). 6. Faça um 1 na terceira linha, terceira coluna (R3C3). 
Crie um 0 na segunda linha, terceira coluna (R2C3). Crie um 0 na primeira linha, terceira coluna (R1C3). Crie um 0 na primeira linha, segunda coluna (R1C2). 


Observe que a multiplicação e a divisão são apenas funções inversas uma da outra. Podemos dizer que multiplicamos por 1/3 ou dividimos por 3, sem alterar o resultado. 
Escreva a linha 3 (que não mudou) se R3=[1,1,1,7]. Tenha cuidado ao subtrair números negativos para garantir que os caracteres permaneçam corretos. Agora primeiro vamos colocar as frações em sua forma imprópria. Isso facilita as etapas posteriores da solução. Você pode simplificar as frações na última etapa do problema. 
Observe que, se a metade esquerda da sequência começar a ficar parecida com a solução com 0 e 1, a metade direita pode ficar feia, com frações impróprias. Basta deixá-los para o que eles são agora. Lembre-se de continuar copiando as linhas não afetadas, então R1=[1,1/3,-1/3,3] e R3=[1,1,1,7]. 
Continue copiando ao longo de R1=[1.1/3,-1/3.3] e R2=[0.1,-5/8.27/8]. Lembre-se de que você altera apenas uma linha de cada vez. 

Observe que as frações que pareciam bastante complicadas no passo anterior já estão começando a resolver. Continue com R1=[1.1/3,-1/3.3] e R2=[0.1,-5/8.27/8]. Observe que neste ponto você tem a diagonal de 1 para sua matriz de solução. Você só precisa converter três elementos da matriz em 0s para encontrar sua solução. 
Então pegue R1=[1,1/3,-1/3,3] e R3=[0,0,1,1]. 
Pegue o inalterado R2=[0,1,0,4] e R3=[0,0,1,1]. 

1002 0104 0011 


Como cada equação simplifica para uma afirmação matemática verdadeira, suas soluções estão corretas. Se alguma das soluções não estiver correta, verifique seu trabalho novamente e procure por erros. Alguns erros comuns ocorrem ao se livrar de sinais de menos ao longo do caminho ou ao confundir a multiplicação e adição de frações. 
Resolver matrizes
Contente
Uma matriz é uma maneira muito útil de representar números em formato de bloco, que você pode usar para resolver um sistema de equações lineares. Se você tiver apenas duas variáveis, provavelmente usará um método diferente. Leia sobre isso em Resolvendo um sistema de equações para exemplos desses outros métodos. Mas se você tem três ou mais variáveis, uma matriz é o ideal. Usando combinações repetidas de multiplicação e adição, você pode chegar sistematicamente a uma solução.
Degraus
Parte 1 de 4: Elaborando a matriz

1. Verifique se você tem dados suficientes. Para obter uma solução única para cada variável em um sistema linear usando uma matriz, você deve ter tantas equações quanto o número de variáveis que está tentando resolver. Por exemplo: com as variáveis x, yez você precisa de três equações. Se você tem quatro variáveis, você precisa de quatro equações.
- Se você tiver menos equações do que o número de variáveis, aprenderá alguns limites das variáveis (como x = 3y e y = 2z), mas não poderá obter uma solução precisa. Para este artigo, trabalharemos apenas para uma solução única.

2. Escreva suas equações na forma padrão. Antes que você possa despejar os dados das equações em uma forma de matriz, você primeiro escreve cada equação na forma padrão. A forma padrão para uma equação linear é Ax+By+Cz=D, onde as letras maiúsculas são os coeficientes (números) e o último número (neste exemplo, o D) está à direita do sinal de igual.

3. Coloque os números do sistema de equações em uma matriz. Uma matriz é um grupo de números, dispostos em uma espécie de tabela, com os quais trabalharemos para resolver o sistema. Ele basicamente contém os mesmos dados que as próprias equações, mas em um formato mais simples. Para fazer a matriz de suas equações na forma padrão, basta copiar os coeficientes e o resultado de cada equação em uma única linha e empilhar essas linhas umas sobre as outras.

4. Desenhe um grande colchete ao redor de toda a sua matriz. Por convenção, uma matriz é denotada por um par de colchetes, [ ], ao redor de todo o bloco de números. Os parênteses não afetam a solução de forma alguma, mas indicam que você está trabalhando com matrizes. Uma matriz pode consistir em qualquer número de linhas e colunas. Neste artigo, usaremos parênteses em torno de uma linha de termos para indicar que eles pertencem um ao outro.

5. Uso de simbolismo comum. Ao trabalhar com matrizes é comum referir-se às linhas com a abreviatura R e as colunas com a abreviatura C. Você pode usar números junto com essas letras para designar uma linha ou coluna específica. Por exemplo, para indicar a linha 1 de uma matriz, você pode escrever R1. A linha 2 torna-se então R2.
Parte 2 de 4: Aprendendo as operações para resolver um sistema com uma matriz

1. Entendendo a forma da matriz de solução. Antes de começar a resolver seu sistema de equações, você precisa entender o que vai fazer com a matriz. Neste ponto, você tem uma matriz que se parece com isso:
- 31-19
- 2-21-3
- 1117
- Você trabalha com várias operações básicas para criar a `matriz de solução`. A matriz de solução ficará assim:
- 100x
- 010 anos
- 001z
- Observe que a matriz consiste em 1`s em uma linha diagonal com 0`s em todos os outros espaços, exceto na quarta coluna. Os números na quarta coluna são as soluções para as variáveis x, y e z.

2. Usar multiplicação escalar. A primeira ferramenta à sua disposição para resolver um sistema usando uma matriz é a multiplicação escalar. Este é simplesmente um termo que significa que você multiplica os elementos em uma linha da matriz por um número constante (não uma variável). Ao usar a multiplicação escalar, lembre-se de que você deve multiplicar cada termo de toda a sequência por qualquer número selecionado. Se você esquecer o primeiro termo e apenas multiplicar, obterá uma solução errada. No entanto, você não precisa multiplicar toda a matriz ao mesmo tempo. Com a multiplicação escalar você só trabalha em uma linha de cada vez.

3. Usar adição de linha ou subtração de linha. A segunda ferramenta que você pode usar é adicionar ou subtrair duas linhas da matriz. Para criar os termos 0 em sua matriz de solução, você precisa adicionar ou subtrair números para chegar ao 0. Por exemplo, se R1 de uma matriz for [1,4,3,2] e R2 for [1,3,5,8], então você pode subtrair a primeira linha da segunda linha e criar uma nova linha [ 0,-1, 2,6], porque 1-1=0 (primeira coluna), 3-4=-1 (segunda coluna), 5-3=2 (terceira coluna) e 8-2=6 (quarta coluna). Ao realizar uma adição ou subtração de linha, reescreva seu novo resultado em vez da linha com a qual você começou. Neste caso, retiraríamos a linha 2 e inseriríamos a nova linha [0,-1,2,6].

4. Combine adição de linhas e multiplicação escalar em uma única etapa. Você não pode esperar que os termos sempre correspondam, então pode usar uma simples adição ou subtração para criar zeros em sua matriz. Mais frequentemente, você terá que adicionar (ou subtrair) um múltiplo de outra linha. Para fazer isso, faça a multiplicação escalar primeiro e adicione esse resultado à linha de destino que você está tentando alterar.

5. Copie as linhas que permanecem inalteradas enquanto você trabalha. Ao trabalhar na matriz, você alterará uma única linha de cada vez, seja por multiplicação escalar, adição de linhas ou subtração de linhas, ou por uma combinação de etapas. Ao alterar uma linha, certifique-se de copiar as outras linhas de sua matriz em sua forma original.

6. Trabalhe de cima para baixo primeiro. Para resolver o sistema, você trabalha em um padrão muito organizado, essencialmente "resolvendo" um termo da matriz por vez. A ordem para um array de três variáveis será assim:

7. Trabalhe de baixo para cima. Neste ponto, se você executou as etapas corretamente, está na metade da solução. Você deve ter a linha diagonal de 1`s, com 0`s abaixo dela. Os números na quarta coluna não importam neste momento. Agora você trabalha de volta da seguinte forma:

8. Verifique se você criou a matriz de solução. Se o seu trabalho estiver correto, você criou a matriz de solução com 1`s em uma linha diagonal de R1C1, R2C2, R3C3 e 0`s nas outras posições das três primeiras colunas. Os números na quarta coluna são as soluções para o seu sistema linear.
Parte 3 de 4: Juntando as etapas para resolver o sistema

1. Comece com um exemplo de sistema de equações lineares. Para praticar essas etapas, vamos começar com o sistema que usamos anteriormente: 3x+y-z=9, 2x-2y+z=-3 e x+y+z=7. Se você escrever isso em uma matriz, você terá R1= [3.1,-1,9], R2=[2,-2,1,-3] e R3=[1,1,1,7].

2. Crie um 1 na primeira posição R1C1. Observe que R1 atualmente começa com um 3. Você tem que mudar para 1. Você pode fazer isso por multiplicação escalar, multiplicando todos os quatro termos de R1 por 1/3. Em abreviação, você pode escrever como R1 * 1/3. Isso dá um novo resultado para R1 se R1=[1,1/3,-1/3,3]. Adote R2 e R2, inalterados, se R2=[2,-2,1,-3] e R3=[1,1,1,7].

3. Crie um 0 na segunda linha, primeira coluna (R2C1). Neste ponto R2=[2,-2,1,-3]. Para se aproximar da matriz de solução, você precisa alterar o primeiro termo de 2 para 0. Você pode fazer isso subtraindo duas vezes o valor de R1, já que R1 começa com 1. Em resumo, a operação é R2-2*R1. Lembre-se de que você não altera R1, apenas trabalhe com ele. Então, primeiro copie R1 se R1=[1,1/3,-1/3,3]. Se você dobrar cada termo de R1, obterá 2*R1=[2,2/3,-2/3,6]. Finalmente, subtraia este resultado do R2 original para obter seu novo R2. Trabalhando termo a termo, essa subtração se torna (2-2), (-2-2/3), (1-(-2/3), (-3-6). Simplificamos isso para o novo R2=[0,-8/3,5/3,-9]. Observe que o primeiro termo é 0 (seja qual for o seu objetivo).

4. Crie um 1 na segunda linha, segunda coluna (R2C2). Para continuar formando a linha diagonal de 1, você precisa converter o segundo termo -8/3 em 1. Faça isso multiplicando a linha inteira pelo inverso desse número (-3/8). Simbolicamente, esta etapa é R2*(-3/8). A segunda linha resultante é R2=[0.1,-5/8.27/8].

5. Crie um 0 na terceira linha, primeira coluna (R3C1). Seu foco agora se move para a terceira linha, R3=[1,1,1,7]. Para fazer um 0 na primeira posição, você precisa subtrair um 1 do 1 atualmente nessa posição. Se você olhar para cima, há um 1 na primeira posição de R1. Então você só precisa subtrair R1 de R3 para obter o resultado que você precisa. Trabalhando termo por termo, isso se torna (1-1), (1-1/3), (1-(-1/3)), (7-3). Esses quatro miniproblemas podem ser simplificados para o novo R3=[0.2/3.4/3.4].

6. Faça um 0 na terceira linha, segunda coluna (R3C2). Este valor é atualmente 2/3, mas deve ser convertido para 0. À primeira vista, parece que você pode fazer uma subtração dupla dos valores de R1, já que a coluna correspondente de R1 contém 1/3. Porém, se você dobrar e subtrair todos os valores de R1, o 0 na primeira coluna de R3 muda, o que você não quer. Isso seria um passo para trás em sua solução. Então você tem que trabalhar com alguma combinação de R2. Se você subtrair 2/3 de R2, você cria um 0 na segunda coluna, sem alterar a primeira coluna. Em forma abreviada, é R3- 2/3*R2. Os termos individuais se tornam (0-0), (2/3-2/3), (4/3-(-5/3*2/3)), (4-27/8*2/3). A simplificação então dá R3=[0,0,42/24.42/24].

7. Crie um 1 na terceira linha, terceira coluna (R3C3). Esta é uma multiplicação simples com o inverso do número que diz. O valor atual é 42/24, então você pode multiplicar por 24/42 para obter o valor desejado de 1. Observe que os dois primeiros termos são ambos 0, então qualquer multiplicação permanece 0. O novo valor de R3=[0,0,1,1].

8. Crie um 0 na segunda linha, terceira coluna. R2 é atualmente [0,1,-5/8,27/8], com um valor de -5/8 na terceira coluna. Você tem que transformá-lo para um 0. Isso significa que você tem que realizar alguma operação com R3 que consiste em adicionar 5/8. Como a terceira coluna correspondente de R3 é 1, você precisa multiplicar todos os valores de R3 por 5/8 e adicionar o resultado a R2. Resumindo, isso é R2+5/8*R3. Termo por termo isto é R2=(0+0), (1+0), (-5/8+5/8), (27/8+5/8). Isso pode ser simplificado para R2=[0,1,0,4].

9. Crie um 0 na primeira linha, terceira coluna (R1C3). A primeira linha é atualmente R1=[1.1/3,-1/3.3]. Você tem que converter o -1/3 na terceira coluna para um 0, usando alguma combinação de R3. Você não quer usar R2, porque o 1 na segunda coluna de R2 modificaria o R1 da maneira errada. Então você multiplica R3*1/3 e adiciona o resultado a R1. A notação para isso é R1+1/3*R3. Calcular termo por termo resulta em R1=(1+0), (1/3+0), (-1/3+1/3), (3+1/3). Você pode simplificar isso para um novo R1=[1,1/3,0,10/3].

10. Faça um 0 na primeira linha, segunda coluna (R1C2). Se tudo for bem feito, este deve ser o último passo. Você precisa converter o 1/3 na segunda coluna para um 0. Você pode obter isso multiplicando e subtraindo R2 * 1/3. Resumindo, isso é R1-1/3*R2. O resultado é R1=(1-0), (1/3-1/3), (0-0), (10/3-4/3). Simplificando então dá R1=[1,0,0,2].

11. Procure a matriz de solução. Neste ponto, se tudo correu bem, você teria as três linhas R1=[1,0,0,2], R2=[0,1,0,4] e R3=[0,0,1,1] tem que ter. Observe que se você escrever isso na forma de matriz de blocos com as linhas uma em cima da outra, você terá 1s na diagonal com 0s mais adiante e suas soluções estarão na quarta coluna. A matriz de solução deve ficar assim:

12. Entendendo sua solução. Depois de converter as equações lineares em uma matriz, coloque os coeficientes x na primeira coluna, os coeficientes y na segunda coluna, os coeficientes z na terceira coluna. Se agora você quiser reescrever a matriz em equações, essas três linhas da matriz na verdade significam as três equações 1x+0y+0z=2, 0x+1y+0z=4 e 0x+0y+1z=1. Como podemos riscar os termos 0 e não ter que escrever os coeficientes 1, essas três equações simplificam para a solução, x=2, y=4 e z=1. Esta é a solução para o seu sistema de equações lineares.
Parte 4 de 4: Verificando sua solução

1. Processe as soluções em cada variável em cada equação. É sempre uma boa ideia verificar se sua solução está realmente correta. Você faz isso testando seus resultados nas equações originais.
- As equações originais para este problema eram: 3x+y-z=9, 2x-2y+z=-3, e x+y+z=7. Ao substituir as variáveis pelos valores encontrados, você obtém 3*2+4-1=9, 2*2-2*4+1=-3 e 2+4+1=7.

2. Simplifique qualquer equação. Execute as operações em cada equação de acordo com as regras básicas de operações. A primeira equação simplifica para 6+4-1=9, ou 9=9. A segunda equação pode ser simplificada para 4-8+1=-3, ou -3=-3. A última equação é simplesmente 7 = 7.

3. Escreva suas soluções finais. Para este dado problema a solução final é x=2, y=4 e z=1.
Pontas
- Se o seu sistema de equações for muito complexo, com muitas variáveis, você pode usar uma calculadora gráfica em vez de fazer o trabalho manualmente. Para obter informações sobre isso, você também pode consultar o wikiHow.
Artigos sobre o tópico "Resolver matrizes"
Оцените, пожалуйста статью
Popular