2 x 2 x 3 x 5 x 7 = 420.
O LCF de 20 e 42 é 420.


8 x 1 = 8
8 x 2 = 16
8 x 3 = 24 
O LCF de 5 e 8 é 40. Este é o mínimo múltiplo comum porque é o primeiro fator de ocorrência do mesmo múltiplo para 5 e 8 e, portanto, o LCF para esses números.



18/2 = 9, então escreva 9 em 18. 12/2 = 6, então escreva 6 em 12. 30/2 = 15, então escreva 15 sob 30. 
Fator 3 desses números. 3 é o menor fator primo aqui, o menor número primo divisível por ambos os números.
Divida os três números por 3 e escreva o resultado abaixo desses números.
9/3 = 3, então você escreve um 3 sob 9; 6/3 = 2, então você escreve um 2 sob 6; 15/3 = 5 então você escreve 5 em 15.

Como exemplo, suponha que os números inferiores sejam 2, 39 e 122, então divida 2 e 122 por 2, resultando em uma nova linha inferior: 1, 39 e 61. 
O LCF de 18, 12 e 30 é 180.

Em seguida, divida o segundo número (45) pelo restante (30). 45/30 = 1 (restante 15). Então 45 = 1 x 30 + 15.
Em seguida, divida o restante da primeira etapa (30) pelo restante da segunda etapa (15). 30/15 = 2 (residual 0). Então 30 = 2 x 15 + 0.
O GGD de 210 e 45 é 15.
Você sempre pode usar esse método para encontrar o GGD - basta parar de compartilhar quando chegar a um restante de 0. 


Encontre o mínimo múltiplo comum de dois números
Contente
O mínimo múltiplo comum (KGB) de um grupo de números é o menor número que é um múltiplo de todos os números do grupo. Por exemplo, o LCF de 16 e 20 é 80; 80 é o menor número que é múltiplo de 16 e múltiplo de 20. Você pode encontrar o LCF de dois ou mais números, usando métodos diferentes. Se você quiser saber como encontrar o LCF de dois ou mais números, siga estas etapas.
Degraus
Método 1 de 4: fatoração primária

1. Determine os fatores primos de ambos os números. Este é um método ideal para números maiores. O primeiro passo para encontrar o mínimo múltiplo comum de dois números usando este método é a fatoração de ambos os números para os números primos multiplicados para obter esse número como um produto. Você pode começar fazendo uma lista de dois números (fatores) multiplicados para produzir esse número e depois fatorá-los em seus fatores primos. Suponha que você queira encontrar o mínimo múltiplo comum de 20 e 42. Veja como fatorar. 20 = 2 x 2 x 542 = 2 x 3 x 7

2. Anote qual número primo ocorre com mais frequência nos fatores primos de cada número. Aqui está uma lista de números que ocorrem com mais frequência para cada número primo no exemplo anterior 2 → 2 vezes3 → 1 vez5 → 1 vez7 → 1 vez
3. Multiplique todos os fatores juntos . Aqui está o que você precisa fazer para encontrar o ECG do exemplo:


Método 2 de 4: Liste todos os múltiplos de ambos os números

1. Liste alguns múltiplos do primeiro número em ordem crescente. Este é um método ideal para números menores, especialmente para números menores que 10. Para números maiores, isso não é recomendado, pois pode ser complicado. Suponha que você queira encontrar o KGV de 5 e8. Você primeiro faz uma lista dos múltiplos de 55 x 1 = 55 x 2 = 105 x 3 = 15

2. Agora liste alguns múltiplos do segundo número (8), em ordem crescente.
8 x 2 = 16
8 x 3 = 24

3. Experimente várias possibilidades para ambos os números, até encontrar o mínimo múltiplo comum. Em alguns casos, você pode encontrar o LCF após algumas tentativas para cada número. Continue neste exemplo até encontrar um mínimo múltiplo comum para 5 e 8. Esse é o seu kgf
5 x 4 = 20
5 x 5 = 25
5 x 6 = 30
5 x 7 = 35
5 x 8 = 40
8 x 4 = 32
8 x 5 = 40
5 x 4 = 20
5 x 5 = 25
5 x 6 = 30
5 x 7 = 35
5 x 8 = 40
8 x 4 = 32
8 x 5 = 40

Método 3 de 4: Use uma tabela de múltiplos comuns

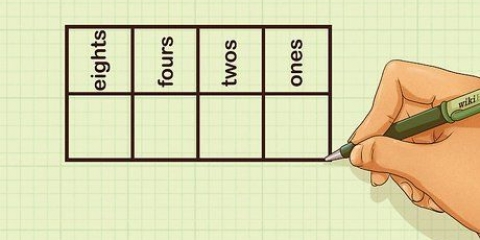
1. Escreva os números no topo de uma tabela de múltiplos comuns. Deixe algum espaço no lado esquerdo dos números e o máximo de espaço possível abaixo dos números. Suponha que temos os números 18, 12 e 30. Escreva cada número em sua própria coluna, no topo da tabela.

2. Escreva o menor fator primo comum dos números no espaço à esquerda. Procure o menor fator primo (como 2, 3 ou 5) que você pode fatorar de todos os números. Eles são todos números pares, então pelo menos 2 é possível.

3. Divida cada um dos números que você está assumindo pelo fator primo comum. Escreva o quociente sob cada número. Isto é o que vai parecer:

4. Repita o processo de fatoração e divisão pelo menor fator primo até que não haja mais fatores. Repita para os números 9, 6 e 15.




5. Se dois dos números ainda compartilham um fator primo comum, continue este procedimento até que nenhum dos números de baixo tenha um fator comum. Quanto a este exemplo, agora você terminou.

6. Multiplique todos os números da primeira coluna pelos fatores primos comuns, com os números na parte inferior de todas as outras colunas. Este é o KGV. Neste exemplo, o produto da coluna de fatores comuns é igual a 6 (2 x 3). Multiplique 6 pelos números na parte inferior das outras colunas: 6 x 3 x 2 x 5 = 180.

Método 4 de 4: algoritmo de Euclides
1. Use o algoritmo de Euclides para encontrar o máximo divisor comum (GGD) de dois números. Suponha que os dois números em um exemplo210 e 45 são. Aqui está um exemplo de como usar o algoritmo de Euclides para encontrar o GGD de ambos os números:
- Divida o primeiro número pelo segundo: 210/45 = 4 (resíduo 30). Isso significa que 210 = 4 x 45 + 30.





2. Multiplique os dois números originais. 210 x 45 = 9.450

3. Divida o resultado pelo GGD de ambos os números. 9.450/15 = 630. 630 é o LCF de 210 e 45.

4. Use o algoritmo de Euclides para encontrar o LCF de três números. Para fazer isso, basta procurar o GCD de dois números e depois usar esse GGD para encontrar o VCF desses dois números e do terceiro número.
Pontas
- Se você quiser saber se o VCF é menor ou maior que o produto, use este método: se o GGD for 1, então o VCF é o produto. Se o GGD for maior que 1, o VCGV será menor que o produto.
- O KGV tem muitas aplicações. O mais comum é que, ao somar ou subtrair frações, elas devem ter o mesmo denominador; se este não for o caso, você terá que torná-los homônimos, para que eles tenham o mesmo denominador. A melhor maneira de fazer isso é procurar o mínimo denominador comum - que é simplesmente o mesmo que o LCF dos denominadores. Por exemplo, para calcular 1/6 + 3/8, vamos encontrar o LCF de 6 e 8, que é 24, e então converter cada fração para que ambos os denominadores sejam iguais a 24, deixando a soma assim: 4/24 + 24/09. Agora podemos simplesmente calcular isso, somando o numerador, com a resposta: 13/24.
- Se você precisar encontrar o LCF de mais de 2 números, seu método acima terá que mudar um pouco, pois só funciona para 2 números ao mesmo tempo. Por exemplo, para encontrar o LCF de 16, 20 e 32, começamos encontrando o LCF de 16 e 20 (que é igual a 80) e depois o LCF de 80 e 32, que dá 160.
- Por exemplo, para encontrar o CHF de 16 e 20, pegamos o GGD de 16 e 20, que dá 4. 16 × 20 = 320 e 320 ÷ 4 = 80, então 80 é o KGV.
- Se você quiser fazer uma fração do mesmo nome, precisará saber quantas vezes cada denominador vai no LCF. Usando este método, você pode encontrar o fator de conversão multiplicando todos os números na parte inferior de todas as outras colunas (exceto a primeira onde todos os fatores primos estão listados). Então, para converter 18 em 180, multiplique por 2 e 5. Para converter 12 em 180, multiplique por 3 e 5.Para converter 30 em 180, multiplique por 3 e 2.
Necessidades
- Lápis.
- Apagador.
- Calculadora (opcional).
Artigos sobre o tópico "Encontre o mínimo múltiplo comum de dois números"
Оцените, пожалуйста статью
Popular