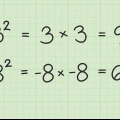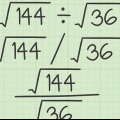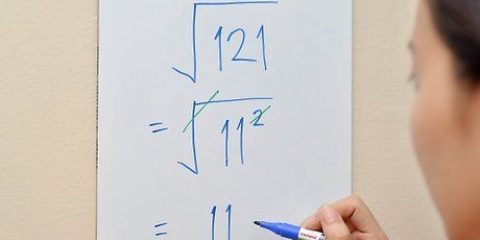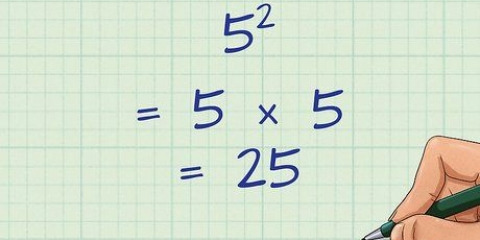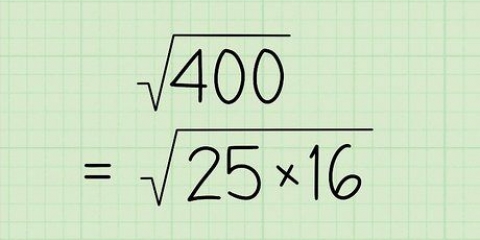Simplificando Raízes Quadradas

Contente

Degraus
Pontas
Avisos

Simplificar uma raiz quadrada não é tão difícil quanto parece. Para simplificar uma raiz quadrada você só precisa fatorar o número da raiz quadrada e tentar tirar a raiz quadrada de um ou ambos os fatores. Uma vez que você conhece alguns números quadrados comuns e sabe como dividir um número em fatores, você está no caminho certo para simplificar uma raiz quadrada. Veja como você pode aprender isso rapidamente.

Degraus

Método 1 de 4: Simplificando a raiz quadrada de um número

Imagem intitulada Simplifique uma Raiz Quadrada Passo 1

1. Aprenda alguns números quadrados e suas raízes. Elevar ao quadrado, multiplicar um número por ele mesmo, faz um número ao quadrado (quadrado perfeito). Por exemplo: 25 é um número ao quadrado porque 5 x 5, ou 5, é igual a 25. Conhecer pelo menos os primeiros 10 números de dez quadrados pode ajudar a reconhecer e simplificar as raízes quadradas. Aqui estão os primeiros dez números ao quadrado:

1 = 1
2 = 4
3 = 9
4 = 16
5 = 25
6 = 36
7 = 49
8 = 64
9 = 81
10 = 100

2. Encontrar a raiz quadrada de um número quadrado. Se você vir um número quadrado sob um radical, basta remover o radical (√ ) e escrever a raiz quadrada do número quadrado. Se você já tinha aprendido isso de cor, então está feito. Se o número for muito grande e você não tiver certeza se é um número quadrado, tente encontrar a raiz quadrada com sua calculadora para verificar se produz um bom número redondo. Por exemplo: em √25 você sabe que a resposta é igual a 5 porque 25 é um número ao quadrado.

Método 2 de 4: Simplificando uma raiz quadrada por fatoração

Imagem intitulada Simplifique uma Raiz Quadrada Passo 4

1. Se o número for par, divida por 2. Encontrar os fatores de um número envolve encontrar todos os números que multiplicados juntos produzem esse número, tornando mais fácil determinar sua raiz quadrada. Se for um número par, a primeira coisa que você pode fazer é dividir o número por 2. Neste exemplo você pode dividir √98 em √(2x49), porque 98 : 2 =49. Se o número não for divisível por 2, tente 3, 4, 5 e assim por diante, até encontrar a combinação certa.

Imagem intitulada Simplifique uma Raiz Quadrada Passo 5

2. Divida esses fatores de volta em fatores para encontrar mais números quadrados. Veja se você pode continuar dividindo o número em fatores. 2 é primo e tem apenas ele mesmo e 1 como divisor. Mas 49, o outro fator, ainda pode ser dividido em 7 x 7, porque é um número quadrado. Então você pode reescrever a raiz √(2x49) como √(2x7x7), ou √[2(7)], o que significa que já encontramos o número quadrado que estávamos procurando.

Imagem intitulada Simplifique uma Raiz Quadrada Passo 6

3. Simplifique a raiz quadrada. Como √98= √[2(7)], é possível colocar um 7 fora do radical e simplificar a resposta para 7√2. Então √49 ou também (7 x 7), então se torna 7 assim que você o coloca fora do radical. Se você colocar o 7 de volta, ele se torna um número quadrado novamente e, portanto, 49. Então, √98 = 7√2.

Método 3 de 4: Outros métodos para simplificar uma raiz quadrada

1. Se você não conseguir encontrar imediatamente um número quadrado, divida o número ainda mais. Por exemplo, se o problema for √48, você continua dividindo até não poder ir além de 2x2, de modo que 4 se torne um coeficiente do radical e 3 permaneça dentro do radical. Veja como isso funciona:

√48 = √(2 x 24)
√(2 x 24) = √(2 x 12 x 2)
√(2 x 12 x 2) = √(2 x 6 x 2 x 2)
√(2 x 6 x 2 x 2) = √(2 x 3 x 2 x 2 x 2)
√(2 x 3 x 2 x 2 x 2) = √(2 x 3)
√(2 x 3)= 4√3
√48 = 4√3

2. Lembre-se que você não pode simplificar um número primo. Isso porque os fatores aqui são 1 e o próprio número primo. Por exemplo: √17 não pode ser simplificado porque 17 é primo.

3. Dividindo em fatores de mais de um número ao quadrado. Se os fatores do número contiverem mais de um número quadrado, tire-os todos fora do radical. Se você encontrou vários quadrados ao simplificar, pegue todos fora do radical e multiplique-os. Por exemplo: vamos supor que você queira simplificar o número √32 e depois dividi-lo pelos fatores 4 x 4 x 2, observando que o quadrado do número 4 ocorre duas vezes. Faça este 16√2 que eventualmente renderá 4√2.

4. Não confunda o coeficiente com uma raiz de potência mais alta. 3√125, por exemplo, é igual a 3 x √125, mas √125 é a raiz cúbica de 125. (porque 5 x 5 x 5 = 125, √125 = 5.)

Método 4 de 4: Conhecendo a Terminologia

1. Lembre-se que o radical (√) é o símbolo da raiz quadrada. Por exemplo, no problema √25, "√" o sinal radical.

2. Lembre-se que o radical é o número sob o radical. Encontre a raiz quadrada deste número. Por exemplo: em √25 é "25" o número raiz.

3. Lembre-se que o coeficiente é o número fora do radical. Esse número multiplica a raiz quadrada; Isso pode ser encontrado à esquerda do sinal de radical, o símbolo √. Por exemplo: em 7√2, "7" o coeficiente.

4. Lembre-se que um fator é um número que vai completamente para outro número. Por exemplo: 2 é um fator de 8 porque 8 ÷ 4 = 2, mas 3 não é um fator de 8 porque 8 ÷3 não responde um inteiro. Por exemplo: 5 é um fator de 25 porque 5 x 5 = 25.

5. Entenda o significado de simplificar uma raiz quadrada. Simplificar uma raiz quadrada envolve simplesmente dividir um quadrado de uma raiz quadrada em fatores, depois movê-lo para a esquerda do radical, deixando o outro fator dentro do radical. Se o número for um número quadrado então vocêpoderá remover o sinal de radical assim que tiver escrito sua raiz quadrada. Por exemplo: √98 pode ser simplificado para 7√2.

Pontas

Uma maneira de encontrar quadrados para dividir seus números ao quadrado é procurar quadrados em sua lista começando com o menor número após o número ao quadrado. Por exemplo: se você está procurando o número quadrado de 27, comece em 25 e pare em 9, porque você encontrou o maior divisor que é um número quadrado.

Avisos

Não use calculadoras exceto na etapa em que você está tentando descobrir quantas vezes o quadrado vai para a raiz quadrada.
Simplificar não é o mesmo que colocar valores em uma equação.Em nenhum lugar em todo o processo um número decimal pode aparecer em qualquer lugar!