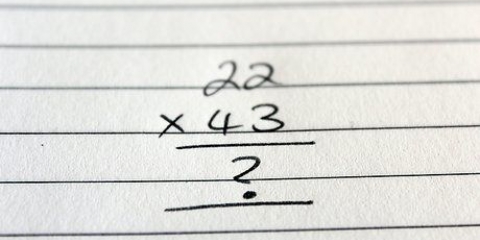Dividindo Números Binários: 13 Passos (com Imagens)

Contente

Degraus
- Método 1 de 2: usando divisão longa
- Método 2 de 2: usando o método do complemento
Pontas

A divisão de números binários pode ser resolvida usando a divisão longa, um método conveniente para aprender o procedimento sozinho ou escrever um programa de computador simples. Alternativamente, o método complemento de subtração repetida oferece uma abordagem com a qual você pode não estar familiarizado, embora não seja muito usado na programação. As linguagens de máquina costumam usar um algoritmo de estimativa para maior eficiência, mas estes não são descritos aqui.

Degraus

Método 1 de 2: usando divisão longa

Imagem intitulada Dividir números binários Passo 1

1. Repasse a divisão longa decimal novamente. Se já faz um tempo desde que você fez uma divisão longa com números decimais regulares (base 10), revise sua base para o problema 172 ÷ 4. Caso contrário, pule isso e vá para a próxima etapa para aprender este procedimento para números binários.

Isto dividendo é dividido pelo divisor, e a resposta é isso quociente.
Compare o divisor com o primeiro dígito do dividendo. Se o divisor for o maior número, continue adicionando dígitos ao dividendo até que o divisor seja o menor número. (Como exemplo, ao calcular 172 ÷ 4, comparamos 4 e 1, descobrimos que 4 > 1, e então compare 4 com 17.)
Escreva o primeiro dígito do quociente acima do último dígito do dividendo usado para comparação. Depois de comparar 4 e 17, notamos que 4 cabe em 17 quatro vezes, então escrevemos 4 como o primeiro dígito do nosso quociente, acima de 7.
Multiplique e subtraia para encontrar o resto. Multiplique o quociente pelo divisor, neste caso 4 x 4 = 16. Escreva o 16 sob o 17, depois faça 17 - 16 para o resto, 1.
Repita. Novamente comparamos o divisor 4 com o próximo dígito, 1, notamos que 4 > 1, e "trazer" movemos o próximo dígito do dividendo para baixo para comparar 4 com 12. 4 vai para 12 três vezes sem resto, então podemos escrever 3 como o próximo dígito do quociente. A resposta é 43.

Imagem intitulada Dividir números binários Passo 2

2. Criar uma configuração de divisão longa binária. Suponha que usemos como exemplo 10101 ÷ 11. Escreva isso como divisão longa, com 10101 como dividendo e 11 como divisor. Deixe um espaço acima dele para escrever o quociente e escreva seus cálculos abaixo dele.

Imagem intitulada Dividir números binários Passo 3

3. Compare o divisor com o primeiro dígito do dividendo. Isso funciona da mesma maneira que a divisão decimal longa, mas na verdade é muito mais fácil na forma binária. Ou você não pode dividir o número pelo divisor (0), ou o divisor cabe uma vez (1):

11 > 1, então 11 "não serve" 1. Escreva um 0 como o primeiro dígito do quociente (acima do primeiro dígito do dividendo).

Imagem intitulada Dividir números binários Passo 4

4. Agora pegue o próximo número e repita até obter 1. Aqui estão os próximos passos do nosso exemplo:

Abaixe o próximo dígito do dividendo. 11 > 10. Escreva um 0 no quociente.

Abaixe o próximo número. 11 < 101. Escreva um 1 no quociente.

Imagem intitulada Divide Binary Numbers Step 5

5. Determinar o resto. como na divisão decimal longa, multiplicamos o dígito que acabamos de encontrar (1) pelo divisor (11) e escrevemos o resultado abaixo do nosso dividendo em uma linha com o dígito que acabamos de calcular. Na forma binária, podemos fazer isso mais rápido, porque 1 x o divisor sempre é igual ao divisor:

Escreva o divisor abaixo do dividendo. Aqui escrevemos isso como 11 sob os três primeiros dígitos (101) do dividendo.

Calcule 101 - 11 para o resto, 10. Revise como subtrair números binários se você não se lembrar.

Imagem intitulada Dividir números binários Passo 6

6. Continue até que o problema seja resolvido. Traga o próximo dígito do revendedor para o resto abaixo para obter 100. Porque 11 < 100 você escreve um 1 como o próximo dígito do quociente. Continue resolvendo o problema como antes:

Escreva 11 sob 100 e subtraia esses números para obter 1.

Abaixe o último dígito do dividendo e você receberá 11 como resposta.

11 = 11, então você escreve 1 como o último dígito do quociente (a resposta).

Não há resto, então a tarefa está concluída. A resposta é 00111, ou mais simples, 111.

Imagem intitulada Dividir números binários Passo 7

7. Adicione um ponto de base, se necessário. Às vezes, o resultado não é um número inteiro. Se você ainda tiver um resto depois de usar o último dígito, adicione um ".0" ao dividendo e um "." ao seu quociente para que você possa diminuir mais um número e seguir em frente. Continue fazendo isso até atingir a precisão desejada e, em seguida, arredonde sua resposta. No papel, você pode arredondar omitindo o 0 ou, se o último dígito for 1, subtrair e adicionar 1 ao último dígito. Ao programar, use um dos algoritmos de arredondamento padrão para evitar erros ao converter entre números binários e decimais.

A divisão de números binários geralmente resulta em números repetidos após o ponto decimal, mais frequentemente do que aqueles que ocorrem com notação decimal.

Isto é referido pelo termo mais geral "ponto de base" que você encontra em qualquer sistema numérico, porque você tem a "ponto decimal" encontrado apenas no sistema decimal.

Método 2 de 2: usando o método do complemento

Imagem intitulada Dividir números binários Passo 8

1. Entenda a ideia básica. Uma maneira de resolver divisões – para qualquer base – é continuar subtraindo o divisor do dividendo, depois o resto, calculando quantas vezes você pode continuar fazendo isso antes de chegar a um número negativo. Aqui está um exemplo para a base 10, o problema 26 ÷ 7:

26 - 7 = 19 (1 vezes subtraído)
19 - 7 = 12 (2 vezes subtraído)
12 - 7 = 5 (3 vezes subtraído)
5 - 7 = -2. Número negativo, então para cima novamente. A resposta é 3 com resto 5. Observe que este método não leva em consideração os dígitos decimais.

Imagem intitulada Dividir Números Binários Passo 9

2. Aprenda a subtrair usando complementos. Embora você possa aplicar facilmente o método acima a números binários, também podemos usar um método mais eficiente, que pode economizar tempo ao programar divisões binárias. Isso é chamado de método do complemento binário. Aqui está o básico, onde calculamos 111 - 011 (certifique-se de que ambos os números tenham o mesmo comprimento):

Encontre o complemento das unidades do segundo termo, subtraindo cada dígito de 1. Você pode fazer isso facilmente com números binários definindo cada 1 para 0 e cada 0 para 1. No nosso exemplo, 011 é igual a 100.

Adicione 1 ao resultado: 100 + 1 = 101. Isso é chamado de complemento de 2. Vamos agora considerar uma soma negativa como uma soma de adição. A essência é que consideramos o problema como se estivéssemos adicionando um número negativo em vez de subtrair um número positivo, após concluir o procedimento.

Adicione o resultado ao primeiro termo. Resolva a soma: 111 + 101 = 1100.

Omitir o primeiro dígito (carregar dígito). Remova o primeiro dígito da sua resposta para obter o resultado final. 1100 → 100.

Imagem intitulada Divide Binary Numbers Step 10

3. Combine os dois conceitos acima. Agora você sabe como funciona o método de subtração para resolver divisões e o método de complemento de 2 para resolver as somas de menos. Você pode combinar os dois em um método para resolver problemas de divisão, usando as etapas abaixo. Se você quiser, pode tentar descobrir por si mesmo antes de continuar.

Imagem intitulada Divide Binary Numbers Step 11

4. Subtraia o divisor do dividendo adicionando o complemento de 2. Vamos resolver o seguinte problema: 100011 ÷ 000101. O primeiro passo é resolver 100011 - 000101, usando o método do complemento de 2, para que se torne uma soma:

complemento de 2 de 000101 = 111010 + 1 = 111011

100011 + 111011 = 1011110

Omitir o primeiro dígito (o carry) → 011110

Imagem intitulada Divide Binary Numbers Step 12

5. Adicione 1 ao quociente. Em um programa de computador, este é o ponto em que você aumenta o quociente em 1. No papel, faça uma anotação em um canto em algum lugar, onde não vai atrapalhar o resto do seu trabalho. Agora fizemos com sucesso um mínimo uma vez, então o quociente até agora é 1.

Imagem intitulada Divide Binary Numbers Step 13

6. Repita subtraindo o divisor do resto. O resultado do nosso último cálculo é o resto deixado após o divisor uma vez "entrou". Continue adicionando o complemento de 2 do divisor e subtraindo o transporte. Adicione 1 ao quociente de cada vez e continue até obter um resto igual ao seu divisor menor:

011110 + 111011 = 1011001 → 011001 (quociente 1+1=10)

011001 + 111011 = 1010100 → 010100 (quociente 10+1=11)

010100 + 111011 = 1001111 → 001111 (11+1=100)

001111 + 111011 = 1001010 → 001010 (100+1=101)

001010 + 111011 = 10000101 → 0000101 (101+1=110)

0000101 + 111011 = 1000000 → 000000 (110+1=111)

0 é menor que 101, então podemos parar agora. O quociente 111 é a resposta para o subproblema. O resto é o resultado final do nosso mínimo, neste caso 0 (sem descanso).

Pontas

As instruções de incremento, decremento ou pilha devem ser consideradas antes de aplicar um cálculo binário a um conjunto de instruções de máquina.
O método de complemento de 2 para subtração não funciona se os números consistem em um número diferente de dígitos. Adicione zeros extras ao número menor para resolver isso.
Ignore o dígito com sinal em números binários com sinal antes de fazer o cálculo, exceto ao tentar descobrir se uma resposta é positiva ou negativa.