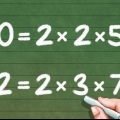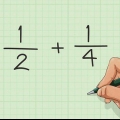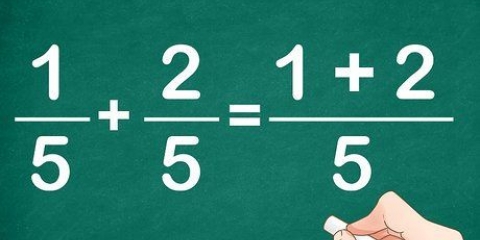Encontre o Mínimo Múltiplo Comum de Dois Denominadores

Contente

Degraus
Necessidades

Para adicionar ou subtrair frações com denominadores diferentes. é necessário primeiro encontrar o mínimo múltiplo comum desses dois números. Este é o menor múltiplo de qualquer denominador em uma equação. Aqui estão alguns métodos diferentes que você pode usar para encontrar o lcm e usá-los para resolver problemas de fração.

Degraus

Método 1 de 4: listar múltiplos

Imagem intitulada Encontre o mínimo denominador comum Passo 1

1. Liste os múltiplos de cada denominador. Cada lista deve consistir no denominador da fração multiplicado por 1, 2, 3, 4 e assim por diante.

Exemplo: 1/2 + 1/3 + 1/5
Múltiplos de 2: 2 *1=2; 2 *2=4; 2 *3=6; 2 *4=8; 2 *5=10; 2 *6=12; 2 *7=14; etc.
Múltiplos de 3: 3 *1=3; 3 *2=6; 3 *3=9; 3 *4=12; 3 *5=15; 3 *6=18; 3 *7=21; etc.
Múltiplos de 5: 5 *1=5; 5 *2=10; 5 *3=15; 5 *4=20; 5 *5=25; 5 *6=30; 5 *7=35; etc.

Imagem intitulada Encontre o Denominador Mínimo Comum Passo 2

2. Encontre o mínimo múltiplo comum. Percorra cada lista e destaque qualquer múltiplo comum de ambos os denominadores. Após determinar os múltiplos comuns, determine qual é o menor.

Observe que, se atualmente não houver múltiplo comum, você deve continuar até encontrar um múltiplo que seja válido para ambos os denominadores.

Exemplo: 2 *15=30; 3 *10=30; 5 *6=30

O kgv=30

Imagem intitulada Encontre o Denominador Mínimo Comum Passo 3

3. Reescreva o problema original. Para escrever cada fração dessa soma de forma que ela tenha o mesmo valor do problema original, é necessário multiplicar o numerador e o denominador da fração pelo valor apropriado, que corresponde ao múltiplo comum encontrado.

Exemplo: 15 *(1/2); 10 *(1/3); 6 *(1/5)

Nova soma: 15/30 + 10/30 + 6/30

Imagem intitulada Encontre o Denominador Mínimo Comum Passo 4

4. Resolver. Depois de encontrar o LCF e as frações terem sido modificadas, você poderá resolver esse problema sem problemas.

Exemplo: 15/30 + 10/30 + 6/30=31/30=1 1/30

Método 2 de 4: Usando o máximo divisor comum

Imagem intitulada Encontre o Denominador Mínimo Comum Passo 5

1. Encontre o máximo divisor comum de cada denominador. Descubra se existe um máximo divisor comum para ambos os denominadores, descobrindo quais números são divisíveis pelos denominadores.

Exemplo: 3/8 + 5/12
Fatores de 8: 1, 2, 4, 8
Fatores de 12: 1, 2, 3, 4, 6, 12

Imagem intitulada Encontre o Denominador Mínimo Comum Passo 6

2. Identifique o máximo divisor comum entre os dois denominadores. Circule todos os GCDs depois de encontrar os fatores de cada denominador. O maior dos GCDs é o maior denominador comum que você pode usar para resolver ainda mais o problema.

Em nosso exemplo, 8 e 12 compartilham o denominador 1, 2 e 4.

O máximo divisor comum é 4.

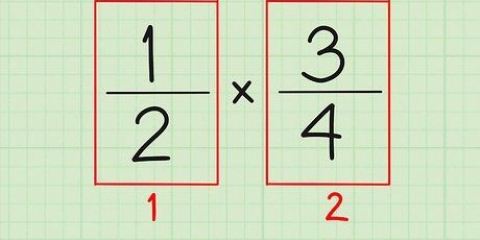
3. Multiplique os denominadores juntos. Vá para o próximo passo multiplicando os dois denominadores juntos.

Exemplo: 8 * 12 = 96

Imagem intitulada Encontre o Denominador Mínimo Comum Passo 7

4. Compartilhe pelo gcd. Depois de encontrar o produto de ambos os denominadores, divida isso pelo mdc encontrado anteriormente. O resultado desta divisão é o seu mínimo múltiplo comum.

Exemplo: 96 / 4=24

Imagem intitulada Encontre o Denominador Mínimo Comum Passo 8

5. Reescreva o problema original. Reescreva os numeradores multiplicando-os pelo mesmo número necessário para tornar os denominadores correspondentes iguais ao lcg. Encontre o fator para cada fração dividindo o lcm pelo denominador original.

Exemplo: 24/8=3; 24/12=2

3 *(3/8)=9/24; 2 *(5/12)=10/24

24/09 + 24/10

Imagem intitulada Encontre o Denominador Mínimo Comum Passo 9

6. Resolva o problema. Com o kgv encontrado agora deve ser possível somar e subtrair sem problemas.

Exemplo: 24/09 + 24/10 = 24/19

Método 3 de 4: Fatorando frações em fatores primos

Imagem intitulada Encontre o Denominador Mínimo Comum Passo 10

1. Divida os denominadores em primos. Divida cada denominador em uma série de números primos. Lembre-se que os primos são aqueles números que não podem ser divididos por nenhum outro número exceto 1 e ele mesmo.

Exemplo: 1/4 + 1/5 + 1/12
Os fatores primos de 4: 2 * 2
Os fatores primos de 5: 5
Os fatores primos de 12: 2 *2 *3

Imagem intitulada Encontre o Denominador Mínimo Comum Passo 11

2. Conte o número de vezes que cada número primo ocorre no conjunto de fatores primos. Turf o número de vezes que cada número primo ocorre nos fatores primos de cada denominador.

Exemplo: Existem dois 2-e em 4; zero 2-e em 5; dois 2-e em 12

Existem zero 3-e em 4 e 5; uma 3 em 12

Existem zero 5-e em 4 e 12; uma 5 em 5

Imagem intitulada Encontre o Denominador Mínimo Comum Passo 12

3. Pegue o maior número para qualquer número primo. Observe quantas vezes você usou cada número primo.

Exemplo: O maior número para 2 é dois; o maior número para 3 é um; o maior número para 5 é um.

Imagem intitulada Encontre o Denominador Mínimo Comum Passo 13

4. Escreva isso como um exemplo abaixo.

Exemplo: 2, 2, 3, 5

Imagem intitulada Encontre o Denominador Mínimo Comum Passo 14

5. Multiplique todos os primos assim. Multiplique os números primos da série anterior. O produto desses números é igual ao lcm do problema original.

Exemplo: 2 *2 *3 *5=60

kgf=60

Imagem intitulada Encontre o Denominador Mínimo Comum Passo 15

6. Reescreva o problema original. Divida o LCF pelo denominador original. Multiplique cada numerador pelo mesmo número necessário para tornar o denominador correspondente o LCF.

Exemplo: 60/4=15; 60/5=12; 60/12=5

15 *(1/4)=15/60; 12 *(1/5)=12/60; 5 *(1/12)=5/60

15/60 + 12/60 + 5/60

Imagem intitulada Encontre o Denominador Mínimo Comum Passo 16

7. Resolver. Com o LCF encontrado e os denominadores semelhantes, tornou-se fácil adicionar e subtrair as frações como de costume.

Exemplo: 15/60 + 12/60 + 5/60=32/60=8/15

Método 4 de 4: Trabalhando com números inteiros e mistos

Imagem intitulada Encontre o Denominador Mínimo Comum Passo 17

1. Converta qualquer número inteiro e misto em uma fração imprópria. Converta números mistos em frações impróprias multiplicando o inteiro antes da fração pelo denominador e adicionando o numerador ao produto. Converta um inteiro em uma fração imprópria colocando-o como numerador em uma fração com o denominador `1`.

Exemplo: 8 + 2 1/4 + 2/3
8=8/1
2 1/4; 2 *4 + 1=8 + 1=9; 04/09
Trabalho reescrito: 8/1 + 9/4 + 2/3

Imagem intitulada Encontre o Denominador Mínimo Comum Passo 18

2. Encontre o mínimo múltiplo comum dos denominadores. Aplique um dos métodos para encontrar o LCF de uma fração comum, conforme descrito acima. Observe que neste exemplo estamos usando o método `Listando múltiplos`, criando uma lista de múltiplos para cada denominador e derivando o lcm deste.

Observe que você não precisa listar múltiplos de 1 porque todo número é um múltiplo de 1.

Exemplo: 4 *1=4; 4 *2=8; 4 *3=12; 4 *4=16; etc.

3 *1=3; 3 *2=6; 3 *3=9; 3 *4=12; etc.

O kgv=12

Imagem intitulada Encontre o Denominador Mínimo Passo 19

3. Reescreva o problema original. Em vez de apenas multiplicar o denominador, é necessário também multiplicar o numerador pelo número necessário para tornar o denominador um lcg.

Exemplo: 12 *(8/1)=96/12; 3 *(9/4)=27/12; 4 *(2/3)=8/12

96/12 + 27/12 + 8/12