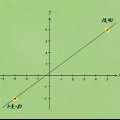
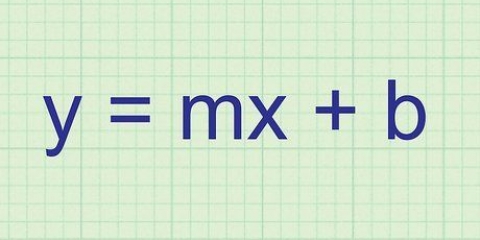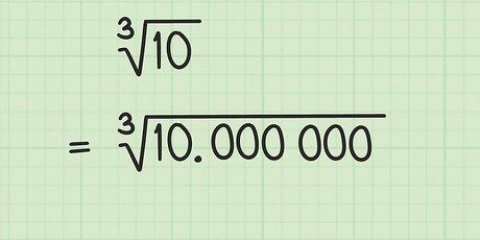O eixo x é o eixo horizontal; o eixo y é o eixo vertical. As coordenadas de um ponto são escritas como  .
. Por exemplo, um segmento de linha pode ter um ponto final em  e outro em
e outro em  .
. 
Por exemplo, com os pontos  e
e  , sua fórmula ficará assim:
, sua fórmula ficará assim: 


Por exemplo:



Por exemplo:



Como você está determinando a raiz quadrada, talvez seja necessário arredondar sua resposta. Como você está trabalhando a partir de um sistema de coordenadas, sua resposta será em geral "unidades" e não em centímetros, metros ou qualquer outra unidade. Por exemplo:

 unidades.
unidades.
Calculando o comprimento de uma linha usando a fórmula da distância
Você pode medir o comprimento de uma linha vertical ou horizontal em um sistema de coordenadas simplesmente adicionando as coordenadas; no entanto, medir o comprimento de uma linha diagonal é um pouco mais complicado. Você pode usar a fórmula de distância para determinar o comprimento de tal linha. Esta fórmula é na verdade o teorema de Pitágoras, que fica claro quando você imagina o segmento de reta como a hipotenusa de um triângulo retângulo. Usando uma fórmula geométrica simples, medir linhas ao longo de várias coordenadas torna-se uma tarefa relativamente simples.
Degraus
Parte 1 de 2: Escrevendo a fórmula

1. Anote a fórmula da distância. A fórmula afirma que  , através do qual
, através do qual  é igual à distância da linha,
é igual à distância da linha,  é igual às coordenadas do primeiro ponto final do segmento de linha, e
é igual às coordenadas do primeiro ponto final do segmento de linha, e  é igual às coordenadas do segundo ponto final do segmento de linha.
é igual às coordenadas do segundo ponto final do segmento de linha.
 , através do qual
, através do qual  é igual à distância da linha,
é igual à distância da linha,  é igual às coordenadas do primeiro ponto final do segmento de linha, e
é igual às coordenadas do primeiro ponto final do segmento de linha, e  é igual às coordenadas do segundo ponto final do segmento de linha.
é igual às coordenadas do segundo ponto final do segmento de linha.
2. Determine as coordenadas dos pontos finais do segmento de linha. Estes podem já ter sido dados. Caso contrário, conte ao longo do eixo x e do eixo y para encontrar as coordenadas.
 .
. e outro em
e outro em  .
.
3. Aplicar as coordenadas à fórmula da distância. Certifique-se de inserir os valores para as variáveis corretas. Os dois  -coordenadas estão dentro dos primeiros parênteses, e os dois
-coordenadas estão dentro dos primeiros parênteses, e os dois  -as coordenadas estão dentro dos próximos dois colchetes.
-as coordenadas estão dentro dos próximos dois colchetes.
 -coordenadas estão dentro dos primeiros parênteses, e os dois
-coordenadas estão dentro dos primeiros parênteses, e os dois  -as coordenadas estão dentro dos próximos dois colchetes.
-as coordenadas estão dentro dos próximos dois colchetes. e
e  , sua fórmula ficará assim:
, sua fórmula ficará assim: 
Parte 2 de 2: Calculando a distância

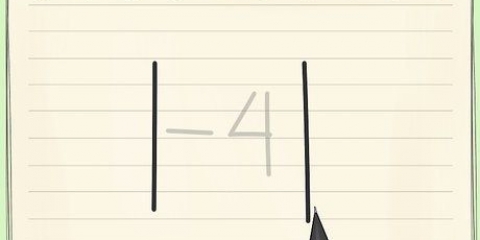
1. Calcule a soma negativa entre parênteses. De acordo com a ordem das operações, cada cálculo entre parênteses deve ser calculado primeiro.
- Por exemplo:

2. Quadrar o valor entre parênteses. A ordem das operações indica que você deve calcular as potências.



3. Adicione os números sob o sinal de radical. Você pode fazer esse cálculo como se estivesse trabalhando com números inteiros.



4. Resolva para d  . Para aproximar a resposta final, encontre a raiz quadrada da soma sob o radical.
. Para aproximar a resposta final, encontre a raiz quadrada da soma sob o radical.
 . Para aproximar a resposta final, encontre a raiz quadrada da soma sob o radical.
. Para aproximar a resposta final, encontre a raiz quadrada da soma sob o radical.
 unidades.
unidades.Pontas
- Não confunda esta fórmula com outras, como a fórmula do ponto médio, a fórmula da inclinação ou a equação de uma linha.
- Tenha em mente a ordem das operações ao calcular a resposta. Primeiro subtraia, depois eleve a diferença ao quadrado, depois some e depois calcule a raiz quadrada.
Artigos sobre o tópico "Calculando o comprimento de uma linha usando a fórmula da distância"
Оцените, пожалуйста статью
Similar
Popular