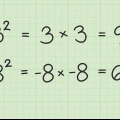Neste exemplo, o primeiro conjunto de três números multiplicados é igual a 10. Determine o maior cubo menor que 10. Isso é 8, e sua raiz cúbica é 2. Escreva o número 2 acima do sinal de radical, acima do número 10. Anote o valor de  , igual a 8, abaixo do número 10; desenhe uma linha e subtraia os números da mesma maneira que na divisão longa. O resultado é 2.
, igual a 8, abaixo do número 10; desenhe uma linha e subtraia os números da mesma maneira que na divisão longa. O resultado é 2. Após esta soma negativa você tem o primeiro dígito da sua resposta. Você terá que verificar se este número é exato o suficiente. Na maioria dos casos não será assim. Você pode verificar isso elevando o número ao cubo e vendo se está próximo o suficiente do resultado desejado. Nesse caso  é igual a 8, e isso não é muito perto de 10, então você tem que seguir em frente.
é igual a 8, e isso não é muito perto de 10, então você tem que seguir em frente. 
À esquerda da linha vertical, escreva a solução do próximo divisor, como a soma de três números separados. Indique os espaços em branco para esses números sublinhando três espaços em branco com sinais de mais abaixo deles. 


Agora calcule 3 vezes 10 vezes cada um dos dois números que existem em sua solução acima do radical. Para este problema simples, isso significa 3*10*2*1, que é igual a 60. Adicione isso aos 1200 que você já tinha e você obtém 1260. Finalmente, adicione o quadrado do último dígito. Neste exemplo, é 1; e 1^2 ainda é 1. Então o divisor total é 1200+60+1, ou 1261. Observe isso à esquerda da linha vertical. 

Você pode verificar a precisão deste resultado usando o cubo: 2,1*2,1*2,1. O resultado é 9.261. Se você acha que o resultado é exato o suficiente, você pode parar. Se você quiser uma resposta mais exata, terá que passar por outra rodada. 
Pegue o próximo grupo de três números para baixo. Neste caso, são três zeros, que vêm após o restante 739 e, portanto, 739.000 formas. Comece o divisor em 300 vezes o quadrado do número atualmente acima do radical. Isto é  , e, portanto, 132.300.
, e, portanto, 132.300. Selecione o próximo dígito da sua solução para que você possa multiplicá-lo por 132.300 e menos do 739.000 do seu restante. Uma boa escolha seria 5, porque 5*132.300=661.500. Escreva o número 5 no próximo espaço acima da linha radical. Encontre 3 vezes o número anterior acima da linha radical, 21, vezes o último dígito que você acabou de escrever, 5, vezes 10. Isto dá  .
. Finalmente, você eleva o último dígito ao quadrado. Isto é 
Some os termos do seu divisor e você terá 132.300+3150+25=135.475. 
Multiplique o divisor pelo último dígito da sua solução. 135.475*5=677.375. subtrair. 739.000-677.375=61.625. Considere se a solução 2.15 é exata o suficiente. Calcule seu cubo e você terá  .
. 


No problema de exemplo, 600 (seu número de destino) fica a meio caminho entre os números limite 512 e 729. Então escolha seu 5 como seu próximo número. 
Neste exemplo, você multiplica 

Por exemplo, neste problema,  maior que o alvo (600). Então você reduz a estimativa para 8,4. Pegue o cubo desse número e compare-o com o seu alvo. você vai ver isso
maior que o alvo (600). Então você reduz a estimativa para 8,4. Pegue o cubo desse número e compare-o com o seu alvo. você vai ver isso  . Isso agora é menor do que seu alvo. Isso informa que a raiz cúbica de 600 deve ser pelo menos 8,4, mas menor que 8,5.
. Isso agora é menor do que seu alvo. Isso informa que a raiz cúbica de 600 deve ser pelo menos 8,4, mas menor que 8,5. 
Neste problema de exemplo, sua última rodada de cálculos mostra que  , enquanto
, enquanto  . O alvo (600) está ligeiramente mais próximo de 592 do que de 614. Então você estima o próximo número um pouco menos da metade entre 0 e 9. Uma boa escolha é 4, que lhe dará uma estimativa da raiz cúbica de 8,44.
. O alvo (600) está ligeiramente mais próximo de 592 do que de 614. Então você estima o próximo número um pouco menos da metade entre 0 e 9. Uma boa escolha é 4, que lhe dará uma estimativa da raiz cúbica de 8,44. 
Para este problema de exemplo, comece observando que  . Isso está logo acima do alvo, então solte alguns e teste 8.43. Isto dá
. Isso está logo acima do alvo, então solte alguns e teste 8.43. Isto dá  como resultado. Então você sabe que a raiz cúbica de 600 é um pouco maior que 8,43 e um pouco menor que 8,44.
como resultado. Então você sabe que a raiz cúbica de 600 é um pouco maior que 8,43 e um pouco menor que 8,44. 
Para o exemplo da raiz cúbica de 600, assumindo dois números decimais, 8,43 está a menos de 1 do número alvo. Se você continuar com três dígitos após o ponto decimal, verá que  se o resultado for 0,1 a menos que a resposta real.
se o resultado for 0,1 a menos que a resposta real. 

Para saber mais sobre o binômio de Newton e obter este resultado, leia mais sobre a multiplicação de binômios no wikiHow. Se você quiser uma versão mais aprofundada e rápida, leia mais sobre o Triângulo de Pascal. 

O primeiro termo contém um plural de 1000. Você primeiro escolhe um número que pode ser elevado ao cubo e ainda permanece dentro do intervalo de divisão longa como o primeiro dígito. Isso produz o termo 1000A^3 no binômio. O segundo termo do binômio de Newton tem um coeficiente de 300. (Isto é de  .) Lembre-se que ao calcular a raiz cúbica, o primeiro dígito de cada etapa foi multiplicado por 0300.
.) Lembre-se que ao calcular a raiz cúbica, o primeiro dígito de cada etapa foi multiplicado por 0300. O segundo dígito em cada etapa do cálculo da raiz cúbica vem do terceiro termo do binômio de Newton. No binômio de Newton você vê o termo 30AB^2. O último dígito de cada etapa é o termo B^3. 
Calculando as raízes cúbicas manualmente
Contente
Usando uma calculadora, calcular a raiz cúbica de qualquer número é apenas pressionar algumas teclas. Mas talvez você não tenha uma calculadora ou queira impressionar seus amigos com sua habilidade de calcular uma raiz cúbica de improviso. Existe um método que parece um pouco difícil à primeira vista, mas funciona muito facilmente com um pouco de prática. É útil ter algum conhecimento pronto no campo de habilidades aritméticas e cálculo de números cúbicos.
Degraus
Parte 1 de 3: Elaborando uma tarefa de amostra

1. Preparar a tarefa. Resolver a raiz cúbica de um número parecerá resolver uma divisão longa, com algumas diferenças aqui e ali. O primeiro passo é anotar o problema corretamente.
- Anote o número que você deseja encontrar a raiz cúbica de. Escreva os números em grupos de três, onde a vírgula é o ponto de partida. Neste exemplo você vai encontrar a raiz cúbica de 10. Escreva isso como 10.000.000. Os zeros são necessários para a precisão da resposta.
- Desenhe um radical do cubo sobre o número. Isso serve ao mesmo propósito que a linha de divisão longa. A única diferença é a forma do símbolo.
- Coloque uma vírgula acima da linha, diretamente acima do ponto decimal no número original.

2. Conheça os cubos das unidades. Você usará isso em seus cálculos. Diz respeito aos seguintes terceiros poderes:











3. Encontre o primeiro dígito da sua resposta. Selecione um número que, para o cubo, dê o maior resultado possível que seja menor que o primeiro conjunto de três números.
 , igual a 8, abaixo do número 10; desenhe uma linha e subtraia os números da mesma maneira que na divisão longa. O resultado é 2.
, igual a 8, abaixo do número 10; desenhe uma linha e subtraia os números da mesma maneira que na divisão longa. O resultado é 2. é igual a 8, e isso não é muito perto de 10, então você tem que seguir em frente.
é igual a 8, e isso não é muito perto de 10, então você tem que seguir em frente.
4. Faça a escalação para o próximo dígito. Escreva o próximo grupo de três números no restante e desenhe uma linha vertical curta à esquerda do número resultante. Este será o número que usaremos para determinar o próximo dígito em sua solução de raiz cúbica. Neste exemplo, será 2000, que é criado a partir do restante 2 da soma negativa anterior, com o grupo de três zeros que você tirou.

5. Encontre o início do próximo divisor. Para a primeira parte do divisor, escreva trezentos vezes o quadrado do que estiver acima do radical. Neste caso, são 2; 2^2 é 4 e 4*300=1200. Então escreva 1200 no primeiro espaço vazio. O divisor para esta etapa da solução será 1200, mais outra coisa que você calculará em um minuto.

6. Encontre o próximo número em sua raiz cúbica. Encontre o próximo dígito da sua solução selecionando o que você pode multiplicar pelo divisor (1200-e-alguma coisa) e, em seguida, subtraia do restante de 2000. Isso só pode ser 1, porque 2 vezes 1200 é igual a 2400, que é maior que 2000. Escreva o número 1 no próximo espaço acima do radical.

7. Encontre o resto do divisor. O divisor nesta etapa da solução consiste em três partes. A primeira parte são os 1200 que você já tem. Agora você precisará adicionar dois termos extras para completar o divisor.

8. Multiplicar e subtrair. Arredonde esta parte da solução multiplicando o último dígito da sua solução - neste caso o número 1 - vezes o divisor que você acabou de calcular (1261). 1*1261 =1261. Escreva isso abaixo de 2000 e subtraia 1261 dele para obter 739.

9. Decida que você deve ir mais longe para obter uma resposta mais precisa. Depois de completar a soma negativa de cada etapa, você deve verificar se sua resposta é exata o suficiente. Para a raiz cúbica de 10: após a primeira soma negativa, a raiz cúbica era apenas 2, e isso não é realmente exato. Agora, após a segunda rodada, a solução é 2,1.

10. Determinar o dealer para a próxima rodada. Neste caso, para mais prática e uma resposta mais precisa, repita os passos para outra rodada, da seguinte forma:
 , e, portanto, 132.300.
, e, portanto, 132.300. .
.

11. Multiplique o divisor pelo resultado. Após calcular o divisor nesta próxima rodada e expandir sua solução em mais um dígito, proceda da seguinte forma:
 .
.
12. Anote sua resposta final. O resultado acima do radical é a raiz cúbica, com uma precisão de três dígitos significativos. Neste exemplo, a raiz cúbica de 10 é igual a 2,15. Verifique isso calculando 2,15^3=9,94, que pode ser arredondado para 10. Se precisar de uma resposta mais precisa, continue até ficar satisfeito.
Parte 2 de 3: Encontrando a raiz cúbica por meio de estimativas repetidas

1. Use números cúbicos para definir os limites superior e inferior. Quando solicitado pela raiz cúbica de um determinado número, comece escolhendo um cubo que esteja o mais próximo possível dele, sem ser maior que o seu número alvo.
- Por exemplo, se você quiser encontrar a raiz cúbica de 600, lembre-se (ou use uma tabela de cubos) que
e
. Portanto, a solução para a raiz cúbica de 600 será algo entre 8 e 9. Use os números 512 e 729 como limites superior e inferior para sua solução.

2. Adivinhe o próximo número. Você conhecia o primeiro dígito por causa do seu conhecimento de certos números cúbicos. Para o próximo dígito, estime um número entre 0 e 9 com base em onde seu número de destino cai entre os dois números de limite.

3. Teste seu palpite determinando seu cubo. Tente multiplicar a estimativa com a qual está trabalhando agora para ver o quão perto você está do número de destino.


4. Ajuste sua estimativa quando necessário. Depois de aumentar para o cubo do seu último palpite, verifique o resultado em relação ao seu número alvo. Se o resultado for maior que a meta, sua estimativa deve ser menor. Se o resultado for menor que o objetivo, você deve ajustá-lo para cima até atingir o objetivo.
 maior que o alvo (600). Então você reduz a estimativa para 8,4. Pegue o cubo desse número e compare-o com o seu alvo. você vai ver isso
maior que o alvo (600). Então você reduz a estimativa para 8,4. Pegue o cubo desse número e compare-o com o seu alvo. você vai ver isso  . Isso agora é menor do que seu alvo. Isso informa que a raiz cúbica de 600 deve ser pelo menos 8,4, mas menor que 8,5.
. Isso agora é menor do que seu alvo. Isso informa que a raiz cúbica de 600 deve ser pelo menos 8,4, mas menor que 8,5.
5. Estime o próximo número para uma resposta mais precisa. Continue este procedimento de estimar números de 0 a 9, até que sua resposta seja tão precisa quanto você deseja. Para cada rodada de estimativa, comece verificando a posição do seu último cálculo entre os números do limite.
 , enquanto
, enquanto  . O alvo (600) está ligeiramente mais próximo de 592 do que de 614. Então você estima o próximo número um pouco menos da metade entre 0 e 9. Uma boa escolha é 4, que lhe dará uma estimativa da raiz cúbica de 8,44.
. O alvo (600) está ligeiramente mais próximo de 592 do que de 614. Então você estima o próximo número um pouco menos da metade entre 0 e 9. Uma boa escolha é 4, que lhe dará uma estimativa da raiz cúbica de 8,44.
6. Continue estimando e ajustando Faça isso quantas vezes forem necessárias, eleve sua estimativa ao cubo e veja como ela se compara ao número alvo. Procure por números que estão logo abaixo ou logo acima do número alvo.
 . Isso está logo acima do alvo, então solte alguns e teste 8.43. Isto dá
. Isso está logo acima do alvo, então solte alguns e teste 8.43. Isto dá  como resultado. Então você sabe que a raiz cúbica de 600 é um pouco maior que 8,43 e um pouco menor que 8,44.
como resultado. Então você sabe que a raiz cúbica de 600 é um pouco maior que 8,43 e um pouco menor que 8,44.
7. Continue até atingir a precisão desejada. Continue estimando, comparando e reestimando, pelo tempo que for necessário, até que sua solução seja tão precisa quanto você deseja. Observe que, a cada decimal, seus números de destino se aproximam cada vez mais do número real.
 se o resultado for 0,1 a menos que a resposta real.
se o resultado for 0,1 a menos que a resposta real.Parte 3 de 3: Entenda como esse cálculo funciona

1. Revise o binômio de Newton novamente. Para entender por que esse algoritmo funciona para determinar as raízes cúbicas, você deve primeiro pensar em como o cubo se parece como binomial. Você provavelmente aprendeu isso na matemática do ensino médio (e como a maioria das pessoas, você provavelmente esqueceu muito rapidamente). Selecione duas variáveis  e
e  para representar unidades. Então você calcula o binômio de
para representar unidades. Então você calcula o binômio de  para as dezenas.
para as dezenas.
 e
e  para representar unidades. Então você calcula o binômio de
para representar unidades. Então você calcula o binômio de  para as dezenas.
para as dezenas. - Use o termo
para criar uma dúzia. Qualquer que seja o grau que você selecionar
,
vai formar uma dúzia. Por exemplo, se
é 2 e
é 6, então . se torna
igual a 26.

2. Escreva o binômio em um cubo. Agora trabalhamos de trás para frente, primeiro determinando o cubo e depois vendo por que a solução de raízes cúbicas funciona. Precisamos dos valores de  achar. Você faz isso trabalhando
achar. Você faz isso trabalhando  . Este é um cálculo muito longo para mostrar aqui, mas o resultado final é
. Este é um cálculo muito longo para mostrar aqui, mas o resultado final é  .
.
 achar. Você faz isso trabalhando
achar. Você faz isso trabalhando  . Este é um cálculo muito longo para mostrar aqui, mas o resultado final é
. Este é um cálculo muito longo para mostrar aqui, mas o resultado final é  .
.
3. Conheça o significado de divisão longa. Observe que o método para calcular a raiz cúbica funciona como a divisão longa. Na divisão longa você vê que dois fatores multiplicados juntos, dê o número com o qual você começou. Neste cálculo, o número que você está procurando (o número que termina acima do radical) é a raiz cúbica. Isso significa que é igual ao termo (10A+B). Os reais A e B são irrelevantes agora, desde que você entenda a relação com a resposta.

4. Veja a versão estendida. Quando você olha para o binômio de Newton, você vê porque o algoritmo da raiz cúbica está correto. Veja como o divisor em cada etapa do algoritmo é igual à soma dos quatro termos que você precisa calcular e somar. Esses termos surgem da seguinte forma:
 .) Lembre-se que ao calcular a raiz cúbica, o primeiro dígito de cada etapa foi multiplicado por 0300.
.) Lembre-se que ao calcular a raiz cúbica, o primeiro dígito de cada etapa foi multiplicado por 0300.
5. Assista a Precisão Crescer. Trabalhando a divisão longa, cada passo que você completa dá grande precisão à sua resposta. Por exemplo, o problema de exemplo elaborado neste artigo é para determinar a raiz cúbica de 10. No primeiro passo, a solução é 2, porque  chega perto, mas é inferior a 10. Na verdade,
chega perto, mas é inferior a 10. Na verdade,  . Após a segunda rodada, sua solução é 2,1. Depois de resolver isso, você terá
. Após a segunda rodada, sua solução é 2,1. Depois de resolver isso, você terá , e isso está muito mais próximo do resultado desejado (10). Após a terceira rodada você tem 2,15, e isso lhe dá
, e isso está muito mais próximo do resultado desejado (10). Após a terceira rodada você tem 2,15, e isso lhe dá  . Continue trabalhando em grupos de três números e você obterá uma resposta tão precisa quanto desejar.
. Continue trabalhando em grupos de três números e você obterá uma resposta tão precisa quanto desejar.
 chega perto, mas é inferior a 10. Na verdade,
chega perto, mas é inferior a 10. Na verdade,  . Após a segunda rodada, sua solução é 2,1. Depois de resolver isso, você terá
. Após a segunda rodada, sua solução é 2,1. Depois de resolver isso, você terá , e isso está muito mais próximo do resultado desejado (10). Após a terceira rodada você tem 2,15, e isso lhe dá
, e isso está muito mais próximo do resultado desejado (10). Após a terceira rodada você tem 2,15, e isso lhe dá  . Continue trabalhando em grupos de três números e você obterá uma resposta tão precisa quanto desejar.
. Continue trabalhando em grupos de três números e você obterá uma resposta tão precisa quanto desejar.Pontas
- Como qualquer coisa, suas habilidades matemáticas melhorarão com a prática. Quanto mais você praticar, melhor será capaz de fazer esses tipos de cálculos.
Avisos
- É fácil cometer um erro aqui. Verifique seu trabalho com cuidado e refaça a elaboração.
Necessidades
- Caneta ou lápis
- Papel
- Governante
- Apagador
Artigos sobre o tópico "Calculando as raízes cúbicas manualmente"
Оцените, пожалуйста статью
Similar
Popular