Para encontrar s³, multiplique s três vezes por ele mesmo: s³ = s x s x s 
Se você não tem 100% de certeza se sua forma é um cubo, meça todos os lados para ver se eles são iguais. Se não forem, você terá que usar o método abaixo para calcular o volume de uma viga. Nota: Nas fotos de amostra as medidas são dadas em polegadas (pol), porém usamos centímetros (cm). 




Exemplo: O comprimento desta viga é 4 cm, então l = 4 cm. Não se preocupe muito com qual lado é o comprimento, etc. Contanto que você meça apenas três lados diferentes, o resultado será o mesmo. 
Exemplo: A largura desta viga é de 3 cm, então b = 3 cm. Se você medir a viga com uma régua ou fita métrica, não se esqueça de anotar tudo na mesma unidade de medida. 
Exemplo: A altura desta barra é 6 cm, então h = 6 cm. 
Neste exemplo, l = 4, b = 3 e h = 6. Portanto, o resultado é V = 4 x 3 x 6 = 72. 
Por exemplo, se as dimensões da viga fossem em metros, você obteria l = 2 m, w = 4 m e h = 8 m. O volume seria então 2 m x 4 m x 8 m = 64 m³. 

Na maioria dos casos é suficiente arredondar pi para 3,14. Pergunte ao seu professor o que ele quer. A fórmula para encontrar o volume de um cilindro é na verdade muito parecida com a do volume de uma viga: você multiplica a altura da forma pela área da base. Para uma viga, a área da base é l x b, para um cilindro é π x r², a área de um círculo com raio r. 

Outra opção é medir a circunferência do círculo (a distância ao redor dele) com um pedaço de barbante ou uma fita métrica. Então coloque o resultado nesta fórmula: C (circunferência) é 2 x π x r. Divida a circunferência por 2 x π (6,28) e você terá o raio. Por exemplo, se a circunferência que você mediu é de 8 cm, então o raio é de 1,27 cm. Se você realmente precisa de uma medida exata, pode usar qualquer um dos métodos para ver se os resultados são os mesmos. Se não, verifique novamente. O método da circunferência geralmente dá um resultado mais preciso. 
Se o raio é 4 cm, então a área do círculo é A = π x 4². 4² = 4 x 4, ou 16. 16 xπ = 16 x 3,14 = 50,24 cm². Se o diâmetro da base for conhecido, em vez do raio, lembre-se de que d = 2 x r. Então você tem que dividir o diâmetro por dois para encontrar o raio. 

V = π x 4² x 10 π x 4²= 50,24 50,24 x 10 = 502,4 V = 502,4 


A fórmula para pirâmides retas, onde o vértice está diretamente acima do centro da base, é a mesma das pirâmides inclinadas, onde o vértice não está no centro. 
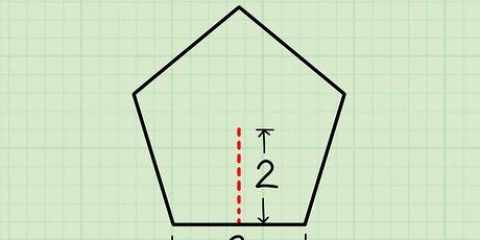
A fórmula para a área de um triângulo é A = 1/2 x b x h, onde b é a base e h é a altura. É possível calcular a área de qualquer polígono regular com a fórmula A = 1/2 xpxa, onde A é a área, p é o perímetro e a é o apótema, que é a distância do centro da forma até o centro de um dos lados. Você também pode facilitar a si mesmo e usar uma calculadora de polígono regular on-line. 

Se tivéssemos outra pirâmide com base com área de 26 e altura de 8, o resultado teria sido: 1/3 x 26 x 8 = 69,33. 


A parte π x r² refere-se à área do círculo que forma a base do cone. Então a fórmula para o volume do cone é 1/3 x w x h, assim como a fórmula para a pirâmide no método acima! 
Neste exemplo o raio é 3 cm. Se colocarmos isso na fórmula, obtemos: A = π x 3². 3² = 3 x 3, ou 9, então A = π x 9. A = 28,27 cm². 


No nosso exemplo que é 141,35 x 1/3 = 47,12, o volume do cone. Novamente: 1/3 x π x 3² x 5 = 47,12. 




Por exemplo, se você mede a bola e vê que a circunferência é 18 cm, divida isso por 6,28, você sabe que o raio é 2,87 cm. Pode ser complicado medir uma esfera, por isso é melhor medi-la três vezes e fazer a média (somar as três medidas e dividir por três) para obter a medida o mais precisa possível. Por exemplo, se você mediu três vezes e os resultados foram 18 cm, 17,75 cm e 18,2 cm, some esses valores (18 + 17,5 + 18,2 = 53,95) e divida por 3 (53,95/3 = 17,98). Você usa essa média ao calcular o volume. 


Então, em nosso exemplo, torna-se 36 x 3,14 = 113,09. 
Calcular volume
Contente
O volume de uma figura é o espaço tridimensional que a figura ocupa. Você pode representar o volume como a quantidade de água (ou ar, areia, etc.).) que caberia no molde se estivesse completamente cheio. As unidades de medida de volume comumente usadas são centímetros cúbicos e metros cúbicos.Este artigo irá ensiná-lo a calcular o volume de seis formas tridimensionais diferentes comumente encontradas em testes de matemática, incluindo o cubo, a esfera e o cone. Você verá que existem muitas semelhanças que tornarão mais fácil para você lembrar. Veja se você pode encontrar essas correspondências!
Degraus
Método 1 de 6: Calculando o volume de um cubo

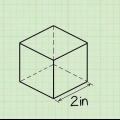
1. Reconhecer um cubo. Um cubo é uma forma tridimensional com seis faces quadradas idênticas.Em outras palavras, é uma caixa com lados iguais em todos os lugares.
- Um dado é um bom exemplo de cubo que você pode ter em casa. Cubos de açúcar ou blocos infantis também costumam ser cubos.

2. Aprenda a fórmula para calcular o volume do cubo. Como todos os comprimentos dos lados do cubo têm o mesmo comprimento, a fórmula para calcular o volume do cubo é muito fácil. O lugar onde dois lados se encontram é chamado de costela. Abreviamos o volume para "V". As costelas, ou o comprimento do lado, chamamos aqui "s". A fórmula então se torna V = s³

3. Encontre o comprimento de um lado do cubo. Dependendo da tarefa, essa informação pode já estar lá, mas você também pode ter que medi-la com uma régua. Lembre-se, como é um cubo, todos os comprimentos dos lados devem ser iguais, então não importa qual você mede.

4. Coloque o comprimento do lado na fórmula V = s³ e calcule. Por exemplo, se você mediu que o comprimento do lado do seu cubo é 5 cm, você escreveria a fórmula da seguinte forma: V = (5)³. 5 x 5 x 5 = 125 cm³, então esse é o volume do seu cubo!

5. Certifique-se de escrever sua resposta em centímetros cúbicos. No exemplo acima, o cubo foi medido em centímetros, então a resposta deve ser dada em centímetros cúbicos. Se o comprimento do lado do cubo fosse 3 metros, então o volume teria sido V = (3 m)³ = 27 m³.
Método 2 de 6: Calculando o volume de um feixe.

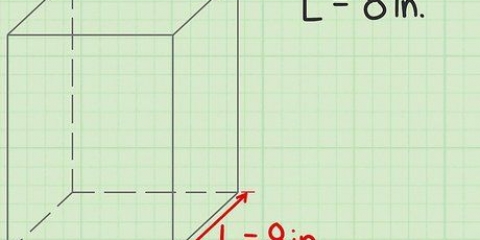
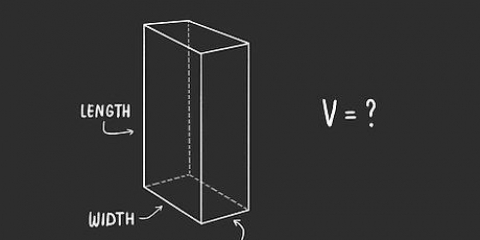
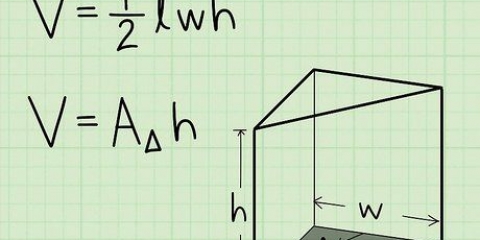
1. Reconhecer um feixe. Uma viga é uma figura que consiste em seis superfícies retangulares. Na verdade, é um retângulo tridimensional, uma espécie de caixa.
- Na verdade, um cubo é apenas uma viga especial, onde todos os lados são iguais.

2. Aprenda a fórmula para calcular o volume de uma viga. A fórmula para o volume de uma viga é V = comprimento (l) x largura (w) x altura (h), ou V = l x w x h. Nota: As imagens que acompanham estes exemplos mostram "C" para largura.

3. Encontre o comprimento da viga. O comprimento é o lado mais longo da viga que é paralelo ao solo ou superfície sobre a qual repousa. O comprimento pode já estar indicado na imagem, ou pode ser necessário medi-lo com uma régua.

4. Encontre a largura da viga. A largura da viga pode ser encontrada medindo o lado curto que é paralelo ao solo ou superfície sobre a qual ela repousa. Novamente, verifique primeiro se já está indicado na imagem e meça de outra forma com sua régua.

5. Encontre a altura da viga. Altura é a distância do solo ou superfície em que a viga repousa até o topo da viga. Veja se já está indicado na imagem e meça diferente com sua régua ou fita métrica.

6. Insira as dimensões na fórmula e calcule-a. Lembre-se que V = l x w x h.

7. Certifique-se de escrever sua resposta em centímetros cúbicos. O resultado é, portanto, 72 centímetros cúbicos, ou 72 cm³.
Método 3 de 6: Calculando o Volume de um Cilindro

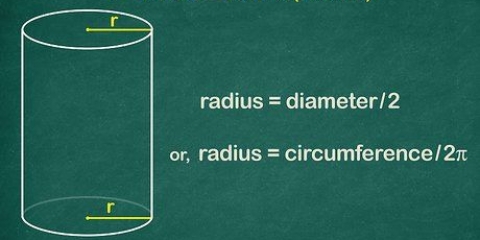
1. Aprenda a identificar um cilindro. Um cilindro é uma forma tridimensional com duas extremidades redondas idênticas conectadas por um único lado curvo. Na verdade, é uma haste reta e redonda.
- Uma lata é um bom exemplo de cilindro ou bateria AA.

2. Memorize a fórmula do volume de um cilindro. Para calcular o volume de um cilindro, você precisa saber sua altura e o raio de sua base circular.O raio é a distância do centro do círculo até a borda. A fórmula é V = π x r² x h, onde V é o volume, r é o raio, h é a altura e π é a constante pi.

3. Encontre o raio da base. Se já estiver indicado na imagem, basta preenchê-lo. Se você obteve o diâmetro em vez do raio, basta dividir por 2 para encontrar o raio (d = 2 x r).

4. Meça a forma se o raio não for fornecido. Observe que pode ser difícil medir o raio exato de um círculo. Uma opção é medir o círculo em seu ponto mais largo com a régua de cima para baixo, dividindo-o por dois.

5. Calcule a área do círculo na base. Coloque o raio na fórmula π x r². Multiplique o raio por ele mesmo e multiplique esse resultado por π. Por exemplo:

6. Encontre a altura do cilindro. Esta é simplesmente a distância entre as duas bases circulares, ou a distância da superfície sobre a qual o cilindro repousa até o topo do cilindro. Veja se o comprimento já está indicado na imagem, ou meça de forma diferente com sua régua ou fita métrica.

7. Multiplique a área da base pela altura do cilindro para encontrar o volume. Coloque os valores na fórmula V =π x r² x h. No nosso exemplo com um raio de 4 cm e uma altura de 10 cm:

8. Lembre-se de escrever sua resposta em centímetros cúbicos. Neste exemplo, o cilindro foi medido em centímetros, então a resposta deve ser escrita em centímetros cúbicos: V = 502,4cm³. Se o cilindro fosse medido em metros, o volume teria que ser escrito em metros quadrados (m³).
Método 4 de 6: Calculando o Volume de uma Pirâmide Regular

1. Saiba o que é uma pirâmide regular. Uma pirâmide é uma forma tridimensional com um polígono na base e lados que se afunilam para o topo (a ponta da pirâmide).Uma pirâmide regular é uma pirâmide cuja base é um polígono regular, o que significa que todos os lados e ângulos desse polígono são iguais.
- Normalmente, uma pirâmide é representada com uma base quadrada e lados que se afunilam em um ponto, mas a base de uma pirâmide pode ter 5, 6 ou 100 lados!
- Uma pirâmide com um círculo como base é chamada de cone, que discutiremos no próximo método.

2. Aprenda a fórmula para calcular o volume da pirâmide regular. A fórmula para o volume de uma pirâmide regular é V = 1/3 x b x h, onde b é a área da base e h é a altura da pirâmide, ou a distância vertical da base ao topo.

3. Calcule a área da base. A fórmula para isso depende do número de lados da base. No nosso exemplo, a base é um quadrado com lados de 6 cm. Lembre-se que a fórmula para calcular a área de um quadrado é A = s². Então com nossa pirâmide que é 6 x 6 = 36 cm².

4. Encontre a altura da pirâmide. Na maioria dos casos, será indicado na imagem. No nosso exemplo, a altura da pirâmide é 10 cm.

5. Multiplique a área da base da pirâmide pela altura e divida por 3 para encontrar o volume. Lembre-se que a fórmula é V = 1/3 x b x h. No nosso exemplo, a pirâmide tem uma base com área de 36 e altura de 10, então o volume é 36 x 10 x 1/3 = 120.

6. Lembre-se de escrever o resultado em unidades cúbicas. As medidas da pirâmide no exemplo foram dadas em centímetros, então o resultado deve ser escrito em centímetros cúbicos, 120 cm³. Se as medidas foram dadas em metros, escreva a resposta em metros cúbicos (m³).
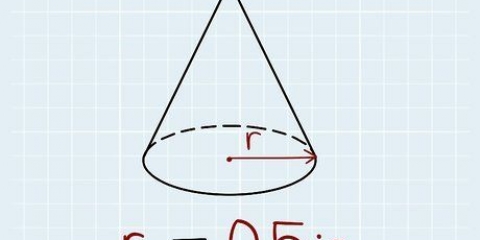
Método 5 de 6: Calculando o Volume de um Cone

1. Aprenda quais são as propriedades de um cone. Um cone é uma forma tridimensional com uma base circular e um único ponto na face oposta. Outra maneira de ver um cone é que é um tipo especial de pirâmide com uma base circular.
- Se a ponta do cone estiver diretamente acima do centro da base, ele é chamado de cone reto. Se não estiver diretamente acima do centro, é chamado de cone oblíquo. Felizmente, a fórmula para calcular o volume é a mesma para os dois tipos de cones.

2. Conheça a fórmula para calcular o volume do cone. Esta fórmula é V = 1/3 x π x r² x h, onde r é o raio do círculo na base, h é a altura do cone e π é a constante pi, que pode ser arredondada para 3,14.

3. Calcule a área da base circular do cone. Para fazer isso, você precisa saber o raio da base, que deve ser indicado na sua foto. Se você obteve o diâmetro em vez do raio, basta dividir esse número por 2, porque o diâmetro é 2 vezes o raio (d = 2 x r). Em seguida, coloque o raio na fórmula A = π x r² para calcular a área.

4. Encontre a altura do cone. Esta é a distância vertical da base do cone até o topo. No nosso exemplo, a altura do cone é de 5 cm.

5. Multiplique a altura do cone pela área da base. No nosso exemplo, a área da base é 28,27cm² e a altura é 5cm, então w x h = 28,27 x 5 = 141,35.

6. Agora multiplique este resultado por 1/3 (ou divida por 3) para obter o volume do cone. Na etapa acima, calculamos o volume de um cilindro, que é um cone onde as paredes ficariam na vertical e terminariam em outro círculo. Dividindo por 3 dá o volume do cone.

7. Lembre-se de escrever o resultado em unidades cúbicas. Nosso cone foi medido em centímetros, então o volume deve ser expresso em centímetros cúbicos: 47,12 cm³.
Método 6 de 6: Calculando o Volume de uma Esfera

1. Reconhecer uma esfera. Uma esfera é uma forma tridimensional perfeitamente redonda, na qual todos os pontos de sua superfície são equidistantes do centro. Em outras palavras, é uma bola.

2. Aprenda a fórmula para calcular o volume de uma esfera. A fórmula é V = 4/3 x π x r³ (ou seja: "quatro terços pi vezes cúbico r"), onde r é o raio da esfera e π é a constante pi (3.14).

3. Encontre o raio da esfera. Se o raio já está dado na imagem, é fácil. Dado o diâmetro, divida este número por 2 para obter o raio. O raio da esfera neste exemplo é de 3 centímetros.

4. Meça a esfera se o raio não for dado. Se você precisar medir uma esfera (como uma bola de tênis) para encontrar o raio, encontre uma corda longa o suficiente para enrolá-la completamente. Em seguida, enrole-o ao redor do objeto no ponto mais largo e marque o ponto onde a corda se junta. Depois meça essa parte do barbante com uma régua para saber a circunferência da esfera. Divida isso por 2 x π, ou 6,28, então você sabe o raio.

5. Eleve o raio à terceira potência para encontrar r³. Elevar à terceira potência significa simplesmente multiplicar o número três vezes por ele mesmo, então r³ = r x r x r. Em nosso exemplo r=3 que se torna 3 x 3 x 3 = 27.

6. Multiplique sua resposta por 4/3. Você pode fazer isso com uma calculadora, ou apenas faça você mesmo e simplifique a fração. No nosso exemplo é 27 x 4/3 = 180/3, ou 36.

7. Multiplique o resultado por π para encontrar o volume da esfera. O último passo no cálculo do volume é multiplicar o resultado até agora por π. Arredonde π para duas casas decimais, isso é suficiente para a maioria dos problemas de matemática (a menos que seu professor diga o contrário), então multiplique por 3,14 e você terá sua resposta.

8. Escreva sua resposta em unidades cúbicas. Em nosso exemplo, medimos em centímetros, então a resposta é V = 113,09 cm³.
Artigos sobre o tópico "Calcular volume"
Оцените, пожалуйста статью
Popular