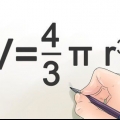Calculando o Volume de um Cone: 5 Passos (com Imagens)

Contente

Degraus
- Método 1 de 1: Calculando o volume de um cone
Pontas
Avisos

Você pode calcular facilmente o volume de um cone se souber sua altura e raio. A fórmula para calcular o volume é então a seguinte: v = hπr/3. Abaixo, explicamos em etapas fáceis.

Degraus

Método 1 de 1: Calculando o volume de um cone

Imagem intitulada Calcular o Volume de um Cone Passo 1

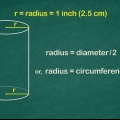
1. Calcule o raio. Se você já conhece o raio, pode pular este passo e ir direto para o passo 2. Se você sabe o diâmetro do círculo, tudo que você precisa fazer é dividi-lo por dois para calcular o raio. Se você conhece a circunferência, calcula o raio dividindo a circunferência por 2π. E se você também não sabe a circunferência, basta pegar uma régua e medir o diâmetro. Em seguida, divida o valor medido por dois e você terá o raio. Suponha que o raio da base desse cone seja 0,5 cm.

Imagem intitulada Calcular o Volume de um Cone Passo 2

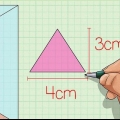
2. Use o raio para calcular a área da base do cone. Para fazer isso, basta usar a fórmula para calcular a área de um círculo: A = r. No lugar de "r" preenchemos 5: A = π(0,5), ou pi vezes 0,5 ao quadrado A = π(0,5) = 0,79 cm .

Imagem intitulada Calcule o volume de um cone Passo 3

3. Meça a altura do cone. Se você já sabe a altura, tudo o que você precisa fazer é anotá-la. Use uma régua se você ainda não souber a altura. Suponha que a altura do nosso cone seja 1,5 cm. Nota: você deve sempre certificar-se de que a altura é indicada na mesma unidade do raio; neste caso centímetros.

Imagem intitulada Calcular o Volume de um Cone Passo 4

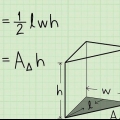
4. Multiplique a área da base pela altura do cone. Multiplique 0,79 cm por 1,5 cm. 0,79 cm x 1,5 cm = 1,19 cm.

Imagem intitulada Calcular o Volume de um Cone Passo 5

5. Divida o resultado por três. Divida 1,19 cm por 3 para calcular o volume do cone. 1,19 cm/3 = 0,40 cm.

Pontas

Certifique-se de que suas medidas são exatas.
É assim que funciona:

Você realmente calcula o volume de um cone primeiro fingindo que está lidando com um cilindro. Nesse caso, você pega a área da base e multiplica pela altura do cilindro. E um cilindro sempre cabe exatamente 3 cones de mesma altura e com a mesma superfície de base. então se você dividir o volume de um cilindro por três você obtém o volume de três cones que cabem no cilindro.

O raio, a altura e o apótema (do vértice do cone até um ponto da circunferência) formam um triângulo retângulo. Assim, podemos aplicar o teorema de Pitágoras a este.

Use sempre a mesma unidade para as diferentes medidas.