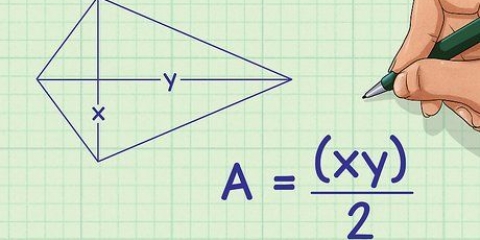Registre esta medida como uma. Exemplo: a = 2cm 
Observe que esta etapa calcula a área de uma face do cubo. Exemplo: a = 2cm a = 2 x 2 = 4 cm 
Esta etapa completa o cálculo da área do cubo. Exemplo: a = 4cm Área = 6 x a = 6 x 4 = 24 cm 

Meça o comprimento da base para determinar o comprimento do prisma e atribua-o a c. Exemplo: c = 5cm Meça a largura da base para determinar a largura do prisma e chame-o de uma. Exemplo: a = 2cm Meça a altura do lado para determinar a altura do prisma e chame-o de b. Exemplo: b = 3 cm 
Exemplo: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 cm 
Exemplo: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 cm 
Exemplo: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 cm 
Exemplo: Área = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 cm. 

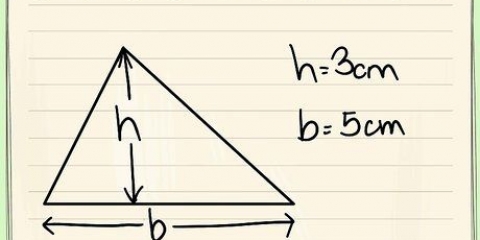
A base b, é igual ao comprimento da base do triângulo. Exemplo: b = 4 cm A altura h da base triangular é igual à distância entre a borda inferior e a ponta. Exemplo: h = 3 cm A área de um triângulo multiplicado por 2 = 2(1/2)b*h = b*h = 4*3 =12 cm 
Exemplo: H = 5 cm Os três lados referem-se aos três lados da base triangular. Exemplo: S1 = 2 cm, S2 = 4 cm, S3 = 6 cm 
Exemplo: P = S1 + S2 + S3 = 2 + 4 + 6 = 12 cm 
Exemplo: P x A = 12 x 5 = 60 cm 
Exemplo: 2A + PH = 12 + 60 = 72 cm. 

Exemplo: r = 3 cm 
Exemplo: r = r x r = 3 x 3 = 9 cm 
Exemplo: π*r = 3,14 x 9 = 28,26 cm 
Exemplo: 4π*r = 4 x 28,26 = 113,04 cm 

Exemplo: r = 3 cm Exemplo: h = 5 cm 
Exemplo: Área da base = π*r = 3,14 x 3 x 3 = 28,26 cm Exemplo: 2π*r = 2 x 28,26 = 56,52 cm 
Exemplo: 2π*rh = 2 x 3,14 x 3 x 5 = 94,2 cm 
Exemplo: 2π*r + 2π*rh = 56,52 + 94,2 = 150,72 cm 

Exemplo: l = 3 cm Exemplo: s = 1 cm 
Exemplo: s = s x s = 1 x 1 = 1 cm 
Exemplo: 2 x s x l = 2 x 1 x 3 = 6 cm 
Exemplo: s + 2 canais = 1 + 6 = 7 cm 

Exemplo: r = 2 cm Exemplo: h = 4 cm 
Exemplo: l = √ (r + h) = √ (2 x 2 + 4 x 4) = √ (4 + 16) = √ (20) = 4,47 cm 
Exemplo: π*r = 3,14 x 2 x 2 = 12,56 cm 
Exemplo: π*rl = 3,14 x 2 x 4,47 = 28,07 cm 
Exemplo: π*r + π*rl = 12,56 + 28,07 = 40,63 cm
Calcular área
Contente
Área é o espaço total ocupado por todas as áreas de um objeto. É a soma de todas as áreas desse objeto. Determinar a área de uma forma tridimensional é bastante fácil, desde que você use a fórmula certa. Cada forma tem sua própria fórmula separada, então você primeiro terá que verificar qual forma é. Calcular a fórmula de área para vários objetos pode facilitar os cálculos no futuro. Aqui discutimos algumas das formas mais comuns que você pode encontrar.
Degraus
Método 1 de 7: Cubo

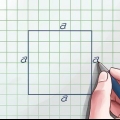
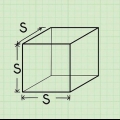
1. Defina a fórmula para a área de um cubo. Um cubo tem seis faces idênticas. Como o comprimento e a largura de um quadrado são iguais, a área de um quadrado é uma, através do qual uma o comprimento é um lado. Como um cubo tem seis faces iguais, você pode calcular sua área multiplicando a área de uma de suas faces por seis. A fórmula da área do cubo O é O = 6a, através do qual uma o comprimento é um lado.
- As unidades de área são um certo comprimento ao quadrado: cm, dm, m, etc.

2. Meça o comprimento de um lado. Por definição, cada lado ou aresta (aresta) de um cubo deve ser igual ao outro, então você só precisa medir um lado. Meça o comprimento do lado com uma régua. Preste atenção às unidades que você usa.

3. Esquadre sua medida para uma. Esquadre a medida para calcular o comprimento da costela. Elevar um valor ao quadrado significa multiplicá-lo por ele mesmo. Se você está aprendendo isso pela primeira vez, pode ser útil lembrar disso como NT= 6*a*a.

4. Multiplique este produto por seis. Lembre-se que um cubo tem seis faces idênticas. Agora que você conhece a área de uma das faces, multiplique por seis (por causa das seis faces).
Método 2 de 7: Prisma retangular

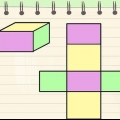
1. Defina a fórmula para a área de um prisma retangular. Como um cubo, um prisma retangular tem seis faces, mas ao contrário de um cubo, essas faces não são iguais. Em um prisma retangular, apenas as faces opostas são iguais entre si. Portanto, ao calcular a área de um prisma retangular, os vários comprimentos das nervuras devem ser levados em consideração, como na fórmula SA = 2ab + 2bc + 2ac.
- Para esta fórmula, uma igual à largura do prisma, b igual à altura e c igual ao comprimento.
- Se olharmos mais de perto a fórmula, você verá que simplesmente somamos todas as áreas de cada face do objeto.
- A unidade de área será um certo comprimento ao quadrado: cm, dm, m, etc.

2. Meça o comprimento, a altura e a largura de cada lado. Todas as três leituras podem ser diferentes, então cada uma deve ser medida separadamente. Meça cada lado com uma régua e registre o valor. Use as mesmas unidades para cada medida.

3. Calcule a área de uma das faces do prisma e multiplique por dois. Lembre-se que existem seis faces em um prisma retangular, e as faces opostas são iguais entre si. Multiplique o comprimento e a altura, ou c e uma, para encontrar a área de um plano. Pegue esta medida e multiplique-a por dois para contabilizar o plano oposto idêntico.

4. Encontre a área da outra face do prisma e multiplique por dois. Assim como no primeiro conjunto de faces, multiplique a largura e a altura, ou uma e b para determinar a área de outra face do prisma. Multiplique esta medida por dois para contabilizar os lados opostos idênticos.

5. Calcule a área das extremidades do prisma e multiplique por dois. As outras duas faces do prisma são as extremidades. Multiplique o comprimento e a largura (c e b) para encontrar sua superfície. Multiplique esta área por dois para contabilizar ambos os lados.

6. Adicione as três áreas separadas juntas. Como a área do prisma é a área total de todas as faces de um objeto, o último passo é somar todas as áreas calculadas individualmente. Some as áreas de todos os lados para obter a área total.
Método 3 de 7: Prisma triangular

1. Defina a fórmula da área para um prisma triangular. Um prisma triangular tem duas faces triangulares idênticas e três faces retangulares. Para encontrar a área, você deve calcular a área de todas as faces e somá-las. A área de um prisma triangular é SA = 2A + PH, onde A é a área da base triangular, P é o perímetro da base triangular e h é a altura do prisma.
- Pois esta fórmula sustenta que uma a área de um triângulo e assim A = 1/2 bh, através do qual b é a base do triângulo e h a altura.
- p é o perímetro do triângulo calculado pela soma das três arestas do triângulo.
- As unidades de área é uma unidade de comprimento ao quadrado: cm, dm, m, etc.

2. Calcule a área do plano triangular e multiplique por dois. A área de um triângulo é /2b*h onde b é a base do triângulo e h é a altura. Então, como existem dois triângulos idênticos como faces, multiplicamos a fórmula por dois. Isso facilita o cálculo para ambos os planos (b*h).

3. Meça cada lado do triângulo e a altura do prisma. Para completar o cálculo da área, você precisa saber o comprimento de cada lado do triângulo e a altura do prisma. A altura é a distância entre as duas faces triangulares.

4. Encontre o perímetro do triângulo. O perímetro do triângulo pode ser calculado somando todos os lados medidos: S1 + S2 + S3.

5. Multiplique a circunferência da base pela altura do prisma. Lembre-se que a altura do prisma é a distância entre as duas faces triangulares. Em outras palavras, multiplique p de Hã.

6. Adicione as duas leituras separadas. Você precisa adicionar as duas medidas das duas etapas anteriores para obter a área do prisma triangular.
Método 4 de 7: Bol

1. Definir a fórmula da área para uma esfera. Uma esfera tem uma superfície curva, então a área da superfície é um valor multiplicado pela constante, pi. A área de uma esfera é calculada usando a equação NT = 4π*r.
- Para esta fórmula, r igual ao raio da esfera. Pi (ou π) pode ser arredondado para 3,14.
- As unidades da área serão uma unidade de comprimento, ao quadrado: cm, dm, m, etc.

2.Meça o raio da lâmpada. O raio da esfera é metade do diâmetro, ou a distância do centro da esfera até a borda.

3. Quadrado do raio. Para elevar ao quadrado um número, multiplique-o por ele mesmo. Multiplique a medida para r com ele mesmo. Lembre-se que esta fórmula pode ser reescrita como SA = 4π*r*r.

4. Multiplique o raio quadrado por um arredondamento de pi. Pi é uma constante que representa a razão entre a circunferência de um círculo e seu diâmetro. É um número irracional com muitos dígitos após o ponto decimal. Geralmente é arredondado para 3,14. Multiplique o raio quadrado por π, ou 3,14, para a área de uma seção transversal circular da esfera.

5. Multiplique este produto por quatro. Para completar o cálculo, multiplique-o por quatro. Encontre a área da esfera multiplicando a área circular plana por quatro.
Método 5 de 7: Cilindro

1. Definir a fórmula da área de um cilindro. Um cilindro tem duas extremidades circulares fechando uma superfície tubular. A fórmula da área de um cilindro é NT = 2π*r + 2π*rh, através do qual r é igual ao raio da base circular e h igual a altura do cilindro. arredondar pi (ou π) diminui para 3,14.
- A fórmula 2π*r calcula a área das duas extremidades circulares, enquanto 2πrh é a área da coluna entre as duas extremidades.
- As unidades de área são uma unidade de comprimento ao quadrado: cm, dm, m, etc.

2. Meça o raio e a altura do cilindro. O raio de um círculo é metade do seu diâmetro, ou a distância do centro do círculo até a borda. A altura é a distância total do cilindro de uma extremidade à outra. Desenhe essas medidas com uma régua e anote-as.

3. Encontre a área da base e multiplique por dois. Para encontrar a área da base, use a fórmula da área ou um círculo (π*r). Para completar o cálculo, eleve o raio ao quadrado e multiplique-o por pi. Em seguida, multiplique por dois por causa do segundo círculo idêntico na outra extremidade do cilindro.

4. Calcule a superfície do próprio cilindro com 2π*rh. Esta é a fórmula para calcular a área de um tubo. O tubo é o espaço entre as duas extremidades circulares do cilindro. Multiplique o raio por dois, pi e a altura.

5. Adicione as duas leituras separadas. Adicione a área dos dois círculos à área do espaço entre os dois círculos para calcular a área total do cilindro. Nota: Ao adicionar essas duas peças, você reconhece a fórmula original: NT =2π*r + 2π*rh.
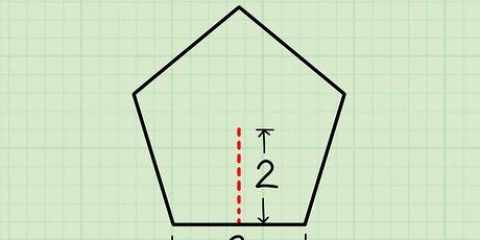
Método 6 de 7: Pirâmide Quadrada

1. Definir a fórmula da área para uma pirâmide quadrada. Uma pirâmide quadrada tem uma base quadrada e quatro lados triangulares. Como mencionado, a área de um quadrado é o comprimento de um lado ao quadrado. A área de um triângulo é 1/2sl (o lado do triângulo vezes o comprimento ou altura do triângulo). Como existem quatro triângulos, você calcula a área total multiplicando-a por quatro. A soma de todas essas faces dá a equação da área de uma pirâmide quadrada: NT = s + 2 canais.
- Nesta equação, s o comprimento de cada lado da base quadrada e eu a altura inclinada de cada lado triangular.
- A unidade de área é uma certa unidade de comprimento ao quadrado: cm, dm, m, etc.

2. Meça a altura inclinada e o lado da base. A altura oblíqua eu, é a altura de um dos lados triangulares. É a distância da base à ponta da pirâmide, medida ao longo de um lado plano. O lado básico s, é o comprimento de um lado da base quadrada. Como a base é quadrada, esta medida é a mesma para todos os lados. Use uma régua para cada medida.

3. Encontre a área da base quadrada. A área de uma base quadrada pode ser calculada ao quadrado do comprimento de um lado (s multiplicar por si mesmo).

4. Calcule a área total das quatro faces triangulares. A segunda parte da equação é a área das quatro faces triangulares restantes. Usando a fórmula 2ls, multiplicamos s de eu e dois. Encontre a área de cada rosto.

5. Adicione as duas áreas separadas juntas. Adicione a área total das faces à área da base para calcular a área total.
Método 7 de 7: Cone

1. Definir a fórmula da área de um cone. Um cone tem uma base circular e uma superfície redonda que afunila em um ponto. Para encontrar a área, pegue a área da base circular e a área do cone, e some os dois. A fórmula da área de um cone é: SA = π*r + π*rl, através do qual r o raio é da base circular, eu a altura oblíqua do cone, e π é a constante pi (3.14).
- A unidade de área é uma certa unidade de comprimento ao quadrado: cm, dm, m, etc.

2. Meça o raio e a altura do cone. O raio é a distância do centro da base circular até a borda da base. Altura é a distância do centro da base até a ponta do cone, medida através do centro do cone.

3. Calcule a altura da inclinação (eu) do cone. Como a altura oblíqua é a hipotenusa real de um triângulo, você precisa encontrar a usando o teorema de Pitágoras por calculá-lo. Use a forma reorganizada, l = √ (r + h), através do qual r o raio é e h a altura do cone.

4. Encontre a área da base circular. A área da base é calculada com a fórmula π*r. Depois de medir o raio, você o eleva ao quadrado (assim você multiplica por ele mesmo) e então você multiplica esse produto por pi.

5. Calcule a área do topo do cone. Use a fórmula π*rl, onde r o raio é do círculo e eu a inclinação conforme calculado acima, para determinar a área do topo do cone.

6. Some as duas áreas para obter a área total do cone. Calcule a área final do cone adicionando a área da base circular ao calcular a etapa anterior.
Necessidades
- Governante
- Caneta ou lápis
- Papel
Artigos sobre o tópico "Calcular área"
Оцените, пожалуйста статью
Popular