Como Calcular o Volume de um Prisma

Contente

Degraus
Pontas

Um prisma é uma figura geométrica com duas extremidades idênticas e lados planos. O prisma é nomeado após a forma de sua base, então um prisma com uma base triangular é chamado de "Prisma triangular." Para calcular o volume de um prisma, basta calcular a área da base e multiplicá-la pela altura – calcular a área da base pode ser a parte complicada. Veja como calcular o volume de vários prismas.

Degraus

Método 1 de 5: Calculando o volume de um prisma triangular

Imagem intitulada Calcular o Volume de um Prisma Passo 1

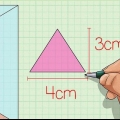
1. Escreva a fórmula para encontrar o volume de um prisma triangular. A fórmula é V = 1/2 x comprimento x largura x altura. Mas, vamos quebrar essa fórmula ainda mais, para obter a fórmula V = área ou base x altura usar. Você pode calcular a área da base, usando a fórmula para encontrar a área de um triângulo -- multiplique 1/2 pelo comprimento e largura da base.

Imagem intitulada Calcular o volume de um prisma Passo 2

2. Determine a área do plano base. Para encontrar o volume de um prisma triangular, você deve primeiro determinar a área da base triangular. Encontre a área da base do prisma multiplicando 1/2 vezes a base do triângulo pela altura.

Ex: se a altura da base triangular é 5 cm e a base do prisma triangular é 4 cm, então a área da base é 1/2 x 5 cm x 4 cm, igual a 10 cm.

Imagem intitulada Calcular o Volume de um Prisma Passo 3

3. Determinar a altura. Suponha que a altura desse prisma triangular seja 7 cm.

Imagem intitulada Calcular o Volume de um Prisma Passo 4

4. Multiplique a área da base triangular pela altura. Multiplique a área da base pela altura. Multiplique a base pela altura e você terá o volume do prisma triangular.

Exemplo: 10 cm x 7 cm = 70 cm

Imagem intitulada Calcular o Volume de um Prisma Passo 5

5. Dê sua resposta em unidades cúbicas. Você deve sempre usar unidades cúbicas ao calcular um volume porque está trabalhando com objetos tridimensionais. A resposta final é 70 cm.

Método 2 de 5: Calculando o volume de um cubo

Imagem intitulada Calcular o Volume de um Prisma Passo 6

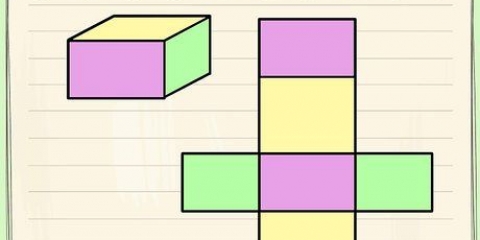
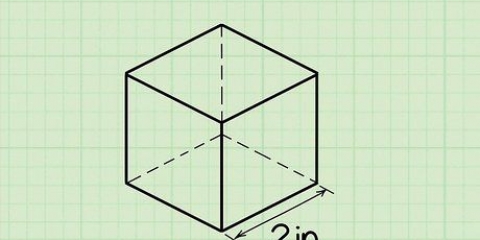
1. Escreva a fórmula para encontrar o volume de um cubo. A fórmula é V = lado. Um cubo é um prisma com 3 lados iguais.

Imagem intitulada Calcular o Volume de um Prisma Passo 7

2. Determine o comprimento de 1 lado do cubo. Todos os lados são iguais, então não importa qual você escolha.

Ex: Comprimento = 3 cm.

Imagem intitulada Calcular o Volume de um Prisma Passo 8

3. O poder de três. Multiplique o número por ele mesmo duas vezes para obter o número cúbico. Um exemplo é "a x a x a". Como todos os comprimentos dos lados são iguais, multiplique dois lados pela área da base e um terceiro lado pela altura. Você pode pensar nisso como uma multiplicação do comprimento, largura e altura, que são todos iguais.

Exemplo: 3 cm = 3 cm. * 3cm. * 3cm. = 27 centímetros.

Imagem intitulada Calcular o Volume de um Prisma Passo 9

4. Dê sua resposta em unidades cúbicas.. A resposta final é 27 cm.

Método 3 de 5: Calculando o volume de um prisma retangular

Imagem intitulada Calcular o Volume de um Prisma Passo 10

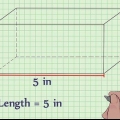
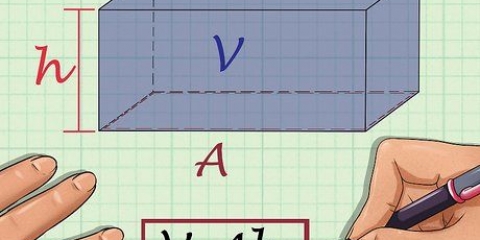
1. Escreva a fórmula para encontrar o volume de um prisma retangular. A fórmula é V = comprimento * largura * altura. Um prisma retangular é um prisma com uma base retangular.

Imagem intitulada Calcular o Volume de um Prisma Passo 11

2. Determine o comprimento. O comprimento é o lado mais longo da superfície plana do retângulo, acima ou abaixo do prisma retangular.

Ex: Comprimento = 10 cm.

Imagem intitulada Calcular o Volume de um Prisma Passo 12

3. Determine a largura. A largura do prisma retangular é o lado mais curto da superfície plana de um retângulo, na parte superior ou inferior da forma.

Ex: Largura = 8 cm.

Imagem intitulada Calcular o Volume de um Prisma Passo 13

4. Determinar a altura. A altura é a parte do prisma retangular que está na vertical. Você pode imaginar a altura do prisma retangular como aquela parte que se estende de um retângulo e faz dele uma figura tridimensional.

Ex: Altura = 5 cm.

Imagem intitulada Calcular o Volume de um Prisma Passo 14

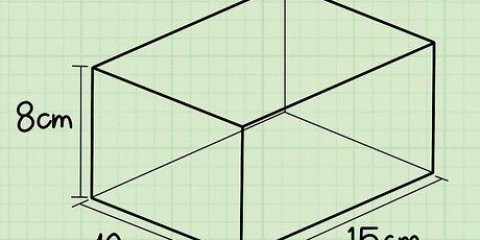
5. Multiplique o comprimento, largura e altura. Multiplique-os em qualquer ordem para o produto. Use este método para encontrar a área da base retangular (10 x 8) e depois o volume multiplicando-o pela altura, 5. No entanto, para encontrar o volume desse prisma, você pode multiplicar os comprimentos do are em qualquer ordem.

Exemplo: 10 cm. * 8cm. * 5cm = 400cm.

Imagem intitulada Calcular o Volume de um Prisma Passo 15

6. Dê sua resposta em unidades cúbicas. A resposta final é 400 cm.

Método 4 de 5: Calculando o volume de um prisma trapezoidal

Imagem intitulada Calcular o Volume de um Prisma Passo 16

1. Escreva a fórmula para calcular o volume de um trapézio. A fórmula é: V = [1/2 x (base₁ + base₂) x altura] x altura do prisma. Use a primeira parte para a área da base do prisma antes de continuar.

Imagem intitulada Calcular o Volume de um Prisma Passo 17

2. Encontre a área da base. Para fazer isso, insira a área da parte superior e inferior na fórmula, juntamente com a altura.

Suponha que a base 1 = 8 cm, a base 2 = 6 cm e a altura = 10 cm.

Ex: 1/2 x (6 + 8) x 10 = 1/2 x 14 cm x 10 cm = 80 cm.

Imagem intitulada Calcular o Volume de um Prisma Passo 18

3. Determine a altura do prisma. Suponha que a altura do prisma seja 12 cm.

Imagem intitulada Calcular o Volume de um Prisma Passo 19

4. Multiplique a área da base pela altura. Para calcular o volume do trapézio, multiplique a área da base pela altura.

80cm x 12cm = 960cm.

Imagem intitulada Calcular o Volume de um Prisma Passo 20

5. Dê sua resposta em unidades cúbicas. A resposta final é 960 cm

Método 5 de 5: Calcular o volume de um prisma pentagonal regular

Imagem intitulada Calcular o Volume de um Prisma Passo 21

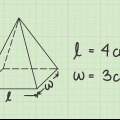
1. Escreva a fórmula para encontrar o volume de um prisma pentagonal regular. A fórmula é V = [1/2 x 5 x lado x apótema] x altura do prisma. Você pode usar a primeira parte da fórmula para encontrar a área da base pentagonal. Pense nisso como determinar a área dos 5 triângulos que juntos formam um polígono regular. O lado é a largura de 1 triângulo e o apótema é a altura de um dos triângulos.Agora você multiplica por 1/2 porque isso faz parte de encontrar a área de um triângulo e depois multiplica isso por 5 porque há 5 triângulos em um pentágono.

Para mais informações sobre como determinar o apótema, veja aqui.

Imagem intitulada Calcular o Volume de um Prisma Passo 22

2. Encontre a área da base pentagonal. Suponha que o comprimento de um lado seja 6 cm e o comprimento do apótema seja 7 cm. Digite os números na fórmula:

A = 1/2 x 5 x lado x apótema

A = 1/2 x 5 x 6 cm x 7 cm = 105 cm

Imagem intitulada Calcular o Volume de um Prisma Passo 23

3. Determinar a altura. Defina a altura do molde é 10 cm.

Imagem intitulada Calcular o Volume de um Prisma Passo 24

4. Multiplique a área da base pentagonal pela altura. Multiplique a área da base pentagonal, 105 cm, vezes a altura, 10 cm, para encontrar o volume do prisma pentagonal comum.

105 cm x 10 cm = 1050 cm

Imagem intitulada Calcular o Volume de um Prisma Passo 25

5. Dê sua resposta em unidades cúbicas. A resposta final é 1050 cm.

Pontas

Experimentar "base" não confundir com "plano básico".Um plano de base refere-se à forma bidimensional que é a base do prisma (geralmente a parte superior e inferior).Mas esse plano de base pode ter sua própria base --- um dos lados da forma do plano, usado para encontrar a área dessa forma.