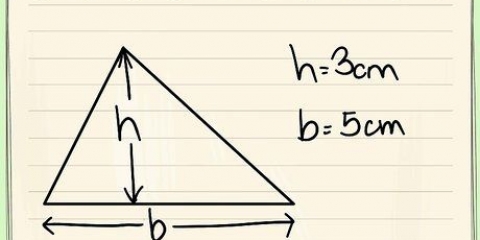
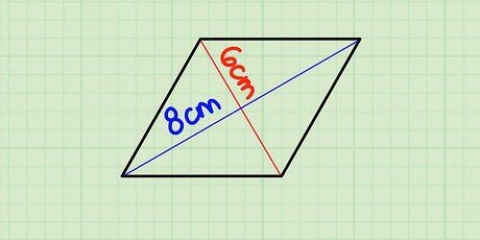
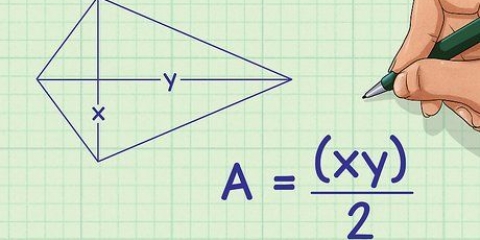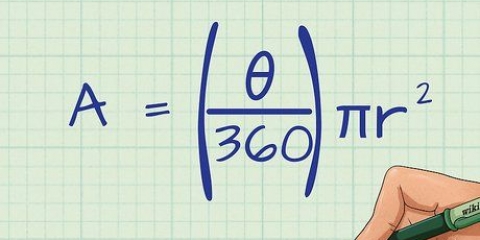No nosso exemplo, a área do triângulo=½ x 3 x 2=3. 
Em nosso exemplo, A(total do pentágono)=5 x A(triângulo)=5 x 3=15. 



O base do triângulo é ½ vezes o lado do pentágono. No nosso exemplo, isso é ½ x 7 = 3,5 unidades. O canto no meio do pentágono é sempre 36º. (Assumindo 360º para um círculo completo, você pode dividir isso em 10 triângulos menores. 360 ÷ 10=36, então o ângulo de tal triângulo é 36º). 
Em um triângulo retângulo, é tangente de um ângulo igual ao comprimento do lado oposto, dividido pelo comprimento do lado adjacente. O lado oposto ao ângulo de 36º é a base do triângulo (metade do lado do pentágono). O lado adjacente do ângulo de 36º é a altura do triângulo. tan(36º)=oposto / adjacente No nosso exemplo, tan(36º)=3,5 / altura altura x bronzeado(36º)=3,5 altura=3,5 / bronzeado(36º) altura=(aprox) 4,8. 
No nosso exemplo, a área de um dos pequenos triângulos é=½bh=½(3,5)(4,8)=8,4. 
No nosso exemplo, a área de todo o pentágono=8,4 x 10=84. 

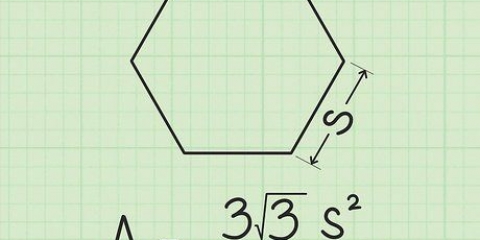
Área de um pentágono regular=(5s ) / (4tan(36º)), onde s= comprimento de um lado. bronzeado(36º)=√(5-2√5). Se a sua calculadora não tiver uma função `tan`, use a fórmula para a área: Area=(5s) / (4√(5-2√5)). 
A área de um pentágono regular=(5/2)rsin(72º), onde r o raio é.
Calcular a área de um pentágono
Contente
Um pentágono é um polígono com cinco lados retos. Quase todos os problemas que você encontrará na aula de matemática envolverão pentágonos regulares, com cinco lados iguais. Existem duas maneiras comuns de calcular a área, dependendo de quanta informação você tem.
Degraus
Método 1 de 3: Determinando a área usando os lados e o apótema

1. Comece com o comprimento do lado e apótema. Este método funciona para pentágonos regulares, com cinco lados iguais. Além do comprimento do lado, você precisa do `apothema` do pentágono. O apótema é a linha do centro do pentágono a um lado, que intercepta o lado perpendicularmente (ou seja, em um ângulo de 90º).
- Não confunda o apótema com o raio de um polígono, pois ele intercepta um ângulo (vértice) em vez de um ponto no meio do lado. Se você conhece apenas o comprimento de um lado e o raio, continue para o próximo método.
- Como exemplo, usamos um pentágono com lado 3 e apótema 2.

2. Divida o pentágono em cinco triângulos. Desenhe cinco linhas do centro do pentágono, cada uma levando a um vértice (canto). Agora você tem cinco triângulos.

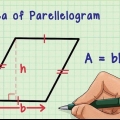
3. Calcular a área de um triângulo. Todo triângulo tem um base igual ao lado do pentágono. Também possui um altura que é igual ao apótema. (Lembre-se, a altura de um triângulo é o comprimento do lado que é perpendicular à sua base e se estende até um vértice). Para calcular a área de um triângulo você usa ½ x base x altura.

4. Multiplique por cinco para a área total do pentágono. Dividimos o pentágono em cinco triângulos iguais. Para calcular a área total, multiplique a área de um triângulo por cinco.
Método 2 de 3: Determinando a área usando o comprimento de um lado

1. Comece com o comprimento de um lado. Este método só funciona para pentágonos regulares, que têm cinco lados de igual comprimento.
- Neste exemplo usamos um pentágono com comprimento 7 para cada lado.

2. Divida o pentágono em cinco triângulos. Desenhe uma linha do centro do pentágono até um vértice. Repita para cada vértice. Agora você tem cinco triângulos, cada um do mesmo tamanho.

3. Divida um triângulo ao meio. Desenhe uma linha do centro do pentágono até a base de um triângulo. Esta linha deve cruzar a base em um ângulo reto (90º), que divide o triângulo em dois triângulos iguais e menores.

4. Rotule um dos triângulos menores. Já podemos rotular um lado e um ângulo do triângulo menor:

5. Calcule a altura do triângulo. O altura deste triângulo é o lado perpendicular ao lado do pentágono que leva ao centro. Usamos trigonometria simples para determinar o comprimento deste lado:

6.Calcule a área do triângulo. A área de um triângulo é igual a ½ base x altura. (A = ½ bh.) Agora que você sabe a altura, insira esses valores para determinar a altura do seu pequeno triângulo.

7. Multiplique para encontrar a área do pentágono. Um desses triângulos menores cobre 1/10 da área do pentágono. Para a área total, multiplique a área do triângulo menor por 10.
Método 3 de 3: usando uma fórmula

1. Use o esboço e apótema. O apótema é uma linha do centro de um pentágono que intercepta um lado em ângulo reto. Se o comprimento for fornecido, você poderá usar esta fórmula simples.
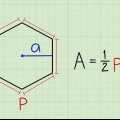
- Área de um pentágono regular =Papai / 2, onde p= a circunferência e uma= o apótema.
- Se você não conhece a circunferência, calcule-a usando o comprimento do lado: p = 5s, onde s é o comprimento do lado.

2. Use o comprimento do lado. Se você souber apenas o comprimento dos lados, use a seguinte fórmula:

3. Escolha uma fórmula que use apenas o raio. Você pode até encontrar a área se souber apenas o raio. Use a seguinte fórmula:
Pontas
- Pentágonos irregulares ou pentágonos com lados desiguais são mais difíceis de estudar. A melhor abordagem geralmente é dividir o pentágono em triângulos e somar as áreas de todos os triângulos. Você também pode precisar desenhar uma forma maior ao redor do pentágono, calcular sua área e depois subtrair a área do espaço extra.
- Se possível, use um método geométrico e uma fórmula e compare os resultados para verificar sua resposta. As respostas podem ser um pouco diferentes quando você preenche a fórmula completamente de uma só vez (porque as etapas que você completa estão faltando), mas elas devem estar muito próximas.
- Os exemplos dados aqui usam valores arredondados para facilitar sua matemática. Se você tiver um polígono real com os comprimentos dos lados fornecidos, obterá resultados ligeiramente diferentes para os outros comprimentos e áreas.
- As fórmulas são derivadas de métodos geométricos, semelhantes aos descritos aqui. Tente descobrir como distraí-los você mesmo. A fórmula do raio é mais difícil de derivar do que as outras (dica: você precisa da identidade de ângulo duplo).
Artigos sobre o tópico "Calcular a área de um pentágono"
Оцените, пожалуйста статью
Popular