Calculando o Volume de um Cubo

Contente

Degraus

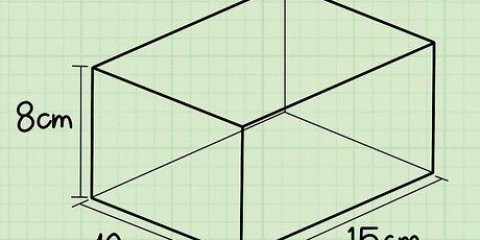
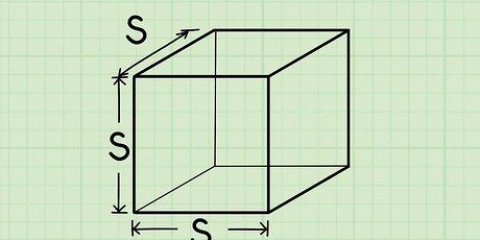
Um cubo é uma figura tridimensional cujo comprimento, largura e altura são iguais. Um cubo tem seis faces quadradas, cujos lados são de igual comprimento e perpendiculares entre si. Calcular o volume de um cubo é muito simples - geralmente você só precisa multiplicar o seguinte: comprimento × largura × altura. Como todas as arestas de um cubo têm o mesmo comprimento, você também pode ver o volume de um cubo da seguinte forma: eu, através do qual eu é o comprimento de uma das arestas do cubo. Vá para a etapa 1 para obter uma explicação detalhada.

Degraus

Método 1 de 3: Elevando a borda do cubo até o cubo

Imagem intitulada Calcular o Volume de um Cubo Passo 1

1. Encontre o comprimento de uma das arestas do cubo. Muitas vezes você verá uma soma onde o comprimento de uma das costelas já é dado. Depois de ter essas informações, você tem tudo o que precisa para determinar o volume do cubo. Use uma régua ou fita métrica se você não estiver resolvendo um problema de matemática, mas apenas quiser saber o volume de um objeto em forma de cubo existente.

Para entender melhor o processo de determinação do volume de um cubo, vamos começar com um exemplo de soma enquanto percorremos as etapas desta seção. Suponha que a aresta do cubo 2 cm longo é. Vamos usar essas informações na próxima etapa para determinar o volume do cubo.

Imagem intitulada Calcular o Volume de um Cubo Passo 2

2. Aumente o comprimento da costela para a terceira potência. Depois de ter o comprimento de uma das costelas, eleve esse número à terceira potência. Em outras palavras, multiplique o número duas vezes por ele mesmo. E se eu é o comprimento da costela, então você multiplica eu × eu × eu (ou de forma mais simples eu). O resultado é o volume do cubo.

Esse processo é basicamente o mesmo que calcular primeiro a área da base e depois multiplicar essa área pela altura do cubo (ou em outras palavras comprimento × largura × altura), pois a área da base é determinada multiplicando o comprimento pela largura. Como o comprimento, a largura e a altura de um cubo são iguais, podemos simplificar o processo elevando um desses valores à terceira potência.

Vamos continuar com nosso exemplo. O comprimento da aresta era de 2 cm, então o volume do cubo é 2 x 2 x 2 (ou 2) = 8.

Imagem intitulada Calcular o Volume de um Cubo Passo 3

3. Dê sua resposta em unidades cúbicas. O volume é a medida de um espaço tridimensional, então a solução deve ser escrita em unidades cúbicas. Em um teste, pode custar pontos se você não responder corretamente em unidades cúbicas, então não se esqueça!

No nosso exemplo, o comprimento da costela foi dado em centímetros, então a resposta deve ser dada em centímetros cúbicos. Então a resposta é 8 cm.

Método 2 de 3: Determinando o volume por área de superfície

Imagem intitulada Calcular o Volume de um Cubo Passo 4

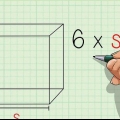
1. Encontre a área das faces do seu cubo. O mais fácil maneira de determinar o volume é elevando a costela ao cubo, mas não é o qualquer caminho. O comprimento da aresta de um cubo ou a área de uma de suas faces pode ser derivada de várias outras propriedades do cubo, o que significa que se você começar com essa informação poderá determinar o volume do cubo de forma derivada. Por exemplo, se você conhece apenas a área total de todos os lados do cubo, pode encontrar o volume dividindo essa área por seis e, em seguida, tirando a raiz quadrada desse número para encontrar o comprimento da aresta. A partir desse ponto, você pode elevar à terceira potência novamente. Nesta seção, percorremos esse processo passo a passo.

A área de um cubo é dada pela fórmula 6eu, através do qual eu é o comprimento de uma das arestas do cubo. Esta fórmula é na verdade o mesmo que determinar a área bidimensional de um dos lados do cubo e, em seguida, adicionar as seis áreas (iguais). Usaremos esta fórmula para determinar o volume do cubo a partir da área do cubo.
Suponha que temos um cubo do qual sabemos que a área 50 cm é, mas não sabemos qual é o comprimento das costelas. Nas próximas etapas, usaremos essas informações para encontrar o volume do cubo.

Imagem intitulada Calcular o Volume de um Cubo Passo 5

2. Divida a área do cubo por seis. Como o cubo tem seis faces de igual área, podemos determinar a área de uma face dividindo a área do cubo por seis. A área de um plano é o mesmo que a multiplicação de duas arestas (l × b, b × h, ou h × l).

Então, em nosso exemplo, dividimos cinquenta por seis: 50/6 = 8,33 centímetros. Lembre-se que as unidades das respostas bidimensionais são escritas ao quadrado (cm, m e assim por diante).

Imagem intitulada Calcular o Volume de um Cubo Passo 6

3. Encontre a raiz quadrada deste valor. Como a área de uma das faces de um cubo é igual a eu (eu × eu), agora podemos tirar a raiz quadrada do valor encontrado para determinar o comprimento de uma das costelas. Depois de saber isso, você terá informações suficientes para calcular o volume do cubo como de costume.

Em nosso exemplo, √8,33 = 2,89 centímetros.

Imagem intitulada Calcular o Volume de um Cubo Passo 7

4. Eleve este número à terceira potência para encontrar o volume do cubo. Agora que você determinou um valor para o comprimento das costelas, você pode aumentar esse número para o cubo para determinar o volume conforme descrito na primeira seção deste artigo.

Então, em nosso exemplo: 2,89 × 2,89 × 2,89 = 24,14 centímetros. Não se esqueça de escrever a resposta em unidades cúbicas.

Método 3 de 3: Determinando o volume usando diagonais

Imagem intitulada Calcular o Volume de um Cubo Passo 8

1. Divida a diagonal de uma das faces do cubo por √2 para encontrar o comprimento das arestas do cubo. A diagonal de um quadrado é √2 × o comprimento de uma de suas arestas. Em outras palavras, se você conhece apenas o valor de uma das diagonais de uma face do cubo, pode calcular o comprimento das arestas do cubo dividindo esse valor por √2. A partir desse ponto, você pode aumentar para a terceira potência novamente e determinar o volume conforme descrito acima.

Suponha que uma das faces do cubo tenha uma diagonal de7 metros grandes. Então podemos calcular o comprimento de uma das costelas dividindo 7 por √2. 7/√2 = 4,96 metros. Agora que sabemos o comprimento das arestas do cubo, podemos calcular o volume do cubo elevando 4,96 ao cubo: 4,96 = 122,36 metros.
Prestar atenção: d = 2eu, verdadeiro d é o comprimento da diagonal de uma das faces do cubo e eu é o comprimento de uma das arestas do cubo. Isso pode ser derivado do teorema de Pitágoras, onde o quadrado da hipotenusa de um triângulo equilátero é igual à soma do quadrado dos outros dois lados. Como a diagonal de uma face de um cubo forma um triângulo equilátero com duas das arestas dessa face, podemos dizer o seguinte: d = eu + eu = 2eu.

Imagem intitulada Calcular o Volume de um Cubo Passo 9

2. Encontre o quadrado da diagonal entre dois cantos opostos do cubo, divida por três e tire a raiz quadrada para encontrar o comprimento de uma das arestas. Se o comprimento da linha tridimensional entre dois cantos opostos do cubo for o único dado, você ainda poderá determinar o volume do cubo. d forma um dos lados de um triângulo equilátero cuja hipotenusa é a linha entre dois vértices opostos do cubo, então podemos dizer: d = 3eu, onde D é a linha tridimensional entre dois cantos opostos do cubo.

Isso também pode ser deduzido do teorema de Pitágoras. d, d e eu formam um triângulo equilátero com D como hipotenusa, então d = d + eu. Anteriormente já havíamos determinado: d = 2eu, então também podemos dizer o seguinte: d = 2eu + eu = 3eu.

Suponha que sabemos que o comprimento da diagonal que vai de um canto na base do cubo até o canto oposto na face superior do cubo é de 10 metros. Então, se quisermos calcular o volume, inserimos 10 na fórmula acima para d.

d = 3eu.

10 = 3eu.

100 = 3eu

33.33 = eu

5.77 m = l. A partir deste ponto, podemos calcular o volume elevando o comprimento da costela ao cubo.

5.77 = 192.45 m