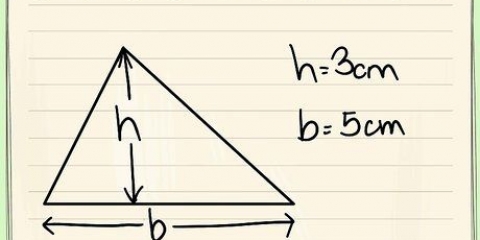
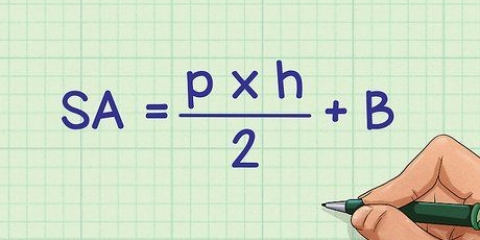Por exemplo, se um triângulo isósceles tem lados de 5 cm, 5 cm e 6 cm, então o lado de 6 cm é a base. Se um triângulo tem três lados iguais (e, portanto, é equilátero), então você pode escolher qualquer lado como base. Um triângulo equilátero é um tipo especial de triângulo isósceles, mas você pode encontrar sua área da mesma maneira. 
Em um triângulo isósceles, esta linha sempre toca a base em seu centro exato. 
Um dos lados curtos é igual a metade da base:  .
. O outro lado curto é a altura h. A hipotenusa (hipotenusa) do triângulo retângulo é um dos dois lados iguais do triângulo isósceles. Vamos pegar isso s mencionar. 
Você provavelmente aprendeu o teorema de Pitágoras se  . Escrever isso como `lados` e `hipotenusa` evita que você os confunda com as variáveis do triângulo.
. Escrever isso como `lados` e `hipotenusa` evita que você os confunda com as variáveis do triângulo. 


 .
.
Por exemplo, você tem um triângulo isósceles com lados 5 cm, 5 cm e 6 cm. b = 6 e s = 5. Use esses valores em sua fórmula:





 cm.
cm. 
Continuando com o exemplo: o triângulo 5-5-6 tem 6 cm de base e 4 cm de altura. A = bh
A = ½(6cm)(4cm)
A = 12cm. 
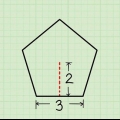
Qual é a área de um triângulo com lados 8 cm, 8 cm e 4 cm? O lado irregular é de 4 cm, e a base b. A altura 


Simplifique a raiz quadrada fatorando: 
Superfície 


Deixe esta resposta como anotada ou use uma calculadora para uma estimativa decimal (cerca de 15,49 cm2). 

Esta linha divide θ perfeitamente ao meio. Todo triângulo retângulo tem um ângulo de ½θ, ou neste caso (½)(120) = 60 graus. 
cos(θ/2) = h/s cos(60º) = h / 10 h = 10cos(60º) 
sin(θ/2) = x/s sin(60º) = x / 10 x = 10sin(60º) 





Usando uma calculadora (definida para graus), você obtém cerca de 43,3 cm2 como resposta. Alternativamente, use as propriedades da trigonometria para simplificá-las para A = 50sin(1200). 

s é o comprimento de um dos dois lados iguais. Θ é o ângulo entre os dois lados iguais.
Calcular a área de um triângulo isósceles
Contente
Um triângulo isósceles é um triângulo com dois lados de mesmo comprimento. Esses dois lados iguais sempre têm o mesmo ângulo com a base (o terceiro lado) e se encontram diretamente acima do centro da base. Você pode testar isso sozinho com uma régua e dois lápis de comprimento igual: se você tentar inclinar o triângulo em uma direção, as extremidades dos lápis não se encontrarão. Com essas propriedades especiais do triângulo isósceles, a área pode ser calculada com apenas alguns dados.
Degraus
Método 1 de 2: Determinando a área usando os comprimentos de cada lado

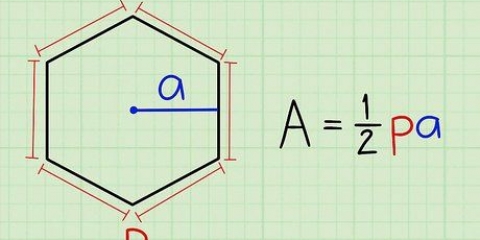
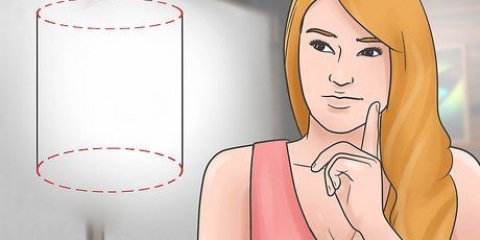
1. Pegue a área de um paralelogramo. Quadrados e retângulos são paralelogramos, como qualquer forma de quatro lados onde dois pares de lados são paralelos um ao outro. Todos os paralelogramos têm uma fórmula de área simples: a área é igual à base multiplicada pela altura, ou A = bh. Se você colocar um paralelogramo imaginário na vertical em uma superfície horizontal, a base é o comprimento do lado em que a figura está. A altura é a distância da base ao ponto mais alto (como seria de esperar); ou seja, a distância da base para o lado oposto. Sempre meça a altura em um ângulo reto (90 graus) em relação à base.
- Para quadrados e retângulos, a altura é igual ao comprimento de um lado vertical, pois esses lados são perpendiculares ao solo.

2. Comparar triângulos e paralelogramos. Existe uma relação simples entre essas duas formas. Cortar um paralelogramo ao meio ao longo da diagonal o divide em dois triângulos iguais. Da mesma forma, você pode juntar dois triângulos idênticos para formar um paralelogramo. Isso significa que a área de um triângulo pode ser escrita como A = bh, exatamente metade do tamanho de um paralelogramo correspondente.

3. Encontre a base do triângulo isósceles. Agora você tem a fórmula, mas o que exatamente são a `base` e a `altura` de um triângulo isósceles? A base é a parte fácil: basta pegar o terceiro lado desigual do triângulo isósceles.

4. Desenhe uma linha entre a base e o vértice oposto. Certifique-se de que a linha toca a base em um ângulo reto. O comprimento desta linha é a altura do triângulo e, portanto, é rotulado h. Depois de obter o valor de h calculado, você pode determinar a área.

5. Veja uma metade do triângulo isósceles. Observe que a altitude divide o triângulo isósceles em dois triângulos retângulos idênticos. Olhe para um deles e aponte para os três lados:
 .
.
6.Use o Teorema de Pitágoras. Se você conhece dois lados de um triângulo retângulo e deseja encontrar o terceiro, pode usar o Teorema de Pitágoras: (lado 1) + (lado 2) = (hipotenusa) Substitua as variáveis que usamos neste problema e você obtém  .
.
 .
. . Escrever isso como `lados` e `hipotenusa` evita que você os confunda com as variáveis do triângulo.
. Escrever isso como `lados` e `hipotenusa` evita que você os confunda com as variáveis do triângulo.
7. Resolva para h. Lembre-se que você tem a fórmula da área b e h usado, mas que você não sabe o valor de h não sei ainda. Reescreva a fórmula h resolver:


 .
.
8. Substitua os valores do seu triângulo por h Agora que você conhece esta fórmula, você pode usá-la para um triângulo isósceles cujos lados você conhece. Basta digitar o comprimento da base para b e o comprimento de um dos lados iguais para s, e calcule depois h.





 cm.
cm.
9. Use os valores de base e altura na fórmula da área. Agora você tem o que precisa para usar a fórmula do início desta seção: Área = ½ bh. Substitua os valores de b e h nesta fórmula e calcule a resposta. Não se esqueça de escrever sua resposta em unidades quadradas.
A = ½(6cm)(4cm)
A = 12cm.

10. Tente um exemplo mais difícil. A maioria dos triângulos isósceles são mais difíceis de trabalhar do que no exemplo anterior. Altura geralmente contém uma raiz quadrada que não pode ser simplificada para um número inteiro. Se este for o caso, deixe a altura como a raiz quadrada no forma mais simples ficar de pé. Aqui está um exemplo:







Método 2 de 2: usando trigonometria

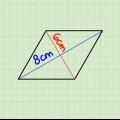
1. Comece com um lado e um canto. Se você estiver familiarizado com trigonometria, poderá encontrar a área de um triângulo isósceles, mesmo que nenhum dos comprimentos de seus lados seja conhecido. Aqui está um exemplo de problema onde apenas o seguinte é conhecido:
- O comprimento s dos dois lados iguais é 10 cm.
- O ângulo entre os dois lados iguais é de 120 graus.

2. Divida o triângulo isósceles em dois triângulos retângulos. Desenhe uma linha para baixo do vértice entre os dois lados iguais, cruzando a base em um ângulo reto. Agora você tem dois triângulos retângulos iguais.

3. Use trigonometria para determinar o valor de h. Agora que você tem um triângulo retângulo, você pode aplicar as funções trigonométricas (seno, cosseno e tangente). No problema de exemplo, você sabe o que é a hipotenusa e quer o valor de h sabe, o lado próximo ao ângulo conhecido. Use o fato de que cosseno = adjacente / hipotenusa para h resolver:

4. Determine o valor do lado restante. Há um lado ainda desconhecido do triângulo retângulo, que você X pode nomear. Resolva isso com a definição seno = oposto / hipotenusa:

5. Use a relação de x com a base do triângulo isósceles. Agora você pode diminuir o zoom para o triângulo isósceles em questão. A base b desse ângulo é igual a 2X, uma vez que foi dividido em dois segmentos, cada um com um comprimento X.

6. Utilize os valores h e b na fórmula da área do triângulo. Agora que você conhece a base e a altura, pode aplicar a fórmula padrão A = ½bh:





7. Reescreva isso como uma fórmula universal. Agora que você sabe como corrigir isso, você pode aplicar a fórmula geral sem passar por todo o processo toda vez. Aqui está o que você obtém se repetir esse processo, sem usar valores específicos (e simplificando usando as propriedades de trigonometria):

Pontas
- Se você está lidando com um triângulo retângulo isósceles (dois lados iguais e um ângulo de 90 graus), é muito mais fácil encontrar a área. Se você usar um dos lados curtos como base, o outro lado curto é a altura. Agora a fórmula A = ½ b * h pode ser simplificada para ½s, onde s é o comprimento de um lado curto.
- As raízes quadradas têm duas soluções, uma positiva e outra negativa, mas você pode ignorar o negativo na geometria. Por exemplo, você não pode ter um triângulo com uma `altura negativa`.
- Alguns problemas trigonométricos fornecem outras informações para começar, como o comprimento da base e um ângulo (e o fato de o triângulo ser isósceles). A estratégia básica permanece a mesma: divida o triângulo isósceles em triângulos retângulos e calcule a altura, usando funções trigonométricas.
Artigos sobre o tópico "Calcular a área de um triângulo isósceles"
Оцените, пожалуйста статью
Popular