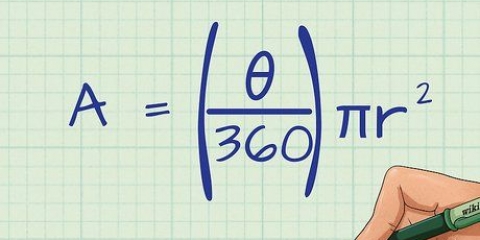Veja o apótema como o "x√3"-lado de um triângulo 30-60-90. Você pode ver assim porque o hexágono consiste em seis triângulos equiláteros. O apótema corta um desses triângulos ao meio, criando um triângulo com ângulos de 30, 60 e 90 graus. Você sabe que o lado oposto ao ângulo de 60 graus tem um comprimento de x√3, o lado oposto ao ângulo de 30 graus tem um comprimento de x, e o lado oposto ao ângulo de 90 graus tem um comprimento de 2x. Se 10√3 significa "x√3," então você sabe que x = 10. Você sabe que x é metade do comprimento da base do triângulo. Dobre isso para determinar o comprimento total. Então a base do triângulo é 20. Existem seis desses lados no hexágono, então para encontrar o perímetro do hexágono multiplicamos 20 por 6 = 120. 
Área = 1/2 x 120 x 10√3 Área = 60 x 10√3 Área = 600√3 


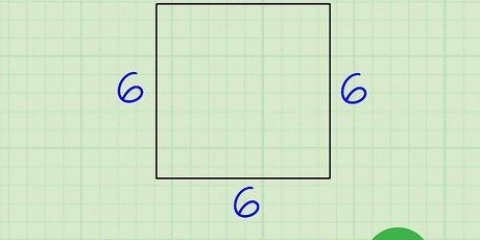
Se você tem um quadrado com lados de comprimento 6, então a área é 6 x 6 = 36. 
Se a base de um retângulo é 4 e a altura é 3, então a área é 4 x 3 = 12. 
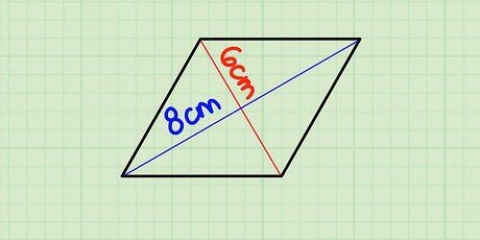
Suponha que você tenha um trapézio cujas bases têm comprimentos 6 e 8 e cuja altura é 10. Então a área é [(6 + 8) x 10]/2, que pode ser simplificada para (14 x 10)/2 ou 140/2, que é uma área de 70. 





Calcular a área de um polígono
Contente
Calcular a área de um polígono pode ser muito simples quando se trata de um triângulo regular. Mas fica muito mais difícil quando se trata de uma forma irregular com onze lados. Se você quiser saber como calcular a área de diferentes polígonos, siga estes passos.
Degraus
Parte 1 de 3: Calculando a área dos polígonos usando o apótema

1. Escreva a fórmula para encontrar a área de um polígono regular. Para encontrar a área de um polígono regular, basta seguir a fórmula: área = 1/2 x perímetro x apótema. Isso significa o seguinte:
- Circunferência = soma dos comprimentos de todos os lados
- Apothem = o segmento e também a distância do centro do polígono ao centro de um lado

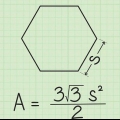
2. Determine o apótema do polígono. Se você usar o método apótema, o apótema será sempre um dado. Suponha que você esteja trabalhando com um hexágono cujo apótema tem um comprimento de 10√3.

3. Determine o perímetro do polígono. Se a circunferência é um dado, você está quase pronto. Mas provavelmente apenas o apótema é dado. Se você sabe que é um polígono regular, pode usar o apótema para determinar seu perímetro. É assim que você faz isso:

4. Agora podemos colocar o apótema e o perímetro na fórmula. De novo: área = 1/2 x perímetro x apótema, o perímetro é 120 e o apótema é 10√3. Então a fórmula fica assim:

5. Simplifique sua resposta. Talvez você deva escrever o resultado em decimais em vez de um radical. Use sua calculadora para encontrar a raiz quadrada aproximada de três e multiplique isso por 600. √3 x 600 = 1,039.2. Esse é o resultado em decimais.
Parte 2 de 3: Encontrando a área de um polígono regular usando outras fórmulas

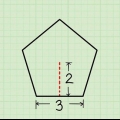
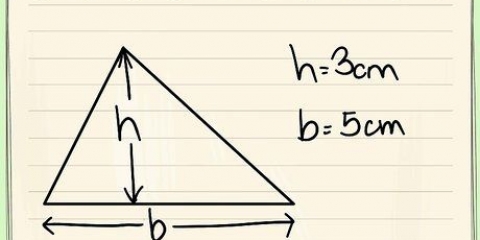
1. Calcular a área de um triângulo par. Se você deseja encontrar a área de um triângulo regular, pode usar esta fórmula: área = 1/2 x base x altura.
- Se você tem um triângulo com base 10 e altura 8, então a área = 1/2 x 8 x 10 = 40.

2. Calcular a área de um quadrado. Para encontrar a área de um quadrado basta multiplicar um de seus lados por ele mesmo, pois a base e a altura são iguais para um quadrado.

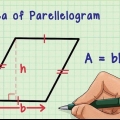
3. Calcular a área de um retângulo. Para encontrar a área de um retângulo tudo que você precisa fazer é multiplicar sua base pela sua altura.

4.Calcular a área de um trapézio. Para encontrar a área de um trapézio, você pode usar a seguinte fórmula: área = [(base 1 + base 2) x altura]/2.
Parte 3 de 3: Encontrando a área de um polígono irregular

1. Use as coordenadas dos nós para calcular a área. Se você conhece as coordenadas, pode calcular a área de um polígono irregular.

2. Crie uma sequência. Liste as coordenadas xey de cada vértice do polígono, no sentido anti-horário. Repita as coordenadas do primeiro ponto na parte inferior da lista.

3. Multiplique a coordenada x de cada vértice pela coordenada y do próximo vértice. Some os resultados. A soma desses produtos é 82.

4. Multiplique a coordenada y de cada vértice pela coordenada x do próximo vértice. Some os resultados. A soma desses produtos é -38.

5. Subtraia a soma dos produtos calculados na etapa 4 da soma dos produtos calculados na etapa 3. (82) - (-38) = 120.

6. Divida este resultado por 2 para encontrar a área do polígono. Área = 120/2 = 60.
Pontas
- Se você listar os pontos no sentido horário em vez do anti-horário, você também obterá a área, mas negativa. Por exemplo, você pode usar isso como uma ferramenta para determinar a sequência cíclica de um conjunto de pontos que formam um polígono.
- Esta fórmula calcula a área com orientação. Se você usá-lo em uma forma onde duas das linhas se cruzam como em um 8, você obtém a área no sentido anti-horário menos a área no sentido horário.
Artigos sobre o tópico "Calcular a área de um polígono"
Оцените, пожалуйста статью
Popular